Beam propagation method
Encyclopedia
Beam Propagation Method refers to a computational technique in Electromagnetics, used
to solve the Helmholtz equation
under conditions of a time-harmonic wave. BPM works under slowly varying envelope approximation
, for linear and nonlinear equations.
The beam propagation method (BPM) is an approximation technique for simulating the propagation of light
in slowly varying optical waveguide
s. It is essentially the same as the so-called Parabolic Equation (PE) method in underwater acoustics
. Both BPM and the PE were first introduced in the 1970s. When a wave propagates along a waveguide for a large distance (larger compared with the wavelength), rigorous numerical simulation is difficult. The BPM relies on approximate differential equations which are also called the one-way models. These one-way models involve only a first order derivative
in the variable z (for the waveguide axis) and they can be solved as "initial" value problem. The "initial" value problem does not involve time, rather it is for the spatial variable z.
The original BPM and PE were derived from the slowly varying envelope approximation and they are the so-called paraxial one-way models. Since then, a number of improved one-way models are introduced. They come from a one-way model involving a square root operator. They are obtained by applying rational approximations to the square root operator. After a one-way model is obtained, one still has to solve it by discretizing the variable z. However, it is possible to merge the two steps (rational approximation to the square root operator and discretization of z) into one step. Namely, one can find rational approximations to the so-called one-way propagator (the exponential of the square root operator) directly. The rational approximations are not trivial. Standard diagonal Padé approximants have trouble with the so-called evanescent modes. These evanescent modes should decay rapidly in z, but the diagonal Padé approximants will incorrectly propagate them as propagating modes along the waveguide. Modified rational approximants that can suppress the evanescent modes are now available. The accuracy of the BPM can be further improved, if you use the energy-conserving one-way model or the single-scatter one-way model.
in a time-harmonic case,
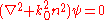
with the field written as,
.
Now the spatial dependence of this field is written according to any one TE or TM
polarizations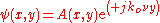
,
with the envelope
following a slowly varying approximation,
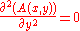
Now the solution when replaced into the Helmholtz equation follows,
With the aim to calculate the field at all points of space for all times, we only need to compute the function
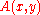for all space, and then we are able to reconstruct 
. Since the solution
is for the time-harmonic Helmholtz equation, we only need to calculate it over one time period. We can
visualize the fields along the propagation direction, or the cross section waveguide modes.
The master equation is discretized (using various centralized difference, Crank–Nicolson method etc.) and rearranged in a causal fashion. Through iteration the field evolution is computed, along the propagation
direction.
used only in solving for intensity and modes within shaped (bent, tapered, terminated) waveguide
structures, as opposed to scattering problems. These structures typically consist of isotropic optical materials, but the BPM has also been extended to be applicable to simulate the propagation of light in general anisotropic materials such as liquid crystals. This allows to analyze e.g. the polarization rotation of light in anisotropic materials, the tunability of a directional coupler based on liquid crystals or the light diffraction in LCD pixels.
to solve the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
under conditions of a time-harmonic wave. BPM works under slowly varying envelope approximation
Slowly varying envelope approximation
In physics, the slowly varying envelope approximation is the assumption that the envelope of a forward-travelling wave pulse varies slowly in time and space compared to a period or wavelength...
, for linear and nonlinear equations.
The beam propagation method (BPM) is an approximation technique for simulating the propagation of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
in slowly varying optical waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
s. It is essentially the same as the so-called Parabolic Equation (PE) method in underwater acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
. Both BPM and the PE were first introduced in the 1970s. When a wave propagates along a waveguide for a large distance (larger compared with the wavelength), rigorous numerical simulation is difficult. The BPM relies on approximate differential equations which are also called the one-way models. These one-way models involve only a first order derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
in the variable z (for the waveguide axis) and they can be solved as "initial" value problem. The "initial" value problem does not involve time, rather it is for the spatial variable z.
The original BPM and PE were derived from the slowly varying envelope approximation and they are the so-called paraxial one-way models. Since then, a number of improved one-way models are introduced. They come from a one-way model involving a square root operator. They are obtained by applying rational approximations to the square root operator. After a one-way model is obtained, one still has to solve it by discretizing the variable z. However, it is possible to merge the two steps (rational approximation to the square root operator and discretization of z) into one step. Namely, one can find rational approximations to the so-called one-way propagator (the exponential of the square root operator) directly. The rational approximations are not trivial. Standard diagonal Padé approximants have trouble with the so-called evanescent modes. These evanescent modes should decay rapidly in z, but the diagonal Padé approximants will incorrectly propagate them as propagating modes along the waveguide. Modified rational approximants that can suppress the evanescent modes are now available. The accuracy of the BPM can be further improved, if you use the energy-conserving one-way model or the single-scatter one-way model.
Principles
BPM is generally formulated as a solution to Helmholtz equationHelmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
in a time-harmonic case,
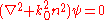
with the field written as,
.Now the spatial dependence of this field is written according to any one TE or TM
Transverse mode
A transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
polarizations
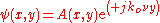,with the envelope
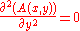
following a slowly varying approximation,Now the solution when replaced into the Helmholtz equation follows,
With the aim to calculate the field at all points of space for all times, we only need to compute the function
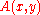for all space, and then we are able to reconstruct . Since the solutionis for the time-harmonic Helmholtz equation, we only need to calculate it over one time period. We can
visualize the fields along the propagation direction, or the cross section waveguide modes.
The master equation is discretized (using various centralized difference, Crank–Nicolson method etc.) and rearranged in a causal fashion. Through iteration the field evolution is computed, along the propagation
direction.
Applications
BPM is a quick and easy method of solving for fields in integrated optical devices. It is typicallyused only in solving for intensity and modes within shaped (bent, tapered, terminated) waveguide
structures, as opposed to scattering problems. These structures typically consist of isotropic optical materials, but the BPM has also been extended to be applicable to simulate the propagation of light in general anisotropic materials such as liquid crystals. This allows to analyze e.g. the polarization rotation of light in anisotropic materials, the tunability of a directional coupler based on liquid crystals or the light diffraction in LCD pixels.
BPM software
- RSoft's BeamPROP: vector; commercial, free trial possible
- Optiwave's OptiBPM: commercial, free trial possible
- FEAB (Finite Element Anisotropic Beam propagation method): academic, free version available
See also
- Computational electromagneticsComputational electromagneticsComputational electromagnetics, computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment....
- Finite-difference time-domain methodFinite-difference time-domain methodFinite-difference time-domain is one of the primary available computational electrodynamics modeling techniques. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.The FDTD method...
- Eigenmode expansionEigenmode expansionEigenmode Expansion is a computational electrodynamics modelling technique. It is also referred to as the mode matching technique or the Bidirectional Eigenmode Propagation method...
- Finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Method of LinesMol-Places:* City Municipality of Ljubljana, known after the acronym MOL in Slovene language * Märkisch-Oderland, a rural district of Brandenburg, Germany* Mol, Belgium, a municipality in Belgium* Mol, Serbia, a town in Serbia...
- LightLightLight or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
- PhotonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...