
Banach function algebra
Encyclopedia
In functional analysis
a Banach function algebra on a compact
Hausdorff space
X is unital subalgebra
, A of the commutative C*-algebra C(X) of all continuous
, complex
valued functions from X, together with a norm on A which makes it a Banach algebra
.
For every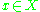 define
define 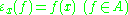 . Then
. Then 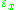
is a non-zero homomorphism (character) on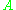 .
.
Theorem: A Banach function algebra is semisimple
(that is its Jacobson radical
is equal to zero) and each commutative unital, semisimple Banach algebra is isomorphic (via the Gelfand transform) to a Banach function algebra on its character space (the space of algebra homomorphisms from A into the complex numbers given the relative weak* topology).
If the norm on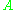 is the uniform norm (or sup-norm) on
is the uniform norm (or sup-norm) on 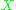 , then
, then  is called
is called
a uniform algebra. Uniform algebras are an important special case of Banach function algebras.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
a Banach function algebra on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
X is unital subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
, A of the commutative C*-algebra C(X) of all continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
valued functions from X, together with a norm on A which makes it a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
.
For every
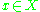 define
define 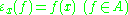 . Then
. Then 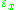
is a non-zero homomorphism (character) on
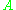 .
.Theorem: A Banach function algebra is semisimple
Semisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
(that is its Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
is equal to zero) and each commutative unital, semisimple Banach algebra is isomorphic (via the Gelfand transform) to a Banach function algebra on its character space (the space of algebra homomorphisms from A into the complex numbers given the relative weak* topology).
If the norm on
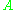 is the uniform norm (or sup-norm) on
is the uniform norm (or sup-norm) on 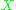 , then
, then  is called
is calleda uniform algebra. Uniform algebras are an important special case of Banach function algebras.

