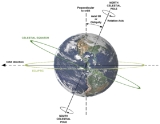
|
|
|
|
Axial tilt
|
| |
|
| |
In astronomy, axial tilt is the inclination angle of a planet's rotational axis in relation to a perpendicular to its orbital plane. It is also called axial inclination or obliquity. The axial tilt is expressed as the angle made by the planet's axis and a line drawn through the planet's center perpendicular to the orbital plane.
Obliquity
The axial tilt may equivalently be expressed in terms of the planet's orbital plane and a plane perpendicular to its axis. In our solar system, the Earth's orbital plane is known as the ecliptic, and so the Earth's axial tilt is officially called the obliquity of the ecliptic. In formulae it is abbreviated with the Greek letter e (Epsilon).
The Earth has an axial tilt of about 23.44° (23° 26’). The axis is tilted in the same direction throughout a year; however, as the Earth orbits the Sun, the hemisphere (half part of earth) tilted away from the Sun will gradually become tilted towards the Sun, and vice versa. This effect is the main cause of the seasons (see effect of sun angle on climate). Whichever hemisphere is currently tilted toward the Sun experiences more hours of sunlight each day, and the sunlight at midday also strikes the ground at an angle nearer the vertical and thus delivers more energy per unit surface area.
Lower obliquity causes polar regions to receive less solar radiation, producing conditions more favorable to glaciation. Like changes in precession and eccentricity, changes in tilt influence the relative strength of the seasons, but the effects of the tilt cycle are particularly pronounced in the high latitudes where the great ice ages began . Obliquity is a major factor in glacial/interglacial fluctuations (see Milankovitch cycles).
The obliquity of the ecliptic is not a fixed quantity but changing over time. It is a very slow effect known as nutation, and at the level of accuracy at which astronomers work, does need to be taken into account on a daily basis. Note that the obliquity and the precession of the equinoxes are calculated from the same theory and are thus related to each other. A smaller e means a larger p (precession in longitude) and vice versa. Yet the two movements act independent from each other, going in mutually perpendicular directions.
MeasurementKnowledge of the obliquity of the ecliptic (e) is critical for astronomical calculations and observations from the surface of the earth (earth-based, positional astronomy).
To quickly grasp an idea of its numerical value one can look at how the sun's angle above the horizon varies with the seasons; this was the way the Chinese astronomers determined it in 1000 BC. They measured the difference between the angles of the Sun above the horizon at noon on the longest and shortest days of the year. That difference in the angles is twice the obliquity.
The extreme northern and southern declination of the Sun during the year are equal to the obliquity. On the longest day of the year the earth is tilted toward the sun and we say that the sun's declination is + 23° 26’. To an observer on the equator standing all year long looking above, the sun will be directly overhead at noon in March, then swing north until it is e degrees away from the zenith in June. In September it will be back overhead, then at the Winter Solstice in December it will be e degrees away from the vertical again.
Example: an observer at 50° latitude (either north or south) will see the Sun 63° 26’ above the horizon at noon on the longest day of the year, but only 16° 34’ the shortest day. The difference is 2e = 46° 52’, and so e = 23° 26’.
(90° - 50°) + 23.4394° = 63.4394° when measuring angles from the horizon
(90° - 50°) - 23.4394° = 16.5606°
At the equator, this would be 90° + 23.4394° = 113.4394° and 90° - 23.4394° = 66.5606° (measuring always from the southern horizon).
Values
The Earth's axial tilt varies between 22.1° and 24.5° (but see below), with a 41,000-year period, and at present, the tilt is decreasing. In addition to this steady decrease, there are also much smaller short term (18.6 years) variations, known as nutation.
Simon Newcomb's calculation at the end of the nineteenth century for the obliquity of the ecliptic gave a value of 23° 27’ 8.26” (epoch of 1900), and this was generally accepted until improved telescopes allowed more accurate observations, and electronic computers permitted more elaborate models to be calculated. Lieske came with an updated model in 1976 with e equal to 23° 26’ 21.448” (epoch of 2000), which is part of the approximation formula recommended by the International Astronomical Union in 2000:
e = 84,381.448 - 46.84024T - (59 × 10-5)T² + (1,813 × 10-6)T³, measured in seconds of arc, with T being the time in Julian centuries (that is, 36,525 days) since the ephemeris epoch of 2000 (which occurred on Julian day 2,451,545.0). A straight application of this formula to 1900 (T=-1) returns Newcomb's value.
With the linear term in T being negative, at present the obliquity is slowly decreasing. It is implicit that this expression gives only an approximate value for e and is only valid for a certain range of values of T. If not, e would approach infinity as T approaches infinity. Computations based on a numerical model of solar system show that e has a period of about 41,000 years, the same as the constants of the precession of the equinoxes (although not of the precession itself).
Other theoretical models may come with values for e expressed with higher powers of T, but since no (finite) polynomial can ever represent a periodic function, they all go to either positive or negative infinity for large enough T. In that respect one can understand the decision of the International Astronomical Union to choose the simplest equation which agrees with most models. For up to 5,000 years in the past and the future all formulas agree, and up to 9,000 years in the past and the future, most agree to reasonable accuracy. For eras farther out discrepanies get too large.
Long period variationsNevertheless extrapolation of the average polynomials gives a fit to a sine curve with a period of 41,013 years, which, according to Wittmann, is equal to:
e = A + B sin (C(T + D)), with A = 23.496932° ± 0.001200°, B = - 0.860° ± 0.005°, C = 0.01532 ± 0.0009 radians/Julian century, D = 4.40 ± 0.10 Julian centuries, and T, the time in centuries from the epoch of 2000 as above.
This means a range of the obliquity from 22° 38’ to 24° 21’, the last maximum was reached in 8700 BC, the mean value occurred around 1550 and the next minimum will be in 11800. This formula should give a reasonable approximation for the previous and next million years or so. Yet it remains an approximation in which the amplitude of the wave remains the same, while in reality, as seen from the results of the Milankovitch cycles, irregular variations occur. The quoted range for the obliquity is from 21° 30’ to 24° 30’, but the low value may have been a one-time overshot of the normal 22° 30’.
If we go back over the last 5 million years, the obliquity of the ecliptic (or more accurately, the obliquity of the equator on the moving ecliptic of date) has varied from 22.0425° to 24.5044°. But for the next one million years the range will be only from 22.2289° to 24.3472°.
Other planets may have a variable obliquity too, for example on Mars the range is believed to be between 15° and 35°, as a result of gravitational perturbations from other planets . The relatively small range for the Earth is due to the stabilizing influence of the Moon, but it will not remain so. According to Ward, the orbit of the Moon (which is continuously increasing due to tidal effects) will have gone from the current 60 to approximately 66.5 Earth radii in about 1.5 billion years. Once this occurs, a resonance from planetary effects will follow, causing swings of the obliquity between 22° and 38°. Further, in approximately 2 billion years, when the Moon reaches a distance of 68 Earth radii, another resonance will cause even greater oscillations, between 27° and 60°. This would have extreme effects on climate.
Tentative evidence has recently emerged for extreme (> 50°) variations in terrestrial axial tilt
Axial tilt of major celestial bodies
See also
External links - by Jeff Bryant, The Wolfram Demonstrations Project.
|
| |
|
|
