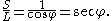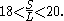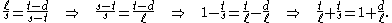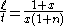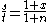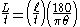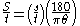Aristarchus On the Sizes and Distances
Encyclopedia
Aristarchus of Samos
Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe...
, an ancient Greek astronomer who flourished circa 280–240 BC. This work calculates the sizes of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
and Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, as well as their distances from the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
in terms of Earth's radius.
However, since the time of Voltaire, questions have existed as to whether the work is genuinely Aristarchos'. In 2009, it was revealed (DIO 14 ‡2 §C pp.18-25) that misunderstanding the ancient angular unit "meros" appears to have introduced an error by a factor of 4 into several calculations, which explains the work's bizarre demands that central lunar eclipses last ½ a day, and that the Moon retrogrades against the stars every day. The testimony of Archimedes indeed disagrees on the solar diameter by a factor of 4. In 2011, it was first pointed out that the work's best-known data, its 87° half-Moon solar elongation-limit and 2° solar diameter, are mathematically incompatible with each other, given the precision of human vision.
Symbols
The work's method relied on several observations:- The apparent size of the Sun and the Moon in the sky
- The size of the Earth's shadow in relation to the Moon during a lunar eclipseLunar eclipseA lunar eclipse occurs when the Moon passes behind the Earth so that the Earth blocks the Sun's rays from striking the Moon. This can occur only when the Sun, Earth, and Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, a lunar eclipse can only occur the night of a...
- The angle between the Sun and Moon during a half moonHalf MoonHalf Moon is a lunar phase coinciding with neap tides, which are often easier for seafarers than spring tides. This would apply to the first quarter and last quarter moon; in both cases, half of the moon's disk is lit...
is very close to 90°.
The rest of the article details a reconstruction of Aristarchus' method and results. The reconstruction uses the following variables:
| Symbol | Meaning |
|---|---|
| φ | Angle between the Earth and the Sun during a half moon (directly measurable) |
| L | Distance to the Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more... |
| S | Distance to the Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... |
| ℓ | Radius of the Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more... |
| s | Radius of the Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... |
| t | Radius of the Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets... |
| D | Distance from the center of Earth to the vertex of Earth's shadow cone |
| d | Radius of the Earth's shadow at the location of the Moon |
| n | Ratio, d/ℓ (a directly observable quantity during a lunar eclipse Lunar eclipse A lunar eclipse occurs when the Moon passes behind the Earth so that the Earth blocks the Sun's rays from striking the Moon. This can occur only when the Sun, Earth, and Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, a lunar eclipse can only occur the night of a... ) |
| x | Ratio, S/L = s/ℓ (which is calculated from φ) |
Half Moon
Aristarchus began with the premise that, during a half moonHalf Moon
Half Moon is a lunar phase coinciding with neap tides, which are often easier for seafarers than spring tides. This would apply to the first quarter and last quarter moon; in both cases, half of the moon's disk is lit...
, the moon forms a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
with the Sun and Earth. By observing the angle between the Sun and Earth, φ, the ratio of the distances to the Sun and Moon could be deduced using a form of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
.
From the diagram and trigonometry, we can calculate that
The diagram is greatly exaggerated, because in reality, S = 390 L, and φ is extremely close to 90°. Aristarchus determined φ to be a thirtieth of a quadrant (in modern terms, 3°) less than a right angle: in current terminology, 87°. Trigonometric functions had not yet been invented, but using geometrical analysis in the style of Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, Aristarchus determined that
In other words, the distance to the Sun was somewhere between 18 and 20 times greater than the distance to the Moon. This value (or values close to it) was accepted by astronomers for the next two thousand years, until the invention of the telescope permitted a more precise estimate of solar parallax.
Aristarchus also reasoned that as the angular size of the Sun and the Moon were the same, but the distance to the Sun was between 18 and 20 times further than the Moon, the Sun must therefore be 18-20 times larger.
Lunar eclipse
Aristarchus then used another construction based on a lunar eclipse:By similarity of the triangles,
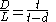and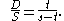 
Dividing these two equations and using the observation that the apparent sizes of the Sun and Moon are the same,
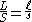, yields
The rightmost equation can either be solved for ℓ/t
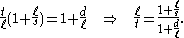
or s/t
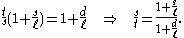
The appearance of these equations can be simplified using n = d/ℓ and x = s/ℓ.
The above equations give the radii of the Moon and Sun entirely in terms of observable quantities.
The following formulae give the distances to the Sun and Moon in terrestrial units:
where θ is the apparent radius of the Moon and Sun measured in degrees.
It is unlikely that Aristarchus used these exact formulae, since he would have lacked a precise value for π. However a simple approximation π = 3 will incur in a relative error smaller than 5%, well below experimental errors in measurements at the time.
These formulae are likely a good approximation to those of Aristarchus.
Results
The above formulae can be used to reconstruct the results of Aristarchus. The following table shows the results of a reconstruction using n = 2, x = 19.1 (φ = 87°) and θ = 1°, alongside the modern day accepted values.| Quantity | Reconstruction | Modern |
|---|---|---|
| s/t | 6.7 | 109 |
| t/ℓ | 2.85 | 3.50 |
| L/t | 20 | 60.32 |
| S/t | 380 | 23,500 |
The error in this calculation comes primarily from the poor values for x and θ. The poor value for θ is especially surprising, since Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
writes that Aristarchus was the first to determine that the Sun and Moon had an apparent diameter of half a degree. This would give a value of θ = 0.25, and a corresponding distance to the moon of 80 Earth radii, a much better estimate. The disagreement of the work with Archimedes seems to be due to its taking an Aristarchos statement that the lunisolar diameter is 1/15 of a "meros" of the zodiac to mean 1/15 of a zodiacal sign (30°), unaware that the Greek word "meros" meant either "portion" or 7°1/2; and 1/15 of the latter amount is 1°/2, in agreement with Archimedes' testimony.
A similar procedure
Hipparchus On Sizes and Distances
On Sizes and Distances [of the Sun and Moon] is a text by the ancient Greek astronomer Hipparchus. It is not extant, but some of its contents have been preserved in the works of Ptolemy and his commentator Pappus of Alexandria...
was later used by Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
, who estimated the mean distance to the moon as 67 Earth radii, and Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
, who took 59 Earth radii for this value.
Illustrations
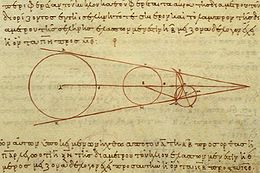
Some interactive illustrations of the propositions in On Sizes can be found here:- Proposition 1 states that 'two equal spheres are comprehended by one and the same cylinder, and two unequal spheres by one and the same cone which has its vertex in the direction of the lesser sphere; and the straight line drawn through the centres of the spheres is at right angles to each of the circles in which the surface of the cylinder, or of the cone, touches the spheres' (Heath 1913:354).
- Proposition 2 states that 'if a sphere be illuminated by a sphere greater than itself, the illuminated portion of the former sphere will be greater than a hemisphere' (Heath 1913:358).
- Proposition 3 states that 'the circle in the moon which divides the dark and the bright portions is least when the cone comprehending both the sun and the moon has its vertex at our eye' (Heath 1913:362).
- Proposition 4 states that 'the circle which divides the dark and the bright portions in the moon is not perceptibly different from a great circle in the moon' (Heath 1913:365).
- Proposition 6 states that 'the moon moves [in an orbit] lower than [that of] the sun, and, when it is halved, is distant less than a quadrant from the sun' (Heath 1913:372).
- Proposition 7 states that 'the distance of the sun from the earth is greater than 18 times, but less than 20 times, the distance of the moon from the earth' (Heath 1913:377). In other words, the sun is 18 to 20 times farther away and wider than the moon.
- Proposition 13 states that 'the straight line subtending the portion intercepted within the earth's shadow of the circumference of the circle in which the extremities of the diameter of the circle dividing the dark and the bright portions in the moon move is less than double of the diameter of the moon, but has to it a ratio greater than that which 88 has to 45; and it is less than 1/9th part of the diameter of the sun, but has to it a ratio greater than that which 21 has to 225. But it has to the straight line drawn from the centre of the sun at right angles to the axis and meeting the sides of the cone a ratio greater than that which 979 has to 10 125' (Heath 1913:394).
- Proposition 14 states that 'the straight line joined from the centre of the earth to the centre of the moon has to the straight line cut off from the axis towards the centre of the moon by the straight line subtending the [circumference] within the earth's shadow a ratio greater than that which 675 has to 1' (Heath 1913:400).
- Proposition 15 states that 'the diameter of the sun has to the diameter of the earth a ratio greater than 19/3, but less than 43/6' (Heath 1913:403). This means that the sun is (a mean of) 6¾ times wider than the earth, or that the sun is 13½ earth-radii wide. The moon and sun must then be 20¼ and 387 earth-radii away from us in order to subtend an angular size of 2º.
- Proposition 17a in al-Tusi's medieval Arabic version of the book On Sizes states that 'the ratio of the distance of the vertex of the shadow cone from the center of the moon (when the moon is on the axis [that is, at the middle of an eclipse] of the cone containing the earth and the sun) to the distance of the center of the moon from the center of the earth is greater than the ratio 71 to 37 and less than the ratio 3 to one' (Berggren & Sidoli 2007:218). In other words, that the tip of the earth’s shadow cone is between 108/37 and 4 times farther away than the moon.
Works cited
- Heath, T. L.. Aristarchus of Samos. Oxford, 1913. This was later reprinted, see (ISBN 0-486-43886-4).
- van Helden, A. Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. Chicago: Univ. of Chicago Pr., 1985. ISBN 0-226-84882-5.