
Antiunitary
Encyclopedia
In mathematics
, an antiunitary transformation, is a bijective antilinear map
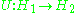
between two complex
Hilbert spaces such that
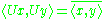
for all and
and  in
in 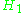 , where the horizontal bar represents the complex conjugate
, where the horizontal bar represents the complex conjugate
. If additionally one has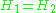 then U is called an antiunitary operator.
then U is called an antiunitary operator.
Antiunitary operators are important in Quantum Theory because they are used to represent certain symmetries, such as time-reversal symmetry. Their fundamental importance in quantum physics is further demonstrated by Wigner's Theorem
.
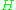 leave the absolute value of scalar product invariant:
leave the absolute value of scalar product invariant:
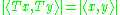
for all and
and 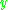 in
in 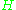 .
.
Due to Wigner's Theorem
these transformations fall into two categories, they can be unitary
or antiunitary.
of the plane form two distinguish classes. The first conserves the orientation and is generated by translations and rotations. The second does not conserve the orientation and is obtained from the first class by applying a reflection. On the complex plane these two classes corresponds (up to translation) to unitaries and antiunitaries, respectively.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an antiunitary transformation, is a bijective antilinear map
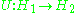
between two complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Hilbert spaces such that
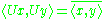
for all
 and
and 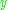 in
in 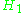 , where the horizontal bar represents the complex conjugate
, where the horizontal bar represents the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
. If additionally one has
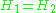 then U is called an antiunitary operator.
then U is called an antiunitary operator.Antiunitary operators are important in Quantum Theory because they are used to represent certain symmetries, such as time-reversal symmetry. Their fundamental importance in quantum physics is further demonstrated by Wigner's Theorem
Wigner's theorem
Wigner's theorem, proved by Eugene Wigner in 1931, is a cornerstone of the mathematical formulation of quantum mechanics. The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states....
.
Invariance transformations
In Quantum mechanics, the invariance transformations of complex Hilbert space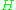 leave the absolute value of scalar product invariant:
leave the absolute value of scalar product invariant: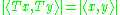
for all
 and
and 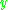 in
in 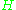 .
.Due to Wigner's Theorem
Wigner's theorem
Wigner's theorem, proved by Eugene Wigner in 1931, is a cornerstone of the mathematical formulation of quantum mechanics. The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states....
these transformations fall into two categories, they can be unitary
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
or antiunitary.
Geometric Interpretation
CongruencesCongruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
of the plane form two distinguish classes. The first conserves the orientation and is generated by translations and rotations. The second does not conserve the orientation and is obtained from the first class by applying a reflection. On the complex plane these two classes corresponds (up to translation) to unitaries and antiunitaries, respectively.
Properties
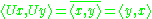 holds for all elements
holds for all elements 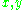 of the Hilbert space and an antiunitary
of the Hilbert space and an antiunitary  .
.- When
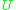 is antiunitary then
is antiunitary then 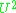 is unitary. This follows from
is unitary. This follows from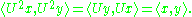
- For unitary operator
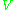 the operator
the operator 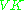 , where
, where 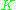 is complex conjugate operator, is antiunitary. The reverse is also true, for antiunitary
is complex conjugate operator, is antiunitary. The reverse is also true, for antiunitary 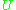 the operator
the operator 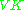 is unitary.
is unitary. - For antiunitary
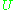 the adjoint operator
the adjoint operator 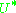 is also antiunitary and
is also antiunitary and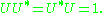
Examples
- The complex conjugate operator
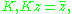 is an antiunitary operator on the complex plane.
is an antiunitary operator on the complex plane. - The operator

where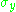 is the second Pauli matrixPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
is the second Pauli matrixPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
and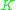 is the complex conjugate operator, is an antiunitary. It satisfies
is the complex conjugate operator, is an antiunitary. It satisfies  .
.
Decomposition of an antiunitary operator into a direct sum of elementary Wigner antiunitaries
An antiunitary operator on a finite-dimensional space may be decomposed as a direct sum of elementary Wigner antiunitaries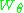 ,
,  . The operator
. The operator 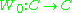 is just simple complex conjugation on C
is just simple complex conjugation on C
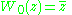
For , the operation
, the operation 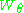 acts on two-dimensional complex Hilbert space. It is defined by
acts on two-dimensional complex Hilbert space. It is defined by
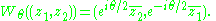
Note that for
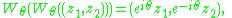
so such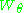 may not be further decomposed into
may not be further decomposed into 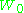 's, which square to the identity map.
's, which square to the identity map.
Note that the above decomposition of antiunitary operators contrasts with the spectral decomposition of unitary operators. In particular, a unitary operator on a complex Hilbert space may be decomposed into a direct sum of unitaries acting on 1-dimensional complex spaces (eigenspaces), but an antiunitary operator may only be decomposed into a direct sum of elementary operators on 1 and 2 dimensional complex spaces.
See also
- Unitary operatorUnitary operatorIn functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
- Wigner's TheoremWigner's theoremWigner's theorem, proved by Eugene Wigner in 1931, is a cornerstone of the mathematical formulation of quantum mechanics. The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states....
- Particle physics and representation theoryParticle physics and representation theoryIn physics, the connection between particle physics and representation theory is a natural connection, first noted by Eugene Wigner, between the properties of elementary particles and the representation theory of Lie groups and Lie algebras...
- Unitary operator

