
Particle physics and representation theory
Encyclopedia
In physics
, the connection between particle physics and representation theory is a natural connection, first noted by Eugene Wigner, between the properties of elementary particle
s and the representation theory
of Lie groups and Lie algebras. According to this connection, the different quantum states of an elementary particle give rise to an irreducible representation of the Poincaré group
. Moreover, the properties of the various particles, including their spectra, can be related to representations of Lie algebras, algebras corresponding to "approximate symmetries" of the universe.
, any particular particle (with a given momentum distribution, location distribution, spin state, etc.) is written as a vector
(or "ket
") in a Hilbert space
H. To help understand what types of particles can exist, it is important to classify the possibilities for H, and their properties. The particle is more precisely characterized by the associated projective
Hilbert space PH, since two vectors that differ by a scalar factor (or in physics terminology, two "kets" that differ by a "phase factor
") correspond to the same physical quantum state.
Let G be the symmetry group of the universe – that is, the set of symmetries under which the laws of physics are invariant. (For example, one element of G is the simultaneous translation of all particles and fields forward in time by five seconds.) Starting with a particular particle in the state ket , and a symmetry transformation g in G, it is possible to apply the symmetry transformation to the particle to get a new state ket
, and a symmetry transformation g in G, it is possible to apply the symmetry transformation to the particle to get a new state ket 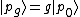 . For this picture to be consistent, it is necessary that PH is a projective group representation
. For this picture to be consistent, it is necessary that PH is a projective group representation
of G. (For example, this condition guarantees that applying a symmetry transformation, then applying its inverse transformation, will restore the original quantum state.)
Therefore, any given particle is associated with a unique representation
of G on a projective vector space PH. (We say the particle "lies in", or "transforms as" the representation.) In many important cases, it can be shown that the particle is also (more specifically) associated with a group representation
of G on the underlying (non-projective) space H. Wigner's Theorem
proves that it is a unitary representation
, or possibly anti-unitary.
So we conclude that each type of particle corresponds to a representation of G, and if we can classify the group representations of G, we will have much more information about the possibilities and properties of H, and hence what types of particles can exist.
, and this group is certainly a subgroup of G (neglecting general relativity
effects, or in other words, in flat space). Hence, any representation of G will in particular be a representation of the Poincaré group. Representations of the Poincaré group
are in many cases characterized by a nonnegative mass
and a half-integer spin
(see Wigner's classification
); this can be thought of as the reason that particles have quantized spin. (Note that there are in fact other possible representations, such as tachyon
s, infraparticle
s, etc., which in some cases do not have quantized spin or fixed mass.)
in the Poincaré group are particularly easy to visualize and believe, there are also other types of symmetries, called internal symmetries. One example is color
SU(3), an exact symmetry corresponding to the continuous interchange of the three quark
colors.
and independently by Yuval Ne'eman
(see the eightfold way
).
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the connection between particle physics and representation theory is a natural connection, first noted by Eugene Wigner, between the properties of elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s and the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of Lie groups and Lie algebras. According to this connection, the different quantum states of an elementary particle give rise to an irreducible representation of the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
. Moreover, the properties of the various particles, including their spectra, can be related to representations of Lie algebras, algebras corresponding to "approximate symmetries" of the universe.
General picture
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, any particular particle (with a given momentum distribution, location distribution, spin state, etc.) is written as a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(or "ket
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
") in a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H. To help understand what types of particles can exist, it is important to classify the possibilities for H, and their properties. The particle is more precisely characterized by the associated projective
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Hilbert space PH, since two vectors that differ by a scalar factor (or in physics terminology, two "kets" that differ by a "phase factor
Phase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
") correspond to the same physical quantum state.
Let G be the symmetry group of the universe – that is, the set of symmetries under which the laws of physics are invariant. (For example, one element of G is the simultaneous translation of all particles and fields forward in time by five seconds.) Starting with a particular particle in the state ket
 , and a symmetry transformation g in G, it is possible to apply the symmetry transformation to the particle to get a new state ket
, and a symmetry transformation g in G, it is possible to apply the symmetry transformation to the particle to get a new state ket 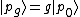 . For this picture to be consistent, it is necessary that PH is a projective group representation
. For this picture to be consistent, it is necessary that PH is a projective group representationProjective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
of G. (For example, this condition guarantees that applying a symmetry transformation, then applying its inverse transformation, will restore the original quantum state.)
Therefore, any given particle is associated with a unique representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
of G on a projective vector space PH. (We say the particle "lies in", or "transforms as" the representation.) In many important cases, it can be shown that the particle is also (more specifically) associated with a group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G on the underlying (non-projective) space H. Wigner's Theorem
Wigner's theorem
Wigner's theorem, proved by Eugene Wigner in 1931, is a cornerstone of the mathematical formulation of quantum mechanics. The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states....
proves that it is a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
, or possibly anti-unitary.
So we conclude that each type of particle corresponds to a representation of G, and if we can classify the group representations of G, we will have much more information about the possibilities and properties of H, and hence what types of particles can exist.
Poincaré group
The group of translations and Lorentz transformations form the Poincaré groupPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
, and this group is certainly a subgroup of G (neglecting general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
effects, or in other words, in flat space). Hence, any representation of G will in particular be a representation of the Poincaré group. Representations of the Poincaré group
Representation theory of the Poincaré group
In mathematics, the representation theory of the Poincaré group is an example of the representation theory of a Lie group that is neither a compact group nor a semisimple group. It is fundamental in theoretical physics....
are in many cases characterized by a nonnegative mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and a half-integer spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
(see Wigner's classification
Wigner's classification
In mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...
); this can be thought of as the reason that particles have quantized spin. (Note that there are in fact other possible representations, such as tachyon
Tachyon
A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...
s, infraparticle
Infraparticle
An infraparticle is an electrically charged particle and its surrounding cloud of soft photons—of which there are infinite number, by virtue of the infrared divergence of quantum electrodynamics. That is, it is a dressed particle rather than a bare particle...
s, etc., which in some cases do not have quantized spin or fixed mass.)
Other symmetries
While the spacetime symmetriesSpacetime symmetries
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...
in the Poincaré group are particularly easy to visualize and believe, there are also other types of symmetries, called internal symmetries. One example is color
Color charge
In particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
SU(3), an exact symmetry corresponding to the continuous interchange of the three quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
colors.
Approximate symmetries
Although the above symmetries are believed to be exact, other symmetries are only approximate.Hypothetical example
As an example of what an approximate symmetry means, suppose we lived inside an infinite ferromagnet, with magnetization in some particular direction. An experimentalist in this situation would find not one but two distinct types of electrons: one with spin along the direction of the magnetization, with a slightly lower energy (and consequently, a lower mass), and one with spin anti-aligned, with a higher mass. Our usual SO(3) rotational symmetry, which ordinarily connects the spin-up electron with the spin-down electron, has in this hypothetical case become only an approximate symmetry, relating different types of particles to each other.Lie algebras versus Lie groups
Many (but not all) symmetries or approximate symmetries, for example the ones above, form Lie groups. Rather than study the representation theory of these Lie groups, it is often preferable to study the closely related representation theory of the corresponding Lie algebras, which are usually simpler to compute.General definition
In general, an approximate symmetry arises when there are very strong interactions that obey that symmetry, along with weaker interactions that do not. In the electron example above, the two "types" of electrons behave identically under the strong and weak forces, but differently under the electromagnetic force.Example: flavour symmetry
An example from the real world is flavour symmetry, an SU(3) group corresponding to varying quark flavour. This is an approximate symmetry, violated by quark mass differences and electroweak interactions. Indeed, we see experimentally that particles can be neatly divided into groups that form irreducible representations of the Lie algebra SU(3), as first noted by Murray Gell-MannMurray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
and independently by Yuval Ne'eman
Yuval Ne'eman
Yuval Ne'eman , was a renowned Israeli theoretical physicist, military scientist, and politician. He was a minister in the Israeli government in the 1980s and early 1990s.-Biography:...
(see the eightfold way
Eightfold way (physics)
In physics, the Eightfold Way is a term coined by American physicist Murray Gell-Mann for a theory organizing subatomic baryons and mesons into octets...
).
See also
- Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
- Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
- Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
- Representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
:- Of Lie algebras
- Of Lie groups
- Of the Poincaré groupRepresentation theory of the Poincaré groupIn mathematics, the representation theory of the Poincaré group is an example of the representation theory of a Lie group that is neither a compact group nor a semisimple group. It is fundamental in theoretical physics....
- Special unitary groupSpecial unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
- SymmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
External links
- John C. Baez & John Huerta, The Algebra of Grand Unified Theories,

