
Algebraic bracket
Encyclopedia
In mathematics
, the algebraic bracket or Nijenhuis–Richardson bracket is a graded Lie algebra
structure on the space of alternating multilinear forms of a vector space
to itself, introduced by A. Nijenhuis and R. W. Richardson, Jr (1966, 1967). It is related to but not the same as the Frölicher–Nijenhuis bracket and the Schouten–Nijenhuis bracket.
structures on a vector space, and subsequently the deformations
of these structures. If V is a vector space and p ≥ -1 is an integer, let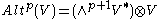
be the space of all skew-symmetric (p+1)-multilinear mappings of V to itself. The direct sum Alt(V) is a graded vector space
. A Lie algebra structure on V is determined by a skew-symmetric bilinear map μ : V × V → V. That is to say, μ is an element of Alt1(V). Furthermore, μ must obey the Jacobi identity
. The Nijenhuis–Richardson bracket supplies a systematic manner for expressing this identity in the form [μ,μ]=0.
In detail, the bracket is a bilinear bracket operation defined on Alt(V) as follows. On homogeneous elements P ∈ Altp(V) and Q ∈ Altq(V), the Nijenhuis–Richardson bracket [P,Q]∧ ∈ Altp+q(V) is given by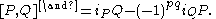
Here the interior product iP is defined by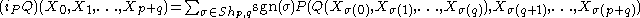
where the sum is over all (p,q) shuffles of the indices. On non-homogeneous elements, the bracket is extended by bilinearity.
in a similar way. Vector valued forms act as derivations on the supercommutative ring Ω*(M) of forms on M
by taking K to the derivation iK, and the Nijenhuis–Richardson bracket then corresponds to the commutator of two derivations. This identifies Ω*(M, T(M)) with the algebra of derivations that vanish on smooth functions. Not all derivations are of this form; for the structure of the full ring of all derivations see the article Frölicher–Nijenhuis bracket.
The Nijenhuis–Richardson bracket and the Frölicher–Nijenhuis bracket both make Ω*(M, T(M)) into a graded superalgebra, but have different degrees.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the algebraic bracket or Nijenhuis–Richardson bracket is a graded Lie algebra
Graded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
structure on the space of alternating multilinear forms of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
to itself, introduced by A. Nijenhuis and R. W. Richardson, Jr (1966, 1967). It is related to but not the same as the Frölicher–Nijenhuis bracket and the Schouten–Nijenhuis bracket.
Definition
The primary motivation for introducing the bracket was to develop a uniform framework for discussing all possible Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
structures on a vector space, and subsequently the deformations
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of these structures. If V is a vector space and p ≥ -1 is an integer, let
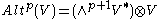
be the space of all skew-symmetric (p+1)-multilinear mappings of V to itself. The direct sum Alt(V) is a graded vector space
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
. A Lie algebra structure on V is determined by a skew-symmetric bilinear map μ : V × V → V. That is to say, μ is an element of Alt1(V). Furthermore, μ must obey the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. The Nijenhuis–Richardson bracket supplies a systematic manner for expressing this identity in the form [μ,μ]=0.
In detail, the bracket is a bilinear bracket operation defined on Alt(V) as follows. On homogeneous elements P ∈ Altp(V) and Q ∈ Altq(V), the Nijenhuis–Richardson bracket [P,Q]∧ ∈ Altp+q(V) is given by
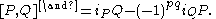
Here the interior product iP is defined by
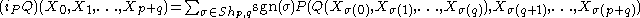
where the sum is over all (p,q) shuffles of the indices. On non-homogeneous elements, the bracket is extended by bilinearity.
Derivations of the ring of forms
The Nijenhuis–Richardson bracket can be defined on the vector valued forms Ω*(M, T(M)) on a smooth manifold Min a similar way. Vector valued forms act as derivations on the supercommutative ring Ω*(M) of forms on M
by taking K to the derivation iK, and the Nijenhuis–Richardson bracket then corresponds to the commutator of two derivations. This identifies Ω*(M, T(M)) with the algebra of derivations that vanish on smooth functions. Not all derivations are of this form; for the structure of the full ring of all derivations see the article Frölicher–Nijenhuis bracket.
The Nijenhuis–Richardson bracket and the Frölicher–Nijenhuis bracket both make Ω*(M, T(M)) into a graded superalgebra, but have different degrees.

