Affiliated operator
Encyclopedia
In mathematics
, affiliated operators were introduced by Murray and von Neumann
in the theory of von Neumann algebras as a technique for using unbounded operator
s to study modules generated by a single vector. Later Atiyah and Singer
showed that index theorems for elliptic operator
s on closed manifold
s with infinite fundamental group
could naturally be phrased in terms of unbounded operators affiliated with the von Neumann algebra of the group. Algebraic properties of affiliated operators have proved important in L2 cohomology, an area between analysis
and geometry
that evolved from the study of such index theorems.
acting on a Hilbert space
H. A closed and densely defined operator A is said to be affiliated with M if A commutes with every unitary operator
U in the commutant of M. Equivalent conditions
are that:
The last condition follows by uniqueness of the polar decomposition. If A has a polar decomposition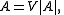
it says that the partial isometry
V should lie in M and that the positive self-adjoint
operator |A| should be affiliated with M. However, by the spectral theorem
, a positive self-adjoint operator commutes with a unitary operator if and only if each of its spectral projections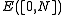
does. This gives another equivalent condition:
and the standard Gelfand–Naimark–Segal action of M on H = L2(M, 
), Edward Nelson
proved that the measurable affiliated operators do form a *-algebra with nice properties: these are operators such that
(I − E([0,N])) < ∞
for N sufficiently large. This algebra of unbounded operators is complete for a natural topology, generalising the notion of convergence in measure
.
It contains all the non-commutative Lp spaces defined by the trace and was introduced to facilitate their study.
This theory can be applied when the von Neumann algebra M is type I or type II. When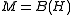
acting on the Hilbert space L2(H) of Hilbert–Schmidt operators, it gives the well-known theory of non-commutative Lp spaces Lp (H) due to Schatten and von Neumann.
When M is in addition a finite von Neumann algebra, for example a type II1 factor, then every affiliated operator is automatically measurable, so the affiliated operators form a *-algebra, as originally observed in the first paper of Murray and von Neumann. In this case M is a von Neumann regular ring
: for on the closure of its image |A| has a measurable inverse B and then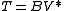
defines a measurable operator with 
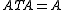. Of course in the classical case when X is a probability space and M = L ∞ (X), we simply recover the *-algebra of measurable functions on X.
If however M is type III, the theory takes a quite different form. Indeed in this case, thanks to the Tomita–Takesaki theory, it is known that the non-commutative Lp spaces are no longer realised by operators affiliated with the von Neumann algebra. As Connes
showed, these spaces can be realised as unbounded operators only by using a certain positive power of the reference modular operator. Instead of being characterised by the simple affiliation relation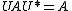
, there is a more complicated bimodule relation involving the analytic continuation of the modular automorphism group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, affiliated operators were introduced by Murray and von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in the theory of von Neumann algebras as a technique for using unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
s to study modules generated by a single vector. Later Atiyah and Singer
Isadore Singer
Isadore Manuel Singer is an Institute Professor in the Department of Mathematics at the Massachusetts Institute of Technology...
showed that index theorems for elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s on closed manifold
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
s with infinite fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
could naturally be phrased in terms of unbounded operators affiliated with the von Neumann algebra of the group. Algebraic properties of affiliated operators have proved important in L2 cohomology, an area between analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
that evolved from the study of such index theorems.
Definition
Let M be a von Neumann algebraVon Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H. A closed and densely defined operator A is said to be affiliated with M if A commutes with every unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
U in the commutant of M. Equivalent conditions
are that:
- each unitary U in M should leave invariant the graph of A defined by
.
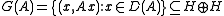- the projection onto G(A) should lie in M2(M).
- each unitary U in M should carry D(A), the domain of A, onto itself and satisfy UAU* = A there.
- each unitary U in M should commute with both operators in the polar decomposition of A.
The last condition follows by uniqueness of the polar decomposition. If A has a polar decomposition
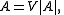
it says that the partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
V should lie in M and that the positive self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
operator |A| should be affiliated with M. However, by the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, a positive self-adjoint operator commutes with a unitary operator if and only if each of its spectral projections
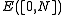
does. This gives another equivalent condition:
- each spectral projection of |A| and the partial isometry in the polar decomposition of A should lie in M.
Measurable operators
In general the operators affiliated with a von Neumann algebra M need not necessarily be well-behaved under either addition or composition. However in the presence of a faithful semi-finite normal trace and the standard Gelfand–Naimark–Segal action of M on H = L2(M, ), Edward NelsonEdward Nelson
Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
proved that the measurable affiliated operators do form a *-algebra with nice properties: these are operators such that
(I − E([0,N])) < ∞for N sufficiently large. This algebra of unbounded operators is complete for a natural topology, generalising the notion of convergence in measure
Convergence in measure
Convergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
.
It contains all the non-commutative Lp spaces defined by the trace and was introduced to facilitate their study.
This theory can be applied when the von Neumann algebra M is type I or type II. When
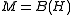acting on the Hilbert space L2(H) of Hilbert–Schmidt operators, it gives the well-known theory of non-commutative Lp spaces Lp (H) due to Schatten and von Neumann.When M is in addition a finite von Neumann algebra, for example a type II1 factor, then every affiliated operator is automatically measurable, so the affiliated operators form a *-algebra, as originally observed in the first paper of Murray and von Neumann. In this case M is a von Neumann regular ring
Von Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
: for on the closure of its image |A| has a measurable inverse B and then
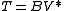defines a measurable operator with 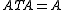. Of course in the classical case when X is a probability space and M = L ∞ (X), we simply recover the *-algebra of measurable functions on X.If however M is type III, the theory takes a quite different form. Indeed in this case, thanks to the Tomita–Takesaki theory, it is known that the non-commutative Lp spaces are no longer realised by operators affiliated with the von Neumann algebra. As Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
showed, these spaces can be realised as unbounded operators only by using a certain positive power of the reference modular operator. Instead of being characterised by the simple affiliation relation
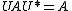, there is a more complicated bimodule relation involving the analytic continuation of the modular automorphism group.