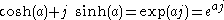Polar decomposition
Encyclopedia
In mathematics
, particularly in linear algebra
and functional analysis
, the polar decomposition of a matrix
or linear operator is a factorization
analogous to the polar form of a nonzero complex number
z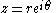
where r is the absolute value
of z (a positive real number
), and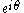 is called the complex sign of z.
is called the complex sign of z.
s H depends on the sphere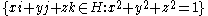 of square roots of minus one. Given any r on this sphere, and an angle –π < a ≤ π, the versor
of square roots of minus one. Given any r on this sphere, and an angle –π < a ≤ π, the versor 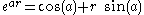 is on the 3-sphere
is on the 3-sphere
of H.
For a = 0 and a = π , the versor is 1 or −1 regardless of which r is selected.
The norm
t of a quaternion q is the Euclidean distance
from the origin to q.
When a quaternion is not just a real number, then there is a unique polar decomposition
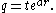
of the form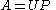
where U is a unitary matrix and P is a positive-semidefinite Hermitian matrix. Intuitively, the polar decomposition separates A into a component that stretches the space along a set of orthogonal axes, represented by P, and a rotation represented by U. The decomposition of the complex conjugate
of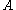 is given by
is given by 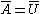
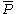 .
.
This decomposition always exists; and so long as A is invertible, it is unique, with P positive-definite
. Note that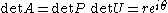
gives the corresponding polar decomposition of the determinant
of A, since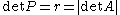 and
and 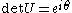 .
.
The matrix P is always unique, even if A is singular, and given by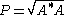
where A* denotes the conjugate transpose
of A. This expression is meaningful since a positive-semidefinite Hermitian matrix has a unique positive-semidefinite square root
. If A is invertible, then the matrix U is given by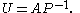
In terms of the singular value decomposition
of A, A = W Σ V*, one has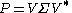
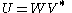
confirming that P is positive-definite and U is unitary.
One can also decompose A in the form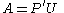
Here U is the same as before and P′ is given by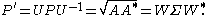
This is known as the left polar decomposition, whereas the previous decomposition is known as the right polar decomposition. Left polar decomposition is also known as reverse polar decomposition.
The matrix A is normal
if and only if P′ = P. Then UΣ = ΣU, and it is possible to diagonalise U with a unitary similarity matrix S that commutes with Σ, giving S U S* = Φ−1, where Φ is a diagonal unitary matrix of phases eiφ. Putting Q = V S*, one can then re-write the polar decomposition as
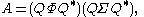
so A then thus also has a spectral decomposition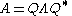
with complex eigenvalues such that ΛΛ* = Σ2 and a unitary matrix of complex eigenvectors Q.
The map from the general linear group
GL(n,C) to the unitary group
U(n) defined by mapping A onto its unitary piece U gives rise to a homotopy equivalence since the space of positive-definite matrices is contractible
. In fact U(n) is a maximal compact subgroup
of GL(n,C).
s is a canonical factorization as the product of a partial isometry
and a non-negative operator.
The polar decomposition for matrices generalizes as follows: if A is a bounded linear operator then there is a unique factorization of A as a product A = UP where U is a partial isometry, P is a non-negative self-adjoint operator and the initial space of U is the closure of the range of P.
The operator U must be weakened to a partial isometry, rather than unitary, because of the following issues. If A is the one-sided shift
on l2(N), then |A| = {A*A}½ = I. So if A = U |A|, U must be A, which is not unitary.
The existence of a polar decomposition is a consequence of Douglas' lemma
:
The operator C can be defined by C(Bh) = Ah, extended by continuity to the closure of Ran(B), and by zero on the orthogonal complement to all of H. The lemma then follows since A*A ≤ B*B implies Ker(A) ⊂ Ker(B).
In particular. If A*A = B*B, then C is a partial isometry, which is unique if Ker(B*) ⊂ Ker(C).
In general, for any bounded operator A,
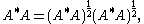
where (A*A)½ is the unique positive square root of A*A given by the usual functional calculus
. So by the lemma, we have
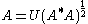
for some partial isometry U, which is unique if Ker(A*) ⊂ Ker(U). Take P to be (A*A)½ and one obtains the polar decomposition A = UP. Notice that an analogous argument can be used to show A = P'U' , where P' is positive and U' a partial isometry.
When H is finite dimensional, U can be extended to a unitary operator; this is not true in general (see example above). Alternatively, the polar decomposition can be shown using the operator version of singular value decomposition.
By property of the continuous functional calculus
, |A| is in the C*-algebra generated by A. A similar but weaker statement holds for the partial isometry: U is in the von Neumann algebra
generated by A. If A is invertible, the polar part U will be in the C*-algebra as well.
between complex Hilbert spaces then it still has a (unique) polar decomposition
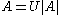
where |A| is a (possibly unbounded) non-negative self adjoint operator with the same domain as A, and U is a partial isometry vanishing on the orthogonal complement of the range Ran(|A|).
The proof uses the same lemma as above, which goes through for unbounded operators in general. If Dom(A*A) =
Dom(B*B) and A*Ah = B*Bh for all h ∈ Dom(A*A), then there exists a partial isometry U such that A = UB. U is unique if Ran(B)⊥⊂ Ker(U). The operator A being closed and densely defined ensures that the operator A*A is self-adjoint (with dense domain) and therefore allows one to define (A*A)½. Applying the lemma gives polar decomposition.
If an unbounded operator A is affiliated
to a von Neumann algebra M, and A = UP is its polar decomposition, then U is in M and so is the spectral projection of P, 1B(P), for any Borel set B in [0, ∞).
decompositions arise as follows:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the polar decomposition of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
or linear operator is a factorization
Matrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
analogous to the polar form of a nonzero complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
z
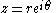
where r is the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of z (a positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
), and
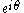 is called the complex sign of z.
is called the complex sign of z.Quaternion polar decomposition
The polar decomposition of quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s H depends on the sphere
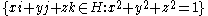 of square roots of minus one. Given any r on this sphere, and an angle –π < a ≤ π, the versor
of square roots of minus one. Given any r on this sphere, and an angle –π < a ≤ π, the versor 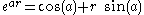 is on the 3-sphere
is on the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
of H.
For a = 0 and a = π , the versor is 1 or −1 regardless of which r is selected.
The norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
t of a quaternion q is the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
from the origin to q.
When a quaternion is not just a real number, then there is a unique polar decomposition
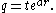
Matrix polar decomposition
The polar decomposition of a square complex matrix A is a matrix decompositionMatrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
of the form
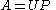
where U is a unitary matrix and P is a positive-semidefinite Hermitian matrix. Intuitively, the polar decomposition separates A into a component that stretches the space along a set of orthogonal axes, represented by P, and a rotation represented by U. The decomposition of the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of
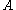 is given by
is given by 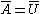
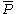 .
.This decomposition always exists; and so long as A is invertible, it is unique, with P positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
. Note that
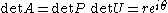
gives the corresponding polar decomposition of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A, since
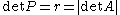 and
and 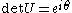 .
.The matrix P is always unique, even if A is singular, and given by
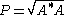
where A* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A. This expression is meaningful since a positive-semidefinite Hermitian matrix has a unique positive-semidefinite square root
Square root of a matrix
In mathematics, the square root of a matrix extends the notion of square root from numbers to matrices. A matrix B is said to be a square root of A if the matrix product B · B is equal to A.-Properties:...
. If A is invertible, then the matrix U is given by
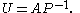
In terms of the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of A, A = W Σ V*, one has
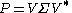
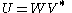
confirming that P is positive-definite and U is unitary.
One can also decompose A in the form
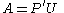
Here U is the same as before and P′ is given by
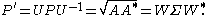
This is known as the left polar decomposition, whereas the previous decomposition is known as the right polar decomposition. Left polar decomposition is also known as reverse polar decomposition.
The matrix A is normal
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
if and only if P′ = P. Then UΣ = ΣU, and it is possible to diagonalise U with a unitary similarity matrix S that commutes with Σ, giving S U S* = Φ−1, where Φ is a diagonal unitary matrix of phases eiφ. Putting Q = V S*, one can then re-write the polar decomposition as
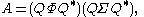
so A then thus also has a spectral decomposition
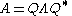
with complex eigenvalues such that ΛΛ* = Σ2 and a unitary matrix of complex eigenvectors Q.
The map from the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n,C) to the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) defined by mapping A onto its unitary piece U gives rise to a homotopy equivalence since the space of positive-definite matrices is contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
. In fact U(n) is a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of GL(n,C).
Bounded operators on Hilbert space
The polar decomposition of any bounded linear operator A between complex Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s is a canonical factorization as the product of a partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
and a non-negative operator.
The polar decomposition for matrices generalizes as follows: if A is a bounded linear operator then there is a unique factorization of A as a product A = UP where U is a partial isometry, P is a non-negative self-adjoint operator and the initial space of U is the closure of the range of P.
The operator U must be weakened to a partial isometry, rather than unitary, because of the following issues. If A is the one-sided shift
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
on l2(N), then |A| = {A*A}½ = I. So if A = U |A|, U must be A, which is not unitary.
The existence of a polar decomposition is a consequence of Douglas' lemma
Douglas' lemma
In operator theory, an area of mathematics, Douglas' lemma relates factorization, range inclusion, and majorization of Hilbert space operators. It is generally attributed to Ronald G. Douglas, although Douglas acknowledges that aspects of the result may already have been known...
:
- Lemma If A, B are bounded operators on a Hilbert space H, and A*A ≤ B*B, then there exists a contraction C such that A = CB. Furthermore, C is unique if Ker(B*) ⊂ Ker(C).
The operator C can be defined by C(Bh) = Ah, extended by continuity to the closure of Ran(B), and by zero on the orthogonal complement to all of H. The lemma then follows since A*A ≤ B*B implies Ker(A) ⊂ Ker(B).
In particular. If A*A = B*B, then C is a partial isometry, which is unique if Ker(B*) ⊂ Ker(C).
In general, for any bounded operator A,
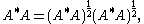
where (A*A)½ is the unique positive square root of A*A given by the usual functional calculus
Functional calculus
In mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
. So by the lemma, we have
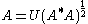
for some partial isometry U, which is unique if Ker(A*) ⊂ Ker(U). Take P to be (A*A)½ and one obtains the polar decomposition A = UP. Notice that an analogous argument can be used to show A = P'U' , where P' is positive and U' a partial isometry.
When H is finite dimensional, U can be extended to a unitary operator; this is not true in general (see example above). Alternatively, the polar decomposition can be shown using the operator version of singular value decomposition.
By property of the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
, |A| is in the C*-algebra generated by A. A similar but weaker statement holds for the partial isometry: U is in the von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
generated by A. If A is invertible, the polar part U will be in the C*-algebra as well.
Unbounded operators
If A is a closed, densely defined unbounded operatorUnbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
between complex Hilbert spaces then it still has a (unique) polar decomposition
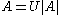
where |A| is a (possibly unbounded) non-negative self adjoint operator with the same domain as A, and U is a partial isometry vanishing on the orthogonal complement of the range Ran(|A|).
The proof uses the same lemma as above, which goes through for unbounded operators in general. If Dom(A*A) =
Dom(B*B) and A*Ah = B*Bh for all h ∈ Dom(A*A), then there exists a partial isometry U such that A = UB. U is unique if Ran(B)⊥⊂ Ker(U). The operator A being closed and densely defined ensures that the operator A*A is self-adjoint (with dense domain) and therefore allows one to define (A*A)½. Applying the lemma gives polar decomposition.
If an unbounded operator A is affiliated
Affiliated operator
In mathematics, affiliated operators were introduced by Murray and von Neumann in the theory of von Neumann algebras as a technique for using unbounded operators to study modules generated by a single vector...
to a von Neumann algebra M, and A = UP is its polar decomposition, then U is in M and so is the spectral projection of P, 1B(P), for any Borel set B in [0, ∞).
Alternative planar decompositions
In the Cartesian plane, alternative planar ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
decompositions arise as follows:
- If x ≠ 0, z = x ( 1 + (y/x) ε) is a polar decomposition of a dual numberDual numberIn linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
z = x + y ε, where ε ε = 0. In this polar decomposition, the unit circle has been replaced by the line x = 1, the polar angle by the slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
y/x, and the radius x is negative in the left half-plane.
- If x2 ≠ y2, then the unit hyperbolaUnit hyperbolaIn geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
x2 − y2 = 1 and its conjugate x2 − y2 = −1 can be used to form a polar decomposition based on the branch of the unit hyperbola through (1,0). This branch is parametrized by the hyperbolic angleHyperbolic angleIn mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
a and is written
-
- where j j = +1 and the arithmetic of split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s is used. The branch through (−1,0) is traced by −ea j. Since the operation of multiplying by j reflects a point across the line y = x, the second hyperbola has branches traced by jea j or −jea j. Therefore a point in one of the quadrants has a polar decomposition in one of the forms: - The set (1,−1,j,−j) has products that make it isomorphic to the Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
. Evidently polar decomposition in this case involves an element from that group.