Z-group
Encyclopedia
In mathematics
, especially in the area of algebra
known as group theory
, the term Z-group refers to a number of distinct types of groups
:
In the study of finite group
s, a Z-group is a finite group whose Sylow subgroups are all cyclic
. The Z originates both from the German Zyklische and from their classification in . In many standard textbooks these groups have no special name, other than metacyclic groups, but that term is often used more generally today. See metacyclic group
for more on the general, modern definition which includes non-cyclic p-groups
; see for the stricter, classical definition more closely related to Z-groups.
Every group whose Sylow subgroups are cyclic is itself metacyclic
, so supersolvable
. In fact, such a group has a cyclic derived subgroup with cyclic maximal abelian quotient. Such a group has the presentation :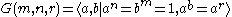
, where mn is the order of G(m,n,r), the greatest common divisor
, gcd((r-1)n, m) = 1, and rn ≡ 1 (mod m).
The character theory
of Z-groups is well understood , as they are monomial group
s.
The derived length of a Z-group is at most 2, so Z-groups may be insufficient for some uses. A generalization due to Hall are the A-group
s, those groups with abelian
Sylow subgroups. These groups behave similarly to Z-groups, but can have arbitrarily large derived length . Another generalization due to allows the Sylow 2-subgroup more flexibility, including dihedral
and generalized quaternion groups.
The definition of central series
used for Z-group is somewhat technical. A series of G is a collection S of subgroups of G, linearly ordered by inclusion, such that for every g in G, the subgroups Ag = ∩ { N in S : g in N } and Bg = ∪ { N in S : g not in N } are both in S. A (generalized) central series of G is a series such that every N in S is normal in G and such that for every g in G, the quotient Ag/Bg is contained in the center of G/Bg. A Z-group is a group with such a (generalized) central series. Examples include the hypercentral groups whose transfinite upper central series form such a central series, as well as the hypocentral groups whose transfinite lower central series form such a central series .
A (Z)-group is a group faithfully represented as a doubly transitive permutation group in which no non-identity element fixes more than two points. A (ZT)-group is a (Z)-group that is of odd degree and not a Frobenius group
, that is a Zassenhaus group
of odd degree, also known as one of the groups PSL(2,2k+1) or Sz(22k+1), for k any positive integer .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the term Z-group refers to a number of distinct types of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
:
- in the study of finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, a Z-group is a finite groups whose Sylow subgroups are all cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. - in the study of infinite groupInfinite groupIn group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....
s, a Z-group is a group which possesses a very general form of central seriesCentral seriesIn mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
. - occasionally, (Z)-group is used to mean a Zassenhaus groupZassenhaus groupIn mathematics, a Zassenhaus group, named after Hans Julius Zassenhaus, is a certain sort of doubly transitive permutation group very closely related to rank-1 groups of Lie type.- Definition :...
, a special type of permutation groupPermutation groupIn mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
.
Groups whose Sylow subgroups are cyclic
- Usage: , , , ,
In the study of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, a Z-group is a finite group whose Sylow subgroups are all cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. The Z originates both from the German Zyklische and from their classification in . In many standard textbooks these groups have no special name, other than metacyclic groups, but that term is often used more generally today. See metacyclic group
Metacyclic group
In group theory, a metacyclic group is an extension of a cyclic group by a cyclic group. That is, it is a group G for which there is a short exact sequence1 \rightarrow K \rightarrow G \rightarrow H \rightarrow 1,\,where H and K are cyclic...
for more on the general, modern definition which includes non-cyclic p-groups
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
; see for the stricter, classical definition more closely related to Z-groups.
Every group whose Sylow subgroups are cyclic is itself metacyclic
Metacyclic group
In group theory, a metacyclic group is an extension of a cyclic group by a cyclic group. That is, it is a group G for which there is a short exact sequence1 \rightarrow K \rightarrow G \rightarrow H \rightarrow 1,\,where H and K are cyclic...
, so supersolvable
Supersolvable group
In mathematics, a group is supersolvable if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.-Definition:Let G be a group...
. In fact, such a group has a cyclic derived subgroup with cyclic maximal abelian quotient. Such a group has the presentation :
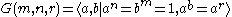, where mn is the order of G(m,n,r), the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
, gcd((r-1)n, m) = 1, and rn ≡ 1 (mod m).
The character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of Z-groups is well understood , as they are monomial group
Monomial group
In mathematics, in the area of algebra studying the character theory of finite groups, an M-group or monomial group is a finite group whose complex irreducible characters are all monomial, that is, induced from characters of degree 1 ....
s.
The derived length of a Z-group is at most 2, so Z-groups may be insufficient for some uses. A generalization due to Hall are the A-group
A-group
A-Group is the designation for a distinct culture that arose between the First and Second Cataracts of the Nile in Nubia betweenthe Egyptian 1st dynasty and the 3rd millennium BC.The A-Group settled on very poor land with scarce natural resources, yet...
s, those groups with abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Sylow subgroups. These groups behave similarly to Z-groups, but can have arbitrarily large derived length . Another generalization due to allows the Sylow 2-subgroup more flexibility, including dihedral
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
and generalized quaternion groups.
Group with a generalized central series
- Usage: ,
The definition of central series
Central series
In mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
used for Z-group is somewhat technical. A series of G is a collection S of subgroups of G, linearly ordered by inclusion, such that for every g in G, the subgroups Ag = ∩ { N in S : g in N } and Bg = ∪ { N in S : g not in N } are both in S. A (generalized) central series of G is a series such that every N in S is normal in G and such that for every g in G, the quotient Ag/Bg is contained in the center of G/Bg. A Z-group is a group with such a (generalized) central series. Examples include the hypercentral groups whose transfinite upper central series form such a central series, as well as the hypocentral groups whose transfinite lower central series form such a central series .
Special 2-transitive groups
- Usage:
A (Z)-group is a group faithfully represented as a doubly transitive permutation group in which no non-identity element fixes more than two points. A (ZT)-group is a (Z)-group that is of odd degree and not a Frobenius group
Frobenius group
In mathematics, a Frobenius group is a transitive permutation group on a finite set, such that no non-trivial elementfixes more than one point and some non-trivial element fixes a point.They are named after F. G. Frobenius.- Structure :...
, that is a Zassenhaus group
Zassenhaus group
In mathematics, a Zassenhaus group, named after Hans Julius Zassenhaus, is a certain sort of doubly transitive permutation group very closely related to rank-1 groups of Lie type.- Definition :...
of odd degree, also known as one of the groups PSL(2,2k+1) or Sz(22k+1), for k any positive integer .