Vietoris–Begle mapping theorem
Encyclopedia
The Vietoris–Begle mapping theorem is a result in the mathematical
field of algebraic topology
. It is named for Leopold Vietoris
and Edward G. Begle
. The statement of the theorem, below, is as formulated by Stephen Smale
.
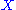and 
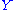be compact
metric spaces, and let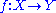
be surjective
and continuous
. Suppose that the fibers
of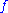
are acyclic
, so that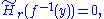
for all 
and all 
,
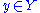with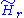
denoting the 
th reduced homology
group
. Then, the induced homomorphism
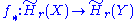
is an isomorphism
for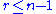
and a surjection for 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. It is named for Leopold Vietoris
Leopold Vietoris
Leopold Vietoris was an Austrian mathematician and a World War I veteran who gained additional fame by becoming a supercentenarian...
and Edward G. Begle
Edward G. Begle
Edward Griffith Begle was a mathematician best known for his role as the director of the School Mathematics Study Group , the primary group credited for developing what came to be known as The New Math...
. The statement of the theorem, below, is as formulated by Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
.
Theorem
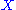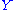Let and be compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
metric spaces, and let
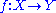be surjectiveSurjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
and continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Suppose that the fibers
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of
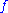are acyclicAcyclic
Acyclic can refer to:* In chemistry, a compound which is not cyclic, e.g. alkanes and acyclic aliphatic compounds* In mathematics:** A graph without a cycle, especially*** A directed acyclic graph...
, so that
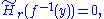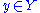for all and all ,with
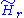denoting the th reduced homologyReduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Then, the induced homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
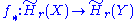
is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
for
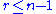and a surjection for .