
Theta-divisor
Encyclopedia
In mathematics
, the theta divisor Θ is the divisor
in the sense of algebraic geometry
defined on an abelian variety
A over the complex numbers (and principally polarized) by the zero locus of the associated Riemann theta-function. It is therefore an algebraic subvariety of A of dimension dim A − 1.
describe Θ in another way, in the case that A is the Jacobian variety
J of an algebraic curve
(compact Riemann surface
) C. There is, for a choice of base point P on C, a standard mapping of C to J, by means of the interpretation of J as the linear equivalence classes of divisors on C of degree 0. That is, Q on C maps to the class of Q − P. Then since J is an algebraic group
, C may be added to itself k times on J, giving rise to subvarieties Wk.
If g is the genus
of C, Riemann proved that Θ is a translate on J of Wg − 1. He also described which points on Wg − 1 are non-singular: they correspond to the effective divisors D of degree g − 1 with no associated meromorphic functions other than constants. In more classical language, these D do not move in a linear system of divisors
on C, in the sense that they do not dominate the polar divisor of a non constant function.
Riemann further proved the Riemann singularity theorem, identifying the multiplicity of a point p = class(D) on Wg − 1 as the number of independent meromorphic functions with pole divisor dominated by D, or equivalently as h0(O(D)) , the number of independent global sections of the holomorphic line bundle associated to D as Cartier divisor on C.
and Andreotti - Mayer, to a description of the singularities of points p = class(D) on Wk for 1 ≤ k ≤ g − 1. In particular he computed their multiplicities also in terms of the number of independent meromorphic functions associated to D (Riemann-Kempf singularity theorem).
More precisely, Kempf mapped J locally near p to a family of matrices coming from an exact sequence
which computes h0(O(D)), in such a way that Wk corresponds to the locus of matrices of less than maximal rank. The multiplicity then agrees with that of the point on the corresponding rank locus. Explicitly, if
the multiplicity of Wk at class(D) is the binomial coefficient
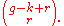
When d = g − 1, this is r + 1, Riemann's formula.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the theta divisor Θ is the divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
in the sense of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
defined on an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
A over the complex numbers (and principally polarized) by the zero locus of the associated Riemann theta-function. It is therefore an algebraic subvariety of A of dimension dim A − 1.
Classical theory
Classical results of Bernhard RiemannBernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
describe Θ in another way, in the case that A is the Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
J of an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
(compact Riemann surface
Compact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
) C. There is, for a choice of base point P on C, a standard mapping of C to J, by means of the interpretation of J as the linear equivalence classes of divisors on C of degree 0. That is, Q on C maps to the class of Q − P. Then since J is an algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, C may be added to itself k times on J, giving rise to subvarieties Wk.
If g is the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of C, Riemann proved that Θ is a translate on J of Wg − 1. He also described which points on Wg − 1 are non-singular: they correspond to the effective divisors D of degree g − 1 with no associated meromorphic functions other than constants. In more classical language, these D do not move in a linear system of divisors
Linear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
on C, in the sense that they do not dominate the polar divisor of a non constant function.
Riemann further proved the Riemann singularity theorem, identifying the multiplicity of a point p = class(D) on Wg − 1 as the number of independent meromorphic functions with pole divisor dominated by D, or equivalently as h0(O(D)) , the number of independent global sections of the holomorphic line bundle associated to D as Cartier divisor on C.
Later work
The Riemann singularity theorem was extended by George Kempf in 1973, building on work of David MumfordDavid Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
and Andreotti - Mayer, to a description of the singularities of points p = class(D) on Wk for 1 ≤ k ≤ g − 1. In particular he computed their multiplicities also in terms of the number of independent meromorphic functions associated to D (Riemann-Kempf singularity theorem).
More precisely, Kempf mapped J locally near p to a family of matrices coming from an exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
which computes h0(O(D)), in such a way that Wk corresponds to the locus of matrices of less than maximal rank. The multiplicity then agrees with that of the point on the corresponding rank locus. Explicitly, if
- h0(O(D)) = r + 1,
the multiplicity of Wk at class(D) is the binomial coefficient
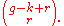
When d = g − 1, this is r + 1, Riemann's formula.

