Symmetry operation
Encyclopedia
In the context of molecular symmetry
, a symmetry operation may be defined as a permutation
of atoms such that the molecule
or crystal
is transformed into a state indistinguishable from the starting state.
Two basic facts follow from this definition, which emphasize its usefulness.
C1, rotation by 360°, is called the Identity operation and is denoted by E or I.
Cnn , n rotations 360°/n is also an Identity operation.
S1 is usually denoted as σ, a reflection operation about a mirror plane.
S2 is usually denoted as i, an inversion operation about an inversion centre.
When n is an even number Snn = E, but when n is odd Sn2n = E.
Rotation axes, mirror planes and inversion centres are symmetry elements
, not operations. The rotation axis of highest order is known as the principal rotation axis. It is conventional to set the Cartesian z axis of the molecule to contain the principal rotation axis.
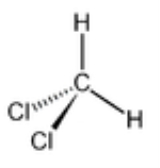
 Dichloromethane, CH2Cl2. There is a C2 rotation axis which passes through the carbon atom and the mid points between the two hydrogen atoms and the two chlorine atoms. Define the z axis as co-linear
Dichloromethane, CH2Cl2. There is a C2 rotation axis which passes through the carbon atom and the mid points between the two hydrogen atoms and the two chlorine atoms. Define the z axis as co-linear
with the C2 axis, the xz plane as containing CH2 and the yz plane as containing CCl2. A C2 rotation operation permutes the two hydrogen atoms and the two chlorine atoms. Reflection in the yz plane permutes the hydrogen atoms while reflection in the xz plane permutes the chlorine atoms. The four symmetry operations E, C2, σ(xz)and σ(yz) form the point group
C2v. Note that if any two operations are carried out in succession the result is the same as if a single operation of the group had been performed.
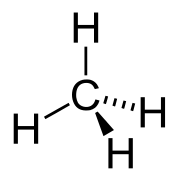 Methane, CH4. In addition to the proper rotations of order 2 and 3 there are three mutually perpendicular S4 axes which pass half-way between the C-H bonds and six mirror planes. Note that S42 = C2.
Methane, CH4. In addition to the proper rotations of order 2 and 3 there are three mutually perpendicular S4 axes which pass half-way between the C-H bonds and six mirror planes. Note that S42 = C2.
Molecular symmetry
Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can predict or explain many of a molecule's chemical properties, such as its dipole moment...
, a symmetry operation may be defined as a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of atoms such that the molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
or crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
is transformed into a state indistinguishable from the starting state.
Two basic facts follow from this definition, which emphasize its usefulness.
- Physical properties and wave functions must be invariantInvariant (physics)In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
with respect to symmetry operations. - Symmetry operations can be collected together in groups which are isomorphousIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to permutation groups.
Proper rotation operations
These are denoted by Cnm and are rotations of 360°/n, performed m times. The superscript m is omitted if it is equal to one.C1, rotation by 360°, is called the Identity operation and is denoted by E or I.
Cnn , n rotations 360°/n is also an Identity operation.
Improper rotation operations
These are denoted by Snm and are rotations of 360°/n followed by reflection in a plane perpendicular to the rotation axis.S1 is usually denoted as σ, a reflection operation about a mirror plane.
S2 is usually denoted as i, an inversion operation about an inversion centre.
When n is an even number Snn = E, but when n is odd Sn2n = E.
Rotation axes, mirror planes and inversion centres are symmetry elements
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, not operations. The rotation axis of highest order is known as the principal rotation axis. It is conventional to set the Cartesian z axis of the molecule to contain the principal rotation axis.
Examples

Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
with the C2 axis, the xz plane as containing CH2 and the yz plane as containing CCl2. A C2 rotation operation permutes the two hydrogen atoms and the two chlorine atoms. Reflection in the yz plane permutes the hydrogen atoms while reflection in the xz plane permutes the chlorine atoms. The four symmetry operations E, C2, σ(xz)and σ(yz) form the point group
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
C2v. Note that if any two operations are carried out in succession the result is the same as if a single operation of the group had been performed.


