Spectral theory of compact operators
Encyclopedia
In functional analysis
, compact operator
s are linear operators that map bounded sets to precompact set
s. The set of compact operators acting on a Hilbert space H is the closure of the set of finite rank operators in the uniform operator topology. In general, operators on infinite dimensional spaces feature properties that do not appear in the finite dimensional case, i.e. for matrices. The family of compact operators are notable in that they share as much similarity with matrices as one can expect from a general operator. In particular, the spectral properties of compact operators resemble those of square matrices.
This article first summarizes the corresponding results from the matrix case before discussing the spectral properties of compact operators. The reader will see that most statements transfer verbatim from the matrix case.
The spectral theory of compact operators was first developed by F. Riesz.
Theorem Let A be an n × n complex matrix, i.e. A a linear operator acting on Cn. If λ1...λk are the distinct eigenvalues of A, then Cn can be decomposed into the invariant subspaces of A
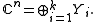
The subspace Yi = Ker(λi - A)m where Ker(λi - A)m = Ker(λi - A)m+1. Furthermore, the poles of the resolvent function ζ → (ζ - A)-1 coincide with the set of eigenvalues of A.
of C. The spectral properties of C are:
Theorem
i) Every nonzero λ ∈ σ(C) is an eigenvalue of C.
ii) For all nonzero λ ∈ σ(C), there exist m such that Ker(λi - A)m = Ker(λi - A)m+1.
iii) The eigenvalues can only accumulate at 0. If the dimension of X is not finite, then σ(C) must contain 0.
iv) σ(C) is countable.
v) Every nonzero λ ∈ σ(C) is a pole of the resolvent function ζ → (ζ - C)-1.
:
Lemma 1 Let X be a Banach space and Y ⊂ X, Y ≠ X, be a closed subspace. For all ε > 0, there exists x ∈ X such that ||x|| = 1 and
where d(x, Y) is the distance from x to Y.
This fact will be used repeatedly in the argument leading to the theorem. Notice that when X is a Hilbert space, the lemma is trivial.
Another useful fact is:
Lemma 2 If C is compact, then Ran(I - C) is closed.
Proof: Let (I - C)xn → y in norm. If {xn} is bounded, then there exist a weakly convergent subsequence xn k. Compactness of C implies C xn k is norm convergent. So xn k = (I - C)xn k + C xn k is norm convergent, to some x. This gives (I - C)xn k → (I - C)x = y. The same argument goes through if the distances d(xn, Ker(I - C)) is bounded.
But d(xn, Ker(I - C)) must be bounded. Suppose this is not the case. Pass now to the quotient map of (I - C), still denoted by (I - C), on X/Ker(I - C). The quotient norm on X/Ker(I - C) is still denoted by ||·||, and {xn} are now viewed as representatives of their equivalence classes in the quotient space. Take a subsequence {xn k} such that ||xn k|| > k and define a sequence of unit vectors by zn k = xn k/||xn k||. Again we would have (I - C)zn k → (I - C)z for some z. Since ||(I - C)zn k|| = ||(I - C)xn k||/ ||xn k|| → 0, we have (I - C)z = 0 i.e. z ∈ Ker(I - C). Since we passed to the quotient map, z = 0. This is impossible because z is the norm limit of a sequence of unit vectors. Thus the lemma is proven.
We are now ready to prove the theorem.
i) Without loss of generality, assume λ = 1. λ ∈ σ(C) not being an eigenvalue means (I - C) is injective but not surjective. By Lemma 2, Y1 = Ran(I - C) is a closed proper subspace of X. Since (I - C) is injective, Y2 = (I - C)Y1 is again a closed proper subspace of Y1. Define Yn = Ran(I - C)n. Consider the decreasing sequence of subspaces
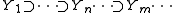
where all inclusions are proper. By lemma 1, we can choose unit vectors yn ∈ Yn such that d(yn, Yn+1) > ½. Compactness of C means {C yn} must contain a norm convergent subsequence. But for n < m
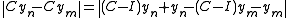
and notice that
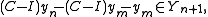
which implies ||Cyn - Cym|| > ½. This is a contradiction, and so λ must be an eigenvalue.
ii) The sequence { Yn = Ker(λi - A)n} is an increasing sequence of closed subspaces. The theorem claims it stops. Suppose it does not stop, i.e. the inclusion Ker(λi - A)n ⊂ Ker(λi - A)n+1 is proper for all n. By lemma 1, there exists a sequence {yn}n ≥ 2 of unit vectors such that yn ∈ Yn and d(yn, Yn - 1) > ½. As before, compactness of C means {C yn} must contain a norm convergent subsequence. But for n < m
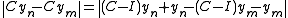
and notice that
which implies ||Cyn - Cym|| > ½. This is a contradiction, and so the sequence { Yn = Ker(λi - A)n} must terminate at some finite m.
iii) Suppose eigenvalues of C do not accumulate at 0. We can therefore assume that there exist a sequence of distinct eigenvalues {λn}, with corresponding eigenvectors {xn}, such that |λn| > ε for all n. Define Yn = span{x1...xn}. The sequence {Yn} is a strictly increasing sequence. Choose unit vectors such that yn ∈ Yn and d(yn, Yn - 1) = 1. Then for n < m
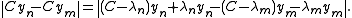
But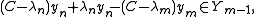
therefore ||Cyn - Cym|| > ε, a contradiction.
iv) This is an immediate consequence of iii). The set of eigenvalues {λ} is the union
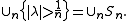
Because σ(C) is a bounded set and the eigenvalues can only accumulate at 0, each Sn is finite, which gives the desired result.
v) As in the matrix case, this is a direct application of the holomorphic functional calculus
.
where γ is a Jordan contour that encloses only λ from σ(C). Let Y be the subspace Y = E(λ)X. C restricted to Y is a compact invertible operator with spectrum {λ}, therefore Y is finite dimensional. Let ν be such that Ker(λ - C)ν = Ker(λ - C)ν + 1. By inspecting the Jordan form, we see that (λ - C)ν = 0 while (λ - C)ν - 1 ≠ 0. The Laurent series of the resolvent mapping centered at λ shows that
So Y = Ker(λ - C)ν.
The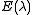
satisfy 
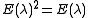, so that they are indeed projection operators or spectral projections. By definition they commute with C.
Moreover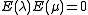
if 
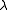and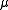 
are distinct.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s are linear operators that map bounded sets to precompact set
Precompact set
Precompact set may refer to:* Relatively compact subspace, a subset whose closure is compact* Totally bounded set, a subset that can be covered by finitely many subsets of fixed size...
s. The set of compact operators acting on a Hilbert space H is the closure of the set of finite rank operators in the uniform operator topology. In general, operators on infinite dimensional spaces feature properties that do not appear in the finite dimensional case, i.e. for matrices. The family of compact operators are notable in that they share as much similarity with matrices as one can expect from a general operator. In particular, the spectral properties of compact operators resemble those of square matrices.
This article first summarizes the corresponding results from the matrix case before discussing the spectral properties of compact operators. The reader will see that most statements transfer verbatim from the matrix case.
The spectral theory of compact operators was first developed by F. Riesz.
Spectral theory of matrices
The classical result for square matrices is the Jordan canonical form, which states the following:Theorem Let A be an n × n complex matrix, i.e. A a linear operator acting on Cn. If λ1...λk are the distinct eigenvalues of A, then Cn can be decomposed into the invariant subspaces of A
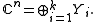
The subspace Yi = Ker(λi - A)m where Ker(λi - A)m = Ker(λi - A)m+1. Furthermore, the poles of the resolvent function ζ → (ζ - A)-1 coincide with the set of eigenvalues of A.
Statement
Let X be a Banach space, C be a compact operator acting on X, and σ(C) be the spectrumSpectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of C. The spectral properties of C are:
Theorem
i) Every nonzero λ ∈ σ(C) is an eigenvalue of C.
ii) For all nonzero λ ∈ σ(C), there exist m such that Ker(λi - A)m = Ker(λi - A)m+1.
iii) The eigenvalues can only accumulate at 0. If the dimension of X is not finite, then σ(C) must contain 0.
iv) σ(C) is countable.
v) Every nonzero λ ∈ σ(C) is a pole of the resolvent function ζ → (ζ - C)-1.
Proof
The theorem claims several properties of the operator λ - C where λ ≠ 0. Without loss of generality, it can be assumed that λ = 1. Therefore we consider I - C, I being the identity operator. The proof will require two lemmas. The first is called Riesz's lemmaRiesz's lemma
Riesz's lemma is a lemma in functional analysis. It specifies conditions which guarantee that a subspace in a normed linear space is dense.- The result :...
:
Lemma 1 Let X be a Banach space and Y ⊂ X, Y ≠ X, be a closed subspace. For all ε > 0, there exists x ∈ X such that ||x|| = 1 and
where d(x, Y) is the distance from x to Y.
This fact will be used repeatedly in the argument leading to the theorem. Notice that when X is a Hilbert space, the lemma is trivial.
Another useful fact is:
Lemma 2 If C is compact, then Ran(I - C) is closed.
Proof: Let (I - C)xn → y in norm. If {xn} is bounded, then there exist a weakly convergent subsequence xn k. Compactness of C implies C xn k is norm convergent. So xn k = (I - C)xn k + C xn k is norm convergent, to some x. This gives (I - C)xn k → (I - C)x = y. The same argument goes through if the distances d(xn, Ker(I - C)) is bounded.
But d(xn, Ker(I - C)) must be bounded. Suppose this is not the case. Pass now to the quotient map of (I - C), still denoted by (I - C), on X/Ker(I - C). The quotient norm on X/Ker(I - C) is still denoted by ||·||, and {xn} are now viewed as representatives of their equivalence classes in the quotient space. Take a subsequence {xn k} such that ||xn k|| > k and define a sequence of unit vectors by zn k = xn k/||xn k||. Again we would have (I - C)zn k → (I - C)z for some z. Since ||(I - C)zn k|| = ||(I - C)xn k||/ ||xn k|| → 0, we have (I - C)z = 0 i.e. z ∈ Ker(I - C). Since we passed to the quotient map, z = 0. This is impossible because z is the norm limit of a sequence of unit vectors. Thus the lemma is proven.
We are now ready to prove the theorem.
i) Without loss of generality, assume λ = 1. λ ∈ σ(C) not being an eigenvalue means (I - C) is injective but not surjective. By Lemma 2, Y1 = Ran(I - C) is a closed proper subspace of X. Since (I - C) is injective, Y2 = (I - C)Y1 is again a closed proper subspace of Y1. Define Yn = Ran(I - C)n. Consider the decreasing sequence of subspaces
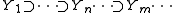
where all inclusions are proper. By lemma 1, we can choose unit vectors yn ∈ Yn such that d(yn, Yn+1) > ½. Compactness of C means {C yn} must contain a norm convergent subsequence. But for n < m
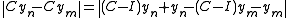
and notice that
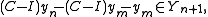
which implies ||Cyn - Cym|| > ½. This is a contradiction, and so λ must be an eigenvalue.
ii) The sequence { Yn = Ker(λi - A)n} is an increasing sequence of closed subspaces. The theorem claims it stops. Suppose it does not stop, i.e. the inclusion Ker(λi - A)n ⊂ Ker(λi - A)n+1 is proper for all n. By lemma 1, there exists a sequence {yn}n ≥ 2 of unit vectors such that yn ∈ Yn and d(yn, Yn - 1) > ½. As before, compactness of C means {C yn} must contain a norm convergent subsequence. But for n < m
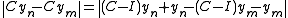
and notice that
which implies ||Cyn - Cym|| > ½. This is a contradiction, and so the sequence { Yn = Ker(λi - A)n} must terminate at some finite m.
iii) Suppose eigenvalues of C do not accumulate at 0. We can therefore assume that there exist a sequence of distinct eigenvalues {λn}, with corresponding eigenvectors {xn}, such that |λn| > ε for all n. Define Yn = span{x1...xn}. The sequence {Yn} is a strictly increasing sequence. Choose unit vectors such that yn ∈ Yn and d(yn, Yn - 1) = 1. Then for n < m
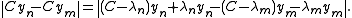
But
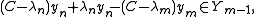
therefore ||Cyn - Cym|| > ε, a contradiction.
iv) This is an immediate consequence of iii). The set of eigenvalues {λ} is the union
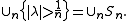
Because σ(C) is a bounded set and the eigenvalues can only accumulate at 0, each Sn is finite, which gives the desired result.
v) As in the matrix case, this is a direct application of the holomorphic functional calculus
Holomorphic functional calculus
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function ƒ of a complex argument z and an operator T, the aim is to construct an operatorf\,...
.
Invariant subspaces
As in the matrix case, the above spectral properties lead to a decomposition of X into invariant subspaces of a compact operator C. Let λ ≠ 0 be an eigenvalue of C; so λ is an isolated point of σ(C). Using the holomorphic functional calculus, define the Riesz projection E(λ) bywhere γ is a Jordan contour that encloses only λ from σ(C). Let Y be the subspace Y = E(λ)X. C restricted to Y is a compact invertible operator with spectrum {λ}, therefore Y is finite dimensional. Let ν be such that Ker(λ - C)ν = Ker(λ - C)ν + 1. By inspecting the Jordan form, we see that (λ - C)ν = 0 while (λ - C)ν - 1 ≠ 0. The Laurent series of the resolvent mapping centered at λ shows that
So Y = Ker(λ - C)ν.
The
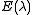satisfy 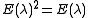, so that they are indeed projection operators or spectral projections. By definition they commute with C.Moreover
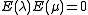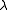if and 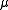are distinct.- Let
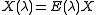if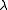 
is a non-zero eigenvalue. Thus 
is a finite-dimensional invariant subspace, the generalised eigenspace of 
.
- Let
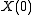be the intersection of the kernels of the 
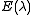. Thus 
is a closed subspace invariant under C and the restriction of C to 
is a compact operator with spectrum {0}.