Special linear Lie algebra
Encyclopedia
In mathematics
, the special linear Lie algebra of order n (denoted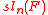
) is the Lie algebra
of
matrices with trace zero and with the Lie bracket 
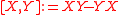. This algebra is well studied and understood, and is often used as a model for the study of other Lie algebras.
Representation Theory of
The simplest non-trivial Lie algebra is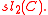 
, consisting of two by two matrices with zero trace. There are three basis elements, 
,
, and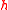 
, with
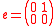
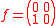
and
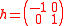
The commutators are
, 
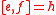, and 
Let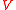
be a finite irreducible representation
of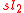
, and let 
be an eigenvector of 
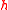with the highest eigenvalue 
. Then,
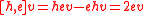
or
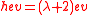
Since
is the eigenvector of highest eigenvalue, 
. Similarly, we can show that
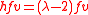
and since h has a lowest eigenvalue, there is a
such that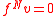 
. We will take the smallest 
such that this happens.
We can then recursively calculate
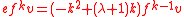
and we find
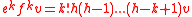
Taking
, we get
Since we chose
to be the smallest exponent such that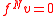 
, we conclude that
. From this, we see that
, 
, ...
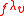
are all nonzero, and it is easy to show that they are linearly independent.
Therefore, for each
, there is a unique, up to isomorphism, irreducible representation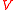 
of dimension 
spanned by elements 
, 
, ...
.
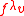The beautiful special case of
shows a general way to find irreducible representations of Lie Algebras. Namely, we divide the algebra to three subalgebras "h" (the Cartan Subalgebra), "e", and "f", which behave approximately like their namesakes in 
. Namely, in a irreducible representation, we have a "highest" eigenvector of "h", on which "e" acts by zero. The basis of the irreducible representation is generated by the action of "f" on the highest eigenvectors of "h".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the special linear Lie algebra of order n (denoted
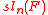) is the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of
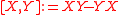matrices with trace zero and with the Lie bracket . This algebra is well studied and understood, and is often used as a model for the study of other Lie algebras. Representation Theory of 
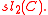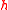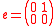
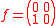
The simplest non-trivial Lie algebra is , consisting of two by two matrices with zero trace. There are three basis elements, ,, and , withand
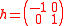
The commutators are
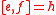, , and Let
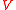be a finite irreducible representationRepresentation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
of
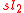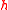, and let be an eigenvector of with the highest eigenvalue . Then,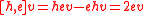or
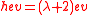
Since
is the eigenvector of highest eigenvalue, . Similarly, we can show that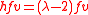and since h has a lowest eigenvalue, there is a
such that 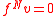. We will take the smallest such that this happens.We can then recursively calculate
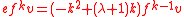
and we find
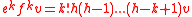
Taking
, we getSince we chose
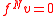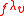
to be the smallest exponent such that , we conclude that. From this, we see that, , ...are all nonzero, and it is easy to show that they are linearly independent.
Therefore, for each
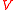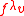, there is a unique, up to isomorphism, irreducible representation of dimension spanned by elements , , ....The beautiful special case of
shows a general way to find irreducible representations of Lie Algebras. Namely, we divide the algebra to three subalgebras "h" (the Cartan Subalgebra), "e", and "f", which behave approximately like their namesakes in . Namely, in a irreducible representation, we have a "highest" eigenvector of "h", on which "e" acts by zero. The basis of the irreducible representation is generated by the action of "f" on the highest eigenvectors of "h".