
Natural deduction
Encyclopedia
In logic
and proof theory
, natural deduction is a kind of proof calculus
in which logical reasoning
is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with the axiomatic system
s which instead use axiom
s as much as possible to express the logical laws of deductive reasoning
.
, Frege
, and Russell
(see, e.g., Hilbert system). Such axiomatizations were most famously used by Russell
and Whitehead
in their mathematical treatise Principia Mathematica
. Spurred on by a series of seminars in Poland in 1926 by Łukasiewicz
that advocated a more natural treatment of logic, Jaśkowski made the earliest attempts at defining a more natural deduction, first in 1929 using a diagrammatic notation, and later updating his proposal in a sequence of papers in 1934 and 1935. His proposals led to different notations
such as Fitch-style calculus
(or Fitch's diagrams) or Suppes
' method of which e.g. Lemmon
gave a variant called system L.
Natural deduction in its modern form was independently proposed by the German mathematician Gentzen
in 1935, in a dissertation delivered to the faculty of mathematical sciences of the university of Göttingen. The term natural deduction (or rather, its German equivalent natürliches Schließen) was coined in that paper:
Gentzen was motivated by a desire to establish the consistency of number theory. He was unable to prove the main result required for the consistency result, the cut elimination theorem - the Hauptsatz - directly for Natural Deduction. For this reason he introduced his alternative system, the sequent calculus
for which he proves the Hauptsatz both for classical and intuitionistic logic. In a series of seminars in 1961 and 1962 Prawitz
gave a comprehensive summary of natural deduction calculi, and transported much of Gentzen's work with sequent calculi into the natural deduction framework. His 1965 monograph Natural deduction: a proof-theoretical study was to become a reference work on natural deduction, and included applications for modal
and second-order logic
.
In natural deduction, a proposition
is deduced from a collection of premises by applying inference rules repeatedly. The system presented in this article is a minor variation of Gentzen's or Prawitz's formulation, but with a closer adherence to Martin-Löf
's description of logical judgments and connectives (Martin-Löf, 1996).
is something that is knowable, that is, an object of knowledge. It is evident if one in fact knows it. Thus "it is raining" is a judgment, which is evident for the one who knows that it is actually raining; in this case one may readily find evidence for the judgment by looking outside the window or stepping out of the house. In mathematical logic however, evidence is often not as directly observable, but rather deduced from more basic evident judgments. The process of deduction is what constitutes a proof; in other words, a judgment is evident if one has a proof for it.
The most important judgments in logic are of the form "A is true". The letter A stands for any expression representing a proposition; the truth judgments thus require a more primitive judgment: "A is a proposition". Many other judgments have been studied; for example, "A is false" (see classical logic
), "A is true at time t" (see temporal logic
), "A is necessarily true" or "A is possibly true" (see modal logic
), "the program M has type τ" (see programming language
s and type theory
), "A is achievable from the available resources" (see linear logic
), and many others. To start with, we shall concern ourselves with the simplest two judgments "A is a proposition" and "A is true", abbreviated as "A prop" and "A true" respectively.
The judgment "A prop" defines the structure of valid proofs of A, which in turn defines the structure of propositions. For this reason, the inference rules for this judgment are sometimes known as formation rules. To illustrate, if we have two propositions A and B (that is, the judgments "A prop" and "B prop" are evident), then we form the compound proposition A and B, written symbolically as " ". We can write this in the form of an inference rule:
". We can write this in the form of an inference rule:
This inference rule is schematic: A and B can be instantiated with any expression. The general form of an inference rule is:
where each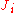 is a judgment and the inference rule is named "name". The judgments above the line are known as premises, and those below the line are conclusions. Other common logical propositions are disjunction (
is a judgment and the inference rule is named "name". The judgments above the line are known as premises, and those below the line are conclusions. Other common logical propositions are disjunction ( ), negation (
), negation (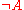 ), implication (
), implication ( ), and the logical constants truth (
), and the logical constants truth ( ) and falsehood (
) and falsehood ( ). Their formation rules are below.
). Their formation rules are below.
It must be understood that in such rules the objects are propositions. That is, the above rule is really an abbreviation for:
This can also be written:
In this form, the first premise can be satisfied by the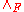 formation rule, giving the first two premises of the previous form. In this article we shall elide the "prop" judgments where they are understood. In the nullary case, one can derive truth from no premises.
formation rule, giving the first two premises of the previous form. In this article we shall elide the "prop" judgments where they are understood. In the nullary case, one can derive truth from no premises.
If the truth of a proposition can be established in more than one way, the corresponding connective has multiple introduction rules.
Note that in the nullary case, i.e., for falsehood, there are no introduction rules. Thus one can never infer falsehood from simpler judgments.
Dual to introduction rules are elimination rules to describe how to de-construct information about a compound proposition into information about its constituents. Thus, from "A ∧ B true", we can conclude "A true" and "B true":
As an example of the use of inference rules, consider commutativity of conjunction. If A ∧ B is true, then B ∧ A is true; This derivation can be drawn by composing inference rules in such a fashion that premises of a lower inference match the conclusion of the next higher inference.
The inference figures we have seen so far are not sufficient to state the rules of implication introduction or disjunction elimination; for these, we need a more general notion of hypothetical derivation.
This derivation does not establish the truth of B as such; rather, it establishes the following fact:
In logic, one says "assuming A ∧ (B ∧ C) is true, we show that B is true"; in other words, the judgement "B true" depends on the assumed judgement "A ∧ (B ∧ C) true". This is a hypothetical derivation, which we write as follows:
The interpretation is: "B true is derivable from A ∧ (B ∧ C) true". Of course, in this specific example we actually know the derivation of "B true" from "A ∧ (B ∧ C) true", but in general we may not a-priori know the derivation. The general form of a hypothetical derivation is:
Each hypothetical derivation has a collection of antecedent derivations (the Di) written on the top line, and a succedent judgement (J) written on the bottom line. Each of the premises may itself be a hypothetical derivation. (For simplicity, we treat a judgement as a premise-less derivation.)
The notion of hypothetical judgement is internalised as the connective of implication. The introduction and elimination rules are as follows.
In the introduction rule, the antecedent named u is discharged in the conclusion. This is a mechanism for delimiting the scope of the hypothesis: its sole reason for existence is to establish "B true"; it cannot be used for any other purpose, and in particular, it cannot be used below the introduction. As an example, consider the derivation of "A ⊃ (B ⊃ (A ∧ B)) true":
This full derivation has no unsatisfied premises; however, sub-derivations are hypothetical. For instance, the derivation of "B ⊃ (A ∧ B) true" is hypothetical with antecedent "A true" (named u).
With hypothetical derivations, we can now write the elimination rule for disjunction:
In words, if A ∨ B is true, and we can derive C true both from A true and from B true, then C is indeed true. Note that this rule does not commit to either A true or B true. In the zero-ary case, i.e. for falsehood, we obtain the following elimination rule:
This is read as: if falsehood is true, then any proposition C is true.
Negation is similar to implication.
The introduction rule discharges both the name of the hypothesis u, and the succedent p, i.e., the proposition p must not occur in the conclusion A. Since these rules are schematic, the interpretation of the introduction rule is: if from "A true" we can derive for every proposition p that "p true", then A must be false, i.e., "not A true". For the elimination, if both A and not A are shown to be true, then there is a contradiction, in which case every proposition C is true. Because the rules for implication and negation are so similar, it should be fairly easy to see that not A and A ⊃ ⊥ are equivalent, i.e., each is derivable from the other.
. However, there are local notions of consistency and completeness that are purely syntactic checks on the inference rules, and require no appeals to models. The first of these is local consistency, also known as local reducibility, which says that any derivation containing an introduction of a connective followed immediately by its elimination can be turned into an equivalent derivation without this detour. It is a check on the strength of elimination rules: they must not be so strong that they include knowledge not already contained in its premises. As an example, consider conjunctions.
Dually, local completeness says that the elimination rules are strong enough to decompose a connective into the forms suitable for its introduction rule. Again for conjunctions:
These notions correspond exactly to β-reduction (beta reduction) and η-conversion (eta conversion) in the lambda calculus
, using the Curry–Howard isomorphism. By local completeness, we see that every derivation can be converted to an equivalent derivation where the principal connective is introduced. In fact, if the entire derivation obeys this ordering of eliminations followed by introductions, then it is said to be normal. In a normal derivation all eliminations happen above introductions. In most logics, every derivation has an equivalent normal derivation, called a normal form. The existence of normal forms is generally hard to prove using natural deduction alone, though such accounts do exist in the literature, most notably by Dag Prawitz
in 1961; see his book Natural deduction: a proof-theoretical study, A&W Stockholm 1965, no ISBN. It is much easier to show this indirectly by means of a cut-free sequent calculus
presentation.
For propositions, we consider a third countable set P of predicates, and define atomic predicates over terms with the following formation rule:
In addition, we add a pair of quantified propositions: universal (∀) and existential (∃):
These quantified propositions have the following introduction and elimination rules.
In these rules, the notation [t/x] A stands for the substitution of t for every (visible) instance of x in A, avoiding capture; see the article on lambda calculus
for more detail about this standard operation. As before the superscripts on the name stand for the components that are discharged: the term a cannot occur in the conclusion of ∀I (such terms are known as eigenvariables or parameters), and the hypotheses named u and v in ∃E are localised to the second premise in a hypothetical derivation. Although the propositional logic of earlier sections was decidable
, adding the quantifiers makes the logic undecidable.
So far the quantified extensions are first-order: they distinguish propositions from the kinds of objects quantified over. Higher-order logic takes a different approach and has only a single sort of propositions. The quantifiers have as the domain of quantification the very same sort of propositions, as reflected in the formation rules:
A discussion of the introduction and elimination forms for higher-order logic is beyond the scope of this article. It is possible to be in between first-order and higher-order logics. For example, second-order logic has two kinds of propositions, one kind quantifying over terms, and the second kind quantifying over propositions of the first kind.
(or Fitch's diagrams) or Suppes
' method of which e.g. Lemmon
gave a variant called system L.
. This modification sometimes goes under the name of localised hypotheses. The following diagram summarises the change.
The collection of hypotheses will be written as Γ when their exact composition is not relevant.
To make proofs explicit, we move from the proof-less judgement "A true" to a judgement: "π is a proof of (A true)", which is written symbolically as "π : A true". Following the standard approach, proofs are specified with their own formation rules for the judgement "π proof". The simplest possible proof is the use of a labelled hypothesis; in this case the evidence is the label itself.
For brevity, we shall leave off the judgemental label true in the rest of this article, i.e., write "Γ π : A". Let us re-examine some of the connectives with explicit proofs. For conjunction, we look at the introduction rule ∧I to discover the form of proofs of conjunction: they must be a pair of proofs of the two conjuncts. Thus:
The elimination rules ∧E1 and ∧E2 select either the left or the right conjunct; thus the proofs are a pair of projections — first (fst) and second (snd).
For implication, the introduction form localises or binds the hypothesis, written using a λ; this corresponds to the discharged label. In the rule, "Γ, u:A" stands for the collection of hypotheses Γ, together with the additional hypothesis u.
With proofs available explicitly, one can manipulate and reason about proofs. The key operation on proofs is the substitution of one proof for an assumption used in another proof. This is commonly known as a substitution theorem, and can be proved by induction
on the depth (or structure) of the second judgement.
Substitution theorem : If Γ π1 : A and Γ, u:A π2 : B, then Γ [π1/u] π2 : B.
So far the judgement "Γ π : A" has had a purely logical interpretation. In type theory
, the logical view is exchanged for a more computational view of objects. Propositions in the logical interpretation are now viewed as types, and proofs as programs in the lambda calculus
. Thus the interpretation of "π : A" is "the program π has type A". The logical connectives are also given a different reading: conjunction is viewed as product (×), implication as the function arrow (→), etc. The differences are only cosmetic, however. Type theory has a natural deduction presentation in terms of formation, introduction and elimination rules; in fact, the reader can easily reconstruct what is known as simple type theory from the previous sections.
The difference between logic and type theory is primarily a shift of focus from the types (propositions) to the programs (proofs). Type theory is chiefly interested in the convertibility or reducibility of programs. For every type, there are canonical programs of that type which are irreducible; these are known as canonical forms or values. If every program can be reduced to a canonical form, then the type theory is said to be normalising (or weakly normalising). If the canonical form is unique, then the theory is said to be strongly normalising. Normalisability is a rare feature of most non-trivial type theories, which is a big departure from the logical world. (Recall that every logical derivation has an equivalent normal derivation.) To sketch the reason: in type theories that admit recursive definitions, it is possible to write programs that never reduce to a value; such looping programs can generally be given any type. In particular, the looping program has type ⊥, although there is no logical proof of "⊥ true". For this reason, the propositions as types; proofs as programs paradigm only works in one direction, if at all: interpreting a type theory as a logic generally gives an inconsistent logic.
Like logic, type theory has many extensions and variants, including first-order and higher-order versions. An interesting branch of type theory, known as dependent type theory, allows quantifiers to range over programs themselves. These quantified types are written as Π and Σ instead of ∀ and ∃, and have the following formation rules:
These types are generalisations of the arrow and product types, respectively, as witnessed by their introduction and elimination rules.
Dependent type theory in full generality is very powerful: it is able to express almost any conceivable property of programs directly in the types of the program. This generality comes at a steep price — checking that a given program is of a given type is undecidable. For this reason, dependent type theories in practice do not allow quantification over arbitrary programs, but rather restrict to programs of a given decidable index domain, for example integers, strings, or linear programs.
Since dependent type theories allow types to depend on programs, a natural question to ask is whether it is possible for programs to depend on types, or any other combination. There are many kinds of answers to such questions. A popular approach in type theory is to allow programs to be quantified over types, also known as parametric polymorphism; of this there are two main kinds: if types and programs are kept separate, then one obtains a somewhat more well-behaved system called predicative polymorphism; if the distinction between program and type is blurred, one obtains the type-theoretic analogue of higher-order logic, also known as impredicative polymorphism. Various combinations of dependency and polymorphism have been considered in the literature, the most famous being the lambda cube
of Henk Barendregt
.
The intersection of logic and type theory is a vast and active research area. New logics are usually formalised in a general type theoretic setting, known as a logical framework. Popular modern logical frameworks such as the calculus of constructions
and LF
are based on higher-order dependent type theory, with various trade-offs in terms of decidability and expressive power. These logical frameworks are themselves always specified as natural deduction systems, which is a testament to the versatility of the natural deduction approach.
. Classical logic
extends intuitionistic logic with an additional axiom
or principle of excluded middle:
This statement is not obviously either an introduction or an elimination; indeed, it involves two distinct connectives. Gentzen's original treatment of excluded middle prescribed one of the following three (equivalent) formulations, which were already present in analogous forms in the systems of Hilbert
and Heyting
:
(XM3 is merely XM2 expressed in terms of E.) This treatment of excluded middle, in addition to being objectionable from a purist's standpoint, introduces additional complications in the definition of normal forms.
A comparatively more satisfactory treatment of classical natural deduction in terms of introduction and elimination rules alone was first proposed by Parigot in 1992 in the form of a classical lambda calculus
called λμ
. The key insight of his approach was to replace a truth-centric judgement A true with a more classical notion, reminiscent of the sequent calculus
: in localised form, instead of Γ A, he used Γ Δ, with Δ a collection of propositions similar to Γ. Γ was treated as a conjunction, and Δ as a disjunction. This structure is essentially lifted directly from classical sequent calculi
, but the innovation in λμ was to give a computational meaning to classical natural deduction proofs in terms of a callcc or a throw/catch mechanism seen in LISP
and its descendants. (See also: first class control.)
Another important extension was for modal
and other logics that need more than just the basic judgement of truth. These were first described, for the alethic modal logics S4 and S5, in a natural deduction style by Prawitz
in 1965, and have since accumulated a large body of related work. To give a simple example, the modal logic S4 requires one new judgement, "A valid", that is categorical with respect to truth:
This categorical judgement is internalised as a unary connective A (read "necessarily A") with the following introduction and elimination rules:
Note that the premise "A valid" has no defining rules; instead, the categorical definition of validity is used in its place. This mode becomes clearer in the localised form when the hypotheses are explicit. We write "Ω;Γ A true" where Γ contains the true hypotheses as before, and Ω contains valid hypotheses. On the right there is just a single judgement "A true"; validity is not needed here since "Ω A valid" is by definition the same as "Ω; A true". The introduction and elimination forms are then:
The modal hypotheses have their own version of the hypothesis rule and substitution theorem.
Modal substitution theorem : If Ω; π1 : A true and Ω, u: (A valid) ; Γ π2 : C true, then Ω;Γ [π1/u] π2 : C true.
This framework of separating judgements into distinct collections of hypotheses, also known as multi-zoned or polyadic contexts, is very powerful and extensible; it has been applied for many different modal logics, and also for linear
and other substructural logic
s, to give a few examples. However, relatively few systems of modal logic can be formalised directly in natural deduction. To give proof-theoretic characterisations of these systems, extensions such as labelling or systems of deep inference.
The addition of labels to formulae permits much finer control of the conditions under which rules apply, allowing the more flexible techniques of analytic tableaux to be applied, as has been done in the case of labelled deduction. Labels also allow the naming of worlds in Kripke semantics; Simpson (1993) presents an influential technique for converting frame conditions of modal logics in Kripke semantics into inference rules in a natural deduction formalisation of hybrid logic
. Stouppa (2004) surveys the application of many proof theories, such as Avron and Pottinger's hypersequents and Belnap's display logic to such modal logics as S5 and B.
. In natural deduction the flow of information is bi-directional: elimination rules flow information downwards by deconstruction, and introduction rules flow information upwards by assembly. Thus, a natural deduction proof does not have a purely bottom-up or top-down reading, making it unsuitable for automation in proof search, or even for proof checking (or type-checking in type theory). To address this fact, Gentzen
in 1935 proposed his sequent calculus
, though he initially intended it as a technical device for clarifying the consistency of predicate logic
. Kleene
, in his seminal 1952 book Introduction to Metamathematics (ISBN 0-7204-2103-9), gave the first formulation of the sequent calculus in the modern style.
In the sequent calculus all inference rules have a purely bottom-up reading. Inference rules can apply to elements on both sides of the turnstile
. (To differentiate from natural deduction, this article uses a double arrow ⇒ instead of the right tack for sequents.) The introduction rules of natural deduction are viewed as right rules in the sequent calculus, and are structurally very similar. The elimination rules on the other hand turn into left rules in the sequent calculus. To give an example, consider disjunction; the right rules are familiar:
On the left:
Recall the ∨E rule of natural deduction in localised form:
The proposition A ∨ B, which is the succedent of a premise in ∨E, turns into a hypothesis of the conclusion in the left rule ∨L. Thus, left rules can be seen as a sort of inverted elimination rule. This observation can be illustrated as follows:
In the sequent calculus, the left and right rules are performed in lock-step until one reaches the initial sequent, which corresponds to the meeting point of elimination and introduction rules in natural deduction. These initial rules are superficially similar to the hypothesis rule of natural deduction, but in the sequent calculus they describe a transposition or a handshake of a left and a right proposition:
The correspondence between the sequent calculus and natural deduction is a pair of soundness and completeness theorems, which are both provable by means of an inductive argument.
Soundness of ⇒ wrt. : If Γ ⇒ A, then Γ A.
Completeness of ⇒ wrt. : If Γ A, then Γ ⇒ A.
It is clear by these theorems that the sequent calculus does not change the notion of truth, because the same collection of propositions remain true. Thus, one can use the same proof objects as before in sequent calculus derivations. As an example, consider the conjunctions. The right rule is virtually identical to the introduction rule
The left rule, however, performs some additional substitutions that are not performed in the corresponding elimination rules.
The kinds of proofs generated in the sequent calculus are therefore rather different from those of natural deduction. The sequent calculus produces proofs in what is known as the β-normal η-long form, which corresponds to a canonical representation of the normal form of the natural deduction proof. If one attempts to describe these proofs using natural deduction itself, one obtains what is called the intercalation calculus (first described by John Byrnes [3]), which can be used to formally define the notion of a normal form for natural deduction.
The substitution theorem of natural deduction takes the form of a structural rule
or structural theorem known as cut in the sequent calculus.
Cut (substitution) : If Γ ⇒ π1 : A and Γ, u:A ⇒ π2 : C, then Γ ⇒ [π1/u] π2 : C.
In most well behaved logics, cut is unnecessary as an inference rule, though it remains provable as a meta-theorem; the superfluousness of the cut rule is usually presented as a computational process, known as cut elimination. This has an interesting application for natural deduction; usually it is extremely tedious to prove certain properties directly in natural deduction because of an unbounded number of cases. For example, consider showing that a given proposition is not provable in natural deduction. A simple inductive argument fails because of rules like ∨E or E which can introduce arbitrary propositions. However, we know that the sequent calculus is complete with respect to natural deduction, so it is enough to show this unprovability in the sequent calculus. Now, if cut is not available as an inference rule, then all sequent rules either introduce a connective on the right or the left, so the depth of a sequent derivation is fully bounded by the connectives in the final conclusion. Thus, showing unprovability is much easier, because there are only a finite number of cases to consider, and each case is composed entirely of sub-propositions of the conclusion. A simple instance of this is the global consistency theorem: " ⊥ true" is not provable. In the sequent calculus version, this is manifestly true because there is no rule that can have " ⇒ ⊥" as a conclusion! Proof theorists often prefer to work on cut-free sequent calculus formulations because of such properties.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
, natural deduction is a kind of proof calculus
Proof calculus
In mathematical logic, a proof calculus corresponds to a family of formal systems that use a common style of formal inference for its inference rules...
in which logical reasoning
Logical reasoning
In logic, three kinds of logical reasoning can be distinguished: deduction, induction and abduction. Given a precondition, a conclusion, and a rule that the precondition implies the conclusion, they can be explained in the following way:...
is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with the axiomatic system
Axiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
s which instead use axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s as much as possible to express the logical laws of deductive reasoning
Deductive reasoning
Deductive reasoning, also called deductive logic, is reasoning which constructs or evaluates deductive arguments. Deductive arguments are attempts to show that a conclusion necessarily follows from a set of premises or hypothesis...
.
Motivation
Natural deduction grew out of a context of dissatisfaction with the axiomatizations of deductive reasoning common to the systems of HilbertDavid Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
, and Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
(see, e.g., Hilbert system). Such axiomatizations were most famously used by Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
and Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
in their mathematical treatise Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
. Spurred on by a series of seminars in Poland in 1926 by Łukasiewicz
Jan Lukasiewicz
Jan Łukasiewicz was a Polish logician and philosopher born in Lwów , Galicia, Austria–Hungary . His work centred on analytical philosophy and mathematical logic...
that advocated a more natural treatment of logic, Jaśkowski made the earliest attempts at defining a more natural deduction, first in 1929 using a diagrammatic notation, and later updating his proposal in a sequence of papers in 1934 and 1935. His proposals led to different notations
such as Fitch-style calculus
Fitch-style calculus
Fitch-style calculus, also known as Fitch diagrams , is a method for constructing formal proofs used in first-order logic. It was invented by American logician Frederic Brenton Fitch...
(or Fitch's diagrams) or Suppes
Patrick Suppes
Patrick Colonel Suppes is an American philosopher who has made significant contributions to philosophy of science, the theory of measurement, the foundations of quantum mechanics, decision theory, psychology, and educational technology...
' method of which e.g. Lemmon
John Lemmon
Edward John Lemmon was a logician and philosopher born in Sheffield, UK. He is most well known for his work on modal logic, particularly his joint text with Dana Scott published posthumously ....
gave a variant called system L.
Natural deduction in its modern form was independently proposed by the German mathematician Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
in 1935, in a dissertation delivered to the faculty of mathematical sciences of the university of Göttingen. The term natural deduction (or rather, its German equivalent natürliches Schließen) was coined in that paper:
Gentzen was motivated by a desire to establish the consistency of number theory. He was unable to prove the main result required for the consistency result, the cut elimination theorem - the Hauptsatz - directly for Natural Deduction. For this reason he introduced his alternative system, the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
for which he proves the Hauptsatz both for classical and intuitionistic logic. In a series of seminars in 1961 and 1962 Prawitz
Dag Prawitz
Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....
gave a comprehensive summary of natural deduction calculi, and transported much of Gentzen's work with sequent calculi into the natural deduction framework. His 1965 monograph Natural deduction: a proof-theoretical study was to become a reference work on natural deduction, and included applications for modal
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
and second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
.
In natural deduction, a proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
is deduced from a collection of premises by applying inference rules repeatedly. The system presented in this article is a minor variation of Gentzen's or Prawitz's formulation, but with a closer adherence to Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
's description of logical judgments and connectives (Martin-Löf, 1996).
Judgments and propositions
A judgmentJudgment (mathematical logic)
In mathematical logic, a judgment can be for example an assertion about occurrence of a free variable in an expression of the object language, or about provability of a proposition ; but judgments can be also other inductively definable assertions in the metatheory...
is something that is knowable, that is, an object of knowledge. It is evident if one in fact knows it. Thus "it is raining" is a judgment, which is evident for the one who knows that it is actually raining; in this case one may readily find evidence for the judgment by looking outside the window or stepping out of the house. In mathematical logic however, evidence is often not as directly observable, but rather deduced from more basic evident judgments. The process of deduction is what constitutes a proof; in other words, a judgment is evident if one has a proof for it.
The most important judgments in logic are of the form "A is true". The letter A stands for any expression representing a proposition; the truth judgments thus require a more primitive judgment: "A is a proposition". Many other judgments have been studied; for example, "A is false" (see classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
), "A is true at time t" (see temporal logic
Temporal logic
In logic, the term temporal logic is used to describe any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time. In a temporal logic we can then express statements like "I am always hungry", "I will eventually be hungry", or "I will be hungry...
), "A is necessarily true" or "A is possibly true" (see modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
), "the program M has type τ" (see programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s and type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
), "A is achievable from the available resources" (see linear logic
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
), and many others. To start with, we shall concern ourselves with the simplest two judgments "A is a proposition" and "A is true", abbreviated as "A prop" and "A true" respectively.
The judgment "A prop" defines the structure of valid proofs of A, which in turn defines the structure of propositions. For this reason, the inference rules for this judgment are sometimes known as formation rules. To illustrate, if we have two propositions A and B (that is, the judgments "A prop" and "B prop" are evident), then we form the compound proposition A and B, written symbolically as "
 ". We can write this in the form of an inference rule:
". We can write this in the form of an inference rule:This inference rule is schematic: A and B can be instantiated with any expression. The general form of an inference rule is:
where each
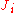 is a judgment and the inference rule is named "name". The judgments above the line are known as premises, and those below the line are conclusions. Other common logical propositions are disjunction (
is a judgment and the inference rule is named "name". The judgments above the line are known as premises, and those below the line are conclusions. Other common logical propositions are disjunction ( ), negation (
), negation (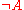 ), implication (
), implication ( ), and the logical constants truth (
), and the logical constants truth ( ) and falsehood (
) and falsehood ( ). Their formation rules are below.
). Their formation rules are below.Introduction and elimination
Now we discuss the "A true" judgment. Inference rules that introduce a logical connective in the conclusion are known as introduction rules. To introduce conjunctions, i.e., to conclude "A and B true" for propositions A and B, one requires evidence for "A true" and "B true". As an inference rule:It must be understood that in such rules the objects are propositions. That is, the above rule is really an abbreviation for:
This can also be written:
In this form, the first premise can be satisfied by the
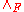 formation rule, giving the first two premises of the previous form. In this article we shall elide the "prop" judgments where they are understood. In the nullary case, one can derive truth from no premises.
formation rule, giving the first two premises of the previous form. In this article we shall elide the "prop" judgments where they are understood. In the nullary case, one can derive truth from no premises.If the truth of a proposition can be established in more than one way, the corresponding connective has multiple introduction rules.
Note that in the nullary case, i.e., for falsehood, there are no introduction rules. Thus one can never infer falsehood from simpler judgments.
Dual to introduction rules are elimination rules to describe how to de-construct information about a compound proposition into information about its constituents. Thus, from "A ∧ B true", we can conclude "A true" and "B true":
As an example of the use of inference rules, consider commutativity of conjunction. If A ∧ B is true, then B ∧ A is true; This derivation can be drawn by composing inference rules in such a fashion that premises of a lower inference match the conclusion of the next higher inference.
The inference figures we have seen so far are not sufficient to state the rules of implication introduction or disjunction elimination; for these, we need a more general notion of hypothetical derivation.
Hypothetical derivations
A pervasive operation in mathematical logic is reasoning from assumptions. For example, consider the following derivation:This derivation does not establish the truth of B as such; rather, it establishes the following fact:
- If A ∧ (B ∧ C) is true then B is true.
In logic, one says "assuming A ∧ (B ∧ C) is true, we show that B is true"; in other words, the judgement "B true" depends on the assumed judgement "A ∧ (B ∧ C) true". This is a hypothetical derivation, which we write as follows:
The interpretation is: "B true is derivable from A ∧ (B ∧ C) true". Of course, in this specific example we actually know the derivation of "B true" from "A ∧ (B ∧ C) true", but in general we may not a-priori know the derivation. The general form of a hypothetical derivation is:
Each hypothetical derivation has a collection of antecedent derivations (the Di) written on the top line, and a succedent judgement (J) written on the bottom line. Each of the premises may itself be a hypothetical derivation. (For simplicity, we treat a judgement as a premise-less derivation.)
The notion of hypothetical judgement is internalised as the connective of implication. The introduction and elimination rules are as follows.
In the introduction rule, the antecedent named u is discharged in the conclusion. This is a mechanism for delimiting the scope of the hypothesis: its sole reason for existence is to establish "B true"; it cannot be used for any other purpose, and in particular, it cannot be used below the introduction. As an example, consider the derivation of "A ⊃ (B ⊃ (A ∧ B)) true":
This full derivation has no unsatisfied premises; however, sub-derivations are hypothetical. For instance, the derivation of "B ⊃ (A ∧ B) true" is hypothetical with antecedent "A true" (named u).
With hypothetical derivations, we can now write the elimination rule for disjunction:
In words, if A ∨ B is true, and we can derive C true both from A true and from B true, then C is indeed true. Note that this rule does not commit to either A true or B true. In the zero-ary case, i.e. for falsehood, we obtain the following elimination rule:
This is read as: if falsehood is true, then any proposition C is true.
Negation is similar to implication.
The introduction rule discharges both the name of the hypothesis u, and the succedent p, i.e., the proposition p must not occur in the conclusion A. Since these rules are schematic, the interpretation of the introduction rule is: if from "A true" we can derive for every proposition p that "p true", then A must be false, i.e., "not A true". For the elimination, if both A and not A are shown to be true, then there is a contradiction, in which case every proposition C is true. Because the rules for implication and negation are so similar, it should be fairly easy to see that not A and A ⊃ ⊥ are equivalent, i.e., each is derivable from the other.
Consistency, completeness, and normal forms
A theory is said to be consistent if falsehood is not provable (from no assumptions) and is complete if every theorem is provable using the inference rules of the logic. These are statements about the entire logic, and are usually tied to some notion of a modelModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
. However, there are local notions of consistency and completeness that are purely syntactic checks on the inference rules, and require no appeals to models. The first of these is local consistency, also known as local reducibility, which says that any derivation containing an introduction of a connective followed immediately by its elimination can be turned into an equivalent derivation without this detour. It is a check on the strength of elimination rules: they must not be so strong that they include knowledge not already contained in its premises. As an example, consider conjunctions.
------ u ------ w A true B true ------------------ ∧I A ∧ B true ---------- ∧E1 A true | ⇒ | ------ u A true |
Dually, local completeness says that the elimination rules are strong enough to decompose a connective into the forms suitable for its introduction rule. Again for conjunctions:
---------- u A ∧ B true | ⇒ | ---------- u ---------- u A ∧ B true A ∧ B true ---------- ∧E1 ---------- ∧E2 A true B true ----------------------- ∧I A ∧ B true |
These notions correspond exactly to β-reduction (beta reduction) and η-conversion (eta conversion) in the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, using the Curry–Howard isomorphism. By local completeness, we see that every derivation can be converted to an equivalent derivation where the principal connective is introduced. In fact, if the entire derivation obeys this ordering of eliminations followed by introductions, then it is said to be normal. In a normal derivation all eliminations happen above introductions. In most logics, every derivation has an equivalent normal derivation, called a normal form. The existence of normal forms is generally hard to prove using natural deduction alone, though such accounts do exist in the literature, most notably by Dag Prawitz
Dag Prawitz
Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....
in 1961; see his book Natural deduction: a proof-theoretical study, A&W Stockholm 1965, no ISBN. It is much easier to show this indirectly by means of a cut-free sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
presentation.
First and higher-order extensions
The logic of the earlier section is an example of a single-sorted logic, i.e., a logic with a single kind of object: propositions. Many extensions of this simple framework have been proposed; in this section we will extend it with a second sort of individuals or terms. More precisely, we will add a new kind of judgement, "t is a term" (or "t term") where t is schematic. We shall fix a countable set V of variables, another countable set F of function symbols, and construct terms as follows:v ∈ V ------ var-F v term | f ∈ F t1 term t2 term ... tn term ------------------------------------------ app-F f (t1, t2, ..., tn) term |
For propositions, we consider a third countable set P of predicates, and define atomic predicates over terms with the following formation rule:
φ ∈ P t1 term t2 term ... tn term ------------------------------------------ pred-F φ (t1, t2, ..., tn) prop |
In addition, we add a pair of quantified propositions: universal (∀) and existential (∃):
------ u x term A prop ---------- ∀Fu ∀x. A prop | ------ u x term A prop ---------- ∃Fu ∃x. A prop |
These quantified propositions have the following introduction and elimination rules.
------ u a term [a/x] A true ------------ ∀Iu, a ∀x. A true | ∀x. A true t term -------------------- ∀E [t/x] A true | |
[t/x] A true ------------ ∃I ∃x. A true | ------ u ------------ v a term [a/x] A true ∃x. A true C true -------------------------- ∃Ea, u,v C true |
In these rules, the notation [t/x] A stands for the substitution of t for every (visible) instance of x in A, avoiding capture; see the article on lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
for more detail about this standard operation. As before the superscripts on the name stand for the components that are discharged: the term a cannot occur in the conclusion of ∀I (such terms are known as eigenvariables or parameters), and the hypotheses named u and v in ∃E are localised to the second premise in a hypothetical derivation. Although the propositional logic of earlier sections was decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
, adding the quantifiers makes the logic undecidable.
So far the quantified extensions are first-order: they distinguish propositions from the kinds of objects quantified over. Higher-order logic takes a different approach and has only a single sort of propositions. The quantifiers have as the domain of quantification the very same sort of propositions, as reflected in the formation rules:
------ u p prop A prop ---------- ∀Fu ∀p. A prop | ------ u p prop A prop ---------- ∃Fu ∃p. A prop |
A discussion of the introduction and elimination forms for higher-order logic is beyond the scope of this article. It is possible to be in between first-order and higher-order logics. For example, second-order logic has two kinds of propositions, one kind quantifying over terms, and the second kind quantifying over propositions of the first kind.
Tree-like presentations
Gentzen's discharging annotations used to internalise hypothetical judgment can be avoided by representing proofs as a tree of sequents Γ A instead of a tree of A true judgments.Sequential presentations
Jaśkowski's representations of natural deduction led to different notations such as Fitch-style calculusFitch-style calculus
Fitch-style calculus, also known as Fitch diagrams , is a method for constructing formal proofs used in first-order logic. It was invented by American logician Frederic Brenton Fitch...
(or Fitch's diagrams) or Suppes
Patrick Suppes
Patrick Colonel Suppes is an American philosopher who has made significant contributions to philosophy of science, the theory of measurement, the foundations of quantum mechanics, decision theory, psychology, and educational technology...
' method of which e.g. Lemmon
John Lemmon
Edward John Lemmon was a logician and philosopher born in Sheffield, UK. He is most well known for his work on modal logic, particularly his joint text with Dana Scott published posthumously ....
gave a variant called system L.
Proofs and type-theory
The presentation of natural deduction so far has concentrated on the nature of propositions without giving a formal definition of a proof. To formalise the notion of proof, we alter the presentation of hypothetical derivations slightly. We label the antecedents with proof variables (from some countable set V of variables), and decorate the succedent with the actual proof. The antecedents or hypotheses are separated from the succedent by means of a turnstileTurnstile (symbol)
In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
. This modification sometimes goes under the name of localised hypotheses. The following diagram summarises the change.
---- u1 ---- u2 ... ---- un J1 J2 Jn J | ⇒ | u1:J1, u2:J2, ..., un:Jn J |
The collection of hypotheses will be written as Γ when their exact composition is not relevant.
To make proofs explicit, we move from the proof-less judgement "A true" to a judgement: "π is a proof of (A true)", which is written symbolically as "π : A true". Following the standard approach, proofs are specified with their own formation rules for the judgement "π proof". The simplest possible proof is the use of a labelled hypothesis; in this case the evidence is the label itself.
u ∈ V ------- proof-F u proof | --------------------- hyp u:A true u : A true |
For brevity, we shall leave off the judgemental label true in the rest of this article, i.e., write "Γ π : A". Let us re-examine some of the connectives with explicit proofs. For conjunction, we look at the introduction rule ∧I to discover the form of proofs of conjunction: they must be a pair of proofs of the two conjuncts. Thus:
π1 proof π2 proof -------------------- pair-F (π1, π2) proof | Γ π1 : A Γ π2 : B ------------------------ ∧I Γ (π1, π2) : A ∧ B |
The elimination rules ∧E1 and ∧E2 select either the left or the right conjunct; thus the proofs are a pair of projections — first (fst) and second (snd).
π proof ----------- fst-F fst π proof | Γ π : A ∧ B ------------- ∧E1 Γ fst π : A | |
π proof ----------- snd-F snd π proof | Γ π : A ∧ B ------------- ∧E2 Γ snd π : B |
For implication, the introduction form localises or binds the hypothesis, written using a λ; this corresponds to the discharged label. In the rule, "Γ, u:A" stands for the collection of hypotheses Γ, together with the additional hypothesis u.
π proof ------------ λ-F λu. π proof | Γ, u:A π : B ----------------- ⊃I Γ λu. π : A ⊃ B | |
π1 proof π2 proof ------------------- app-F π1 π2 proof | Γ π1 : A ⊃ B Γ π2 : A ---------------------------- ⊃E Γ π1 π2 : B |
With proofs available explicitly, one can manipulate and reason about proofs. The key operation on proofs is the substitution of one proof for an assumption used in another proof. This is commonly known as a substitution theorem, and can be proved by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on the depth (or structure) of the second judgement.
Substitution theorem : If Γ π1 : A and Γ, u:A π2 : B, then Γ [π1/u] π2 : B.
So far the judgement "Γ π : A" has had a purely logical interpretation. In type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, the logical view is exchanged for a more computational view of objects. Propositions in the logical interpretation are now viewed as types, and proofs as programs in the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
. Thus the interpretation of "π : A" is "the program π has type A". The logical connectives are also given a different reading: conjunction is viewed as product (×), implication as the function arrow (→), etc. The differences are only cosmetic, however. Type theory has a natural deduction presentation in terms of formation, introduction and elimination rules; in fact, the reader can easily reconstruct what is known as simple type theory from the previous sections.
The difference between logic and type theory is primarily a shift of focus from the types (propositions) to the programs (proofs). Type theory is chiefly interested in the convertibility or reducibility of programs. For every type, there are canonical programs of that type which are irreducible; these are known as canonical forms or values. If every program can be reduced to a canonical form, then the type theory is said to be normalising (or weakly normalising). If the canonical form is unique, then the theory is said to be strongly normalising. Normalisability is a rare feature of most non-trivial type theories, which is a big departure from the logical world. (Recall that every logical derivation has an equivalent normal derivation.) To sketch the reason: in type theories that admit recursive definitions, it is possible to write programs that never reduce to a value; such looping programs can generally be given any type. In particular, the looping program has type ⊥, although there is no logical proof of "⊥ true". For this reason, the propositions as types; proofs as programs paradigm only works in one direction, if at all: interpreting a type theory as a logic generally gives an inconsistent logic.
Like logic, type theory has many extensions and variants, including first-order and higher-order versions. An interesting branch of type theory, known as dependent type theory, allows quantifiers to range over programs themselves. These quantified types are written as Π and Σ instead of ∀ and ∃, and have the following formation rules:
Γ A type Γ, x:A B type ----------------------------- Π-F Γ Πx:A. B type | Γ A type Γ, x:A B type ---------------------------- Σ-F Γ Σx:A. B type |
These types are generalisations of the arrow and product types, respectively, as witnessed by their introduction and elimination rules.
Γ, x:A π : B -------------------- ΠI Γ λx. π : Πx:A. B | Γ π1 : Πx:A. B Γ π2 : A ----------------------------- ΠE Γ π1 π2 : [π2/x] B |
Γ π1 : A Γ, x:A π2 : B ----------------------------- ΣI Γ (π1, π2) : Σx:A. B | Γ π : Σx:A. B ---------------- ΣE1 Γ fst π : A | Γ π : Σx:A. B ------------------------ ΣE2 Γ snd π : [fst π/x] B |
Dependent type theory in full generality is very powerful: it is able to express almost any conceivable property of programs directly in the types of the program. This generality comes at a steep price — checking that a given program is of a given type is undecidable. For this reason, dependent type theories in practice do not allow quantification over arbitrary programs, but rather restrict to programs of a given decidable index domain, for example integers, strings, or linear programs.
Since dependent type theories allow types to depend on programs, a natural question to ask is whether it is possible for programs to depend on types, or any other combination. There are many kinds of answers to such questions. A popular approach in type theory is to allow programs to be quantified over types, also known as parametric polymorphism; of this there are two main kinds: if types and programs are kept separate, then one obtains a somewhat more well-behaved system called predicative polymorphism; if the distinction between program and type is blurred, one obtains the type-theoretic analogue of higher-order logic, also known as impredicative polymorphism. Various combinations of dependency and polymorphism have been considered in the literature, the most famous being the lambda cube
Lambda cube
In mathematical logic and type theory, the λ-cube is a framework for exploring the axes of refinement in Coquand's calculus of constructions, starting from the simply typed lambda calculus as the vertex of a cube placed at the origin, and the calculus of constructions as its diametrically opposite...
of Henk Barendregt
Henk Barendregt
Hendrik Pieter Barendregt is a Dutch logician, known for his work in lambda calculus and type theory.Barendregt studied mathematical logic at Utrecht University, obtaining his Masters in 1968 and his Ph.D. in 1971, both cum laude, under Dirk van Dalen and Georg Kreisel...
.
The intersection of logic and type theory is a vast and active research area. New logics are usually formalised in a general type theoretic setting, known as a logical framework. Popular modern logical frameworks such as the calculus of constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
and LF
LF (logical framework)
In logic, a logical framework provides a means to define a logic as a signature in a higher-order type theory in such a way that provability of a formula in the original logic reduces to a type inhabitation problem in the framework type theory. This approach has been used successfully for ...
are based on higher-order dependent type theory, with various trade-offs in terms of decidability and expressive power. These logical frameworks are themselves always specified as natural deduction systems, which is a testament to the versatility of the natural deduction approach.
Classical and modal logics
For simplicity, the logics presented so far have been intuitionisticIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. Classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
extends intuitionistic logic with an additional axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
or principle of excluded middle:
- For any proposition p, the proposition p ∨ ¬p is true.
This statement is not obviously either an introduction or an elimination; indeed, it involves two distinct connectives. Gentzen's original treatment of excluded middle prescribed one of the following three (equivalent) formulations, which were already present in analogous forms in the systems of Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and Heyting
Arend Heyting
Arend Heyting was a Dutch mathematician and logician. He was a student of Luitzen Egbertus Jan Brouwer at the University of Amsterdam, and did much to put intuitionistic logic on a footing where it could become part of mathematical logic...
:
-------------- XM1 A ∨ ¬A true | ¬¬A true ---------- XM2 A true | -------- u ¬A true p true ------ XM3u, p A true |
(XM3 is merely XM2 expressed in terms of E.) This treatment of excluded middle, in addition to being objectionable from a purist's standpoint, introduces additional complications in the definition of normal forms.
A comparatively more satisfactory treatment of classical natural deduction in terms of introduction and elimination rules alone was first proposed by Parigot in 1992 in the form of a classical lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
called λμ
Lambda-mu calculus
In mathematical logic and computer science, the lambda-mu calculus is an extension of the lambda calculus, and was introduced by M. Parigot. It introduces two new operators: the mu operator and the bracket operator...
. The key insight of his approach was to replace a truth-centric judgement A true with a more classical notion, reminiscent of the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
: in localised form, instead of Γ A, he used Γ Δ, with Δ a collection of propositions similar to Γ. Γ was treated as a conjunction, and Δ as a disjunction. This structure is essentially lifted directly from classical sequent calculi
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, but the innovation in λμ was to give a computational meaning to classical natural deduction proofs in terms of a callcc or a throw/catch mechanism seen in LISP
Lisp
A lisp is a speech impediment, historically also known as sigmatism. Stereotypically, people with a lisp are unable to pronounce sibilants , and replace them with interdentals , though there are actually several kinds of lisp...
and its descendants. (See also: first class control.)
Another important extension was for modal
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
and other logics that need more than just the basic judgement of truth. These were first described, for the alethic modal logics S4 and S5, in a natural deduction style by Prawitz
Dag Prawitz
Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....
in 1965, and have since accumulated a large body of related work. To give a simple example, the modal logic S4 requires one new judgement, "A valid", that is categorical with respect to truth:
- If "A true" under no assumptions of the form "B true", then "A valid".
This categorical judgement is internalised as a unary connective A (read "necessarily A") with the following introduction and elimination rules:
A valid -------- I A true | A true -------- E A true |
Note that the premise "A valid" has no defining rules; instead, the categorical definition of validity is used in its place. This mode becomes clearer in the localised form when the hypotheses are explicit. We write "Ω;Γ A true" where Γ contains the true hypotheses as before, and Ω contains valid hypotheses. On the right there is just a single judgement "A true"; validity is not needed here since "Ω A valid" is by definition the same as "Ω; A true". The introduction and elimination forms are then:
Ω; π : A true -------------------- I Ω; box π : A true | Ω;Γ π : A true ---------------------- E Ω;Γ unbox π : A true |
The modal hypotheses have their own version of the hypothesis rule and substitution theorem.
------------------------------- valid-hyp Ω, u: (A valid) ; Γ u : A true |
Modal substitution theorem : If Ω; π1 : A true and Ω, u: (A valid) ; Γ π2 : C true, then Ω;Γ [π1/u] π2 : C true.
This framework of separating judgements into distinct collections of hypotheses, also known as multi-zoned or polyadic contexts, is very powerful and extensible; it has been applied for many different modal logics, and also for linear
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
and other substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
s, to give a few examples. However, relatively few systems of modal logic can be formalised directly in natural deduction. To give proof-theoretic characterisations of these systems, extensions such as labelling or systems of deep inference.
The addition of labels to formulae permits much finer control of the conditions under which rules apply, allowing the more flexible techniques of analytic tableaux to be applied, as has been done in the case of labelled deduction. Labels also allow the naming of worlds in Kripke semantics; Simpson (1993) presents an influential technique for converting frame conditions of modal logics in Kripke semantics into inference rules in a natural deduction formalisation of hybrid logic
Hybrid logic
Hybrid logic refers to a number of extensions to propositional modal logic with more expressive power, though still less than first-order logic. In formal logic, there is a trade-off between expressiveness and computational tractability . The history of hybrid logic began with Arthur Prior's work...
. Stouppa (2004) surveys the application of many proof theories, such as Avron and Pottinger's hypersequents and Belnap's display logic to such modal logics as S5 and B.
Sequent calculus
The sequent calculus is the chief alternative to natural deduction as a foundation of mathematical logicMathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
. In natural deduction the flow of information is bi-directional: elimination rules flow information downwards by deconstruction, and introduction rules flow information upwards by assembly. Thus, a natural deduction proof does not have a purely bottom-up or top-down reading, making it unsuitable for automation in proof search, or even for proof checking (or type-checking in type theory). To address this fact, Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
in 1935 proposed his sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, though he initially intended it as a technical device for clarifying the consistency of predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
. Kleene
Stephen Cole Kleene
Stephen Cole Kleene was an American mathematician who helped lay the foundations for theoretical computer science...
, in his seminal 1952 book Introduction to Metamathematics (ISBN 0-7204-2103-9), gave the first formulation of the sequent calculus in the modern style.
In the sequent calculus all inference rules have a purely bottom-up reading. Inference rules can apply to elements on both sides of the turnstile
Turnstile (symbol)
In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...
. (To differentiate from natural deduction, this article uses a double arrow ⇒ instead of the right tack for sequents.) The introduction rules of natural deduction are viewed as right rules in the sequent calculus, and are structurally very similar. The elimination rules on the other hand turn into left rules in the sequent calculus. To give an example, consider disjunction; the right rules are familiar:
Γ ⇒ A --------- ∨R1 Γ ⇒ A ∨ B | Γ ⇒ B --------- ∨R2 Γ ⇒ A ∨ B |
On the left:
Γ, u:A ⇒ C Γ, v:B ⇒ C --------------------------- ∨L Γ, w: (A ∨ B) ⇒ C |
Recall the ∨E rule of natural deduction in localised form:
Γ A ∨ B Γ, u:A C Γ, v:B C --------------------------------------- ∨E Γ C |
The proposition A ∨ B, which is the succedent of a premise in ∨E, turns into a hypothesis of the conclusion in the left rule ∨L. Thus, left rules can be seen as a sort of inverted elimination rule. This observation can be illustrated as follows:
| natural deduction | sequent calculus | |
|---|---|---|
------ hyp | | elim. rules | ↓ ---------------------- ↑↓ meet ↑ | | intro. rules | conclusion | ⇒ | --------------------------- init ↑ ↑ | | | left rules | right rules | | conclusion |
In the sequent calculus, the left and right rules are performed in lock-step until one reaches the initial sequent, which corresponds to the meeting point of elimination and introduction rules in natural deduction. These initial rules are superficially similar to the hypothesis rule of natural deduction, but in the sequent calculus they describe a transposition or a handshake of a left and a right proposition:
---------- init Γ, u:A ⇒ A |
The correspondence between the sequent calculus and natural deduction is a pair of soundness and completeness theorems, which are both provable by means of an inductive argument.
Soundness of ⇒ wrt. : If Γ ⇒ A, then Γ A.
Completeness of ⇒ wrt. : If Γ A, then Γ ⇒ A.
It is clear by these theorems that the sequent calculus does not change the notion of truth, because the same collection of propositions remain true. Thus, one can use the same proof objects as before in sequent calculus derivations. As an example, consider the conjunctions. The right rule is virtually identical to the introduction rule
| sequent calculus | natural deduction | |
|---|---|---|
Γ ⇒ π1 : A Γ ⇒ π2 : B --------------------------- ∧R Γ ⇒ (π1, π2) : A ∧ B | Γ π1 : A Γ π2 : B ------------------------- ∧I Γ (π1, π2) : A ∧ B |
The left rule, however, performs some additional substitutions that are not performed in the corresponding elimination rules.
| sequent calculus | natural deduction | |
|---|---|---|
Γ, v: (A ∧ B), u:A ⇒ π : C -------------------------------- ∧L1 Γ, v: (A ∧ B) ⇒ [fst v/u] π : C | Γ π : A ∧ B ------------- ∧E1 Γ fst π : A | |
Γ, v: (A ∧ B), u:B ⇒ π : C -------------------------------- ∧L2 Γ, v: (A ∧ B) ⇒ [snd v/u] π : C | Γ π : A ∧ B ------------- ∧E2 Γ snd π : B |
The kinds of proofs generated in the sequent calculus are therefore rather different from those of natural deduction. The sequent calculus produces proofs in what is known as the β-normal η-long form, which corresponds to a canonical representation of the normal form of the natural deduction proof. If one attempts to describe these proofs using natural deduction itself, one obtains what is called the intercalation calculus (first described by John Byrnes [3]), which can be used to formally define the notion of a normal form for natural deduction.
The substitution theorem of natural deduction takes the form of a structural rule
Structural rule
In proof theory, a structural rule is an inference rule that does not refer to any logical connective, but instead operates on the judgements or sequents directly. Structural rules often mimic intended meta-theoretic properties of the logic...
or structural theorem known as cut in the sequent calculus.
Cut (substitution) : If Γ ⇒ π1 : A and Γ, u:A ⇒ π2 : C, then Γ ⇒ [π1/u] π2 : C.
In most well behaved logics, cut is unnecessary as an inference rule, though it remains provable as a meta-theorem; the superfluousness of the cut rule is usually presented as a computational process, known as cut elimination. This has an interesting application for natural deduction; usually it is extremely tedious to prove certain properties directly in natural deduction because of an unbounded number of cases. For example, consider showing that a given proposition is not provable in natural deduction. A simple inductive argument fails because of rules like ∨E or E which can introduce arbitrary propositions. However, we know that the sequent calculus is complete with respect to natural deduction, so it is enough to show this unprovability in the sequent calculus. Now, if cut is not available as an inference rule, then all sequent rules either introduce a connective on the right or the left, so the depth of a sequent derivation is fully bounded by the connectives in the final conclusion. Thus, showing unprovability is much easier, because there are only a finite number of cases to consider, and each case is composed entirely of sub-propositions of the conclusion. A simple instance of this is the global consistency theorem: " ⊥ true" is not provable. In the sequent calculus version, this is manifestly true because there is no rule that can have " ⇒ ⊥" as a conclusion! Proof theorists often prefer to work on cut-free sequent calculus formulations because of such properties.
See also
Historical references
- Stanaslaw Jaśkowski, 1934. On the Rules of Suppositions in Formal Logic.
- Gerhard Gentzen, 1934/5. Untersuchungen uber das logische Schließen (English translation Investigations into Logical Deduction in Szabo)
Textbooks, surveys and co
- Jon BarwiseJon BarwiseKenneth Jon Barwise was an American mathematician, philosopher and logician who proposed some fundamental revisions to the way that logic is understood and used....
and John EtchemendyJohn EtchemendyJohn W. Etchemendy and of Basque descent is Stanford University's twelfth and current Provost. He succeeded John L. Hennessy to the post on September 1, 2000....
, 2000. Language Proof and Logic. CSLI (University of Chicago Press) and New York: Seven Bridges Press. A gentle introduction to first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
via natural deduction, by two first rate logicians. - Jean Gallier's excellent tutorial on Constructive Logic and Typed Lambda-Calculi, ftp://ftp.cis.upenn.edu/pub/papers/gallier/conslog1.ps. Translated and with appendices by Paul Taylor and Yves Lafont. Lecture notes to a short course at Università degli Studi di Siena, April 1983.
Other references
- Alex Simpson, 1993. The Proof Theory and Semantics of Intuitionistic Modal Logic. PhD thesis, University of Edinburgh.
- Phiniki Stouppa, 2004. The Design of Modal Proof Theories: The Case of S5. MSc thesis, University of Dresden.
External links
- Clemente, Daniel, "Introduction to natural deduction."
- Domino On Acid. Natural deduction visualized as a game of dominoes.
- Pelletier, Jeff, "A History of Natural Deduction and Elementary Logic Textbooks."
- Levy, Michel, A Propositional Prover.

