
Sectrix of Maclaurin
Encyclopedia
In geometry
, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin
(named for Colin Maclaurin
), which is a prominent member of the family, and their sectrix
property, which means they can be used to divide an angle into a given number of equal parts. There are special cases are also known as arachnida or araneidans because of their spider
-like shape, and Plateau curves after Joseph Plateau who studied them.
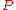 and
and 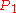 . By translation and rotation we may assume
. By translation and rotation we may assume 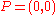 and
and 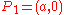 . At time
. At time  , the line rotating about
, the line rotating about 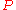 has angle
has angle 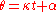 and the line rotating about
and the line rotating about 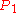 has angle
has angle 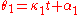 , where
, where  ,
,  ,
, 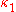 and
and 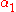 are constants. Eliminate
are constants. Eliminate  to get
to get
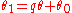 where
where 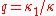 and
and 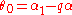 . We assume
. We assume 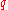 is rational, otherwise the curve is not algebraic and is dense in the plane. Let
is rational, otherwise the curve is not algebraic and is dense in the plane. Let  be the point of intersection of the two lines and let
be the point of intersection of the two lines and let 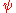 be the angle at
be the angle at  , so
, so 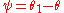 . If
. If  is the distance from
is the distance from 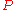 to
to  then, by the law of sines
then, by the law of sines
,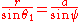
so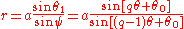
is the equation in polar coordinates.
The case and
and  where
where  is an integer greater than 2 gives arachnida or araneidan curves
is an integer greater than 2 gives arachnida or araneidan curves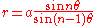
The case and
and 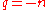 where
where  is an integer greater than 1 gives alternate forms of arachnida or araneidan curves
is an integer greater than 1 gives alternate forms of arachnida or araneidan curves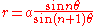
A similar derivation to that above gives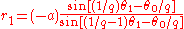
as the polar equation (in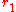 and
and 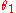 ) if the origin is shifted to the right by
) if the origin is shifted to the right by  . Note that this is the earlier equation with a change of parameters; this to be expected from the fact that two poles are interchangeable in the construction of the curve.
. Note that this is the earlier equation with a change of parameters; this to be expected from the fact that two poles are interchangeable in the construction of the curve.
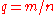 where
where  and
and  are integers and the fraction is in lowest terms. In the notation of the previous section, we have
are integers and the fraction is in lowest terms. In the notation of the previous section, we have
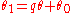 or
or
 .
.
If then
then 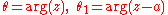 , so the equation becomes
, so the equation becomes
 or
or
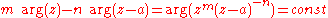 . This can also be written
. This can also be written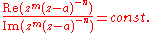
from which it is relatively simple to derive the Cartesian equation given m and n. The function
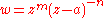 is analytic so the orthoganal trajectories of the family
is analytic so the orthoganal trajectories of the family 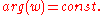 are the curves
are the curves 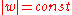 , or
, or
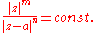
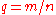 where
where  and
and  are integers, and let
are integers, and let  where
where 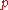 is a parameter. Then converting the polar equation above to parametric equations produces
is a parameter. Then converting the polar equation above to parametric equations produces
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin
Trisectrix of Maclaurin
In geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...
(named for Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
), which is a prominent member of the family, and their sectrix
Trisectrix
In geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...
property, which means they can be used to divide an angle into a given number of equal parts. There are special cases are also known as arachnida or araneidans because of their spider
Spider
Spiders are air-breathing arthropods that have eight legs, and chelicerae with fangs that inject venom. They are the largest order of arachnids and rank seventh in total species diversity among all other groups of organisms...
-like shape, and Plateau curves after Joseph Plateau who studied them.
Equations in polar coordinates
We are given two lines rotating about two poles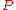 and
and 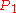 . By translation and rotation we may assume
. By translation and rotation we may assume 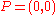 and
and 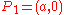 . At time
. At time  , the line rotating about
, the line rotating about 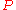 has angle
has angle 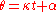 and the line rotating about
and the line rotating about 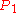 has angle
has angle 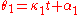 , where
, where  ,
,  ,
, 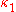 and
and 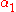 are constants. Eliminate
are constants. Eliminate  to get
to get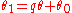 where
where 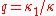 and
and 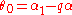 . We assume
. We assume 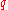 is rational, otherwise the curve is not algebraic and is dense in the plane. Let
is rational, otherwise the curve is not algebraic and is dense in the plane. Let  be the point of intersection of the two lines and let
be the point of intersection of the two lines and let 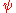 be the angle at
be the angle at  , so
, so 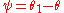 . If
. If  is the distance from
is the distance from 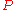 to
to  then, by the law of sines
then, by the law of sinesLaw of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
,
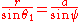
so
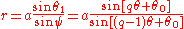
is the equation in polar coordinates.
The case
 and
and  where
where  is an integer greater than 2 gives arachnida or araneidan curves
is an integer greater than 2 gives arachnida or araneidan curves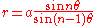
The case
 and
and 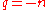 where
where  is an integer greater than 1 gives alternate forms of arachnida or araneidan curves
is an integer greater than 1 gives alternate forms of arachnida or araneidan curves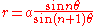
A similar derivation to that above gives
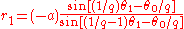
as the polar equation (in
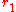 and
and 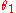 ) if the origin is shifted to the right by
) if the origin is shifted to the right by  . Note that this is the earlier equation with a change of parameters; this to be expected from the fact that two poles are interchangeable in the construction of the curve.
. Note that this is the earlier equation with a change of parameters; this to be expected from the fact that two poles are interchangeable in the construction of the curve.Equations in the complex plane, rectangular coordinates and orthogonal trajectories
Let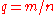 where
where  and
and  are integers and the fraction is in lowest terms. In the notation of the previous section, we have
are integers and the fraction is in lowest terms. In the notation of the previous section, we have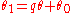 or
or .
.If
 then
then 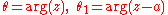 , so the equation becomes
, so the equation becomes or
or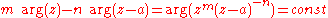 . This can also be written
. This can also be written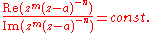
from which it is relatively simple to derive the Cartesian equation given m and n. The function
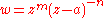 is analytic so the orthoganal trajectories of the family
is analytic so the orthoganal trajectories of the family 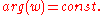 are the curves
are the curves 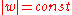 , or
, or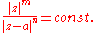
Parametric equations
Let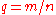 where
where  and
and  are integers, and let
are integers, and let  where
where 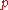 is a parameter. Then converting the polar equation above to parametric equations produces
is a parameter. Then converting the polar equation above to parametric equations produces
-
 .
.
Applying the angle addition rule for sine produces-
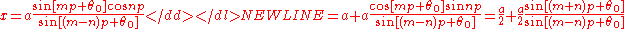 .
.
So if the origin is shifted to the right by a/2 then the parametric equations are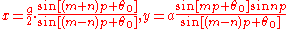 .
.
These are the equations for Plateau curves when , or
, or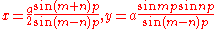 .
.
Inversive triplets
The inverseInverse curveIn geometry, an inverse curve of a given curve C is the result of applying an inverse operation to C. Specifically, with respect to a fixed circle with center O and radius k the inverse of a point Q is the point P for which P lies on the ray OQ and OP·PQ = k2...
with respect to the circle with radius a and center at the origin of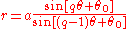
is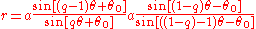 .
.
This is another curve in the family. The inverse with respect to the other pole produces yet another curve in the same family and the two inverses are in turn inverses of each other. Therefore each curve in the family is a member of a triple, each of which belongs to the family and is an inverse of the other two. The values of q in this family are .
.
Sectrix properties
Let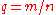 where
where  and
and  are integers in lowest terms and assume
are integers in lowest terms and assume  is constructible with compass and straightedge. (The value of
is constructible with compass and straightedge. (The value of  is usually 0 in practice so this is not normally an issue.) Let
is usually 0 in practice so this is not normally an issue.) Let 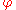 be a given angle and suppose that the sectrix of Maclaurin has been drawn with poles
be a given angle and suppose that the sectrix of Maclaurin has been drawn with poles 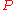 and
and 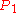 according to the construction above. Construct a ray from
according to the construction above. Construct a ray from 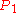 at angle
at angle  and let
and let  be the point of intersection of the ray and the sectrix and draw
be the point of intersection of the ray and the sectrix and draw  . If
. If 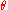 is the angle of this line then
is the angle of this line then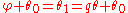
so
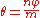 .
.
By repeatedly subtracting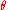 and
and 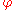 from each other as in the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
from each other as in the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
, the angle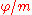 can be constructed. Thus, the curve is an m-sectrix, meaning that with the aid of the curve an arbitrary angle can be divided by any integer. This is a generalization of the concept of a trisectrixTrisectrixIn geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...
can be constructed. Thus, the curve is an m-sectrix, meaning that with the aid of the curve an arbitrary angle can be divided by any integer. This is a generalization of the concept of a trisectrixTrisectrixIn geometry, a trisectrix is a curve which can be used to trisect an arbitrary angle. Such a method falls outside those allowed by compass and straightedge constructions, so they do not contradict the well known theorem which states that an arbitrary angle cannot be trisected with that type of...
and examples of these will be found below.
Now draw a ray with angle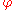 from
from 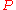 and
and  be the point of intersection of this ray with the curve. The angle of
be the point of intersection of this ray with the curve. The angle of 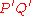 is
is
and subtracting gives an angle of
gives an angle of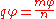 .
.
Applying the Euclidean Algorithm again gives an angle of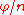 showing that the curve is also an n-sectrix.
showing that the curve is also an n-sectrix.
Finally, draw a ray from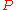 with angle
with angle 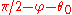 and a ray from
and a ray from 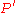 with angle
with angle 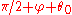 , and let
, and let  be the point of intersection. This point is on the perpendicular bisector of
be the point of intersection. This point is on the perpendicular bisector of 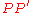 so there is a circle with center
so there is a circle with center  containing
containing 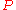 and
and 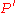 .
. 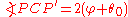 so any point on the circle forms an angle of
so any point on the circle forms an angle of  between
between 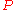 and
and 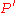 . (This is, in fact, one of the Apollonian circlesApollonian circlesApollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
. (This is, in fact, one of the Apollonian circlesApollonian circlesApollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
of P and P.) Let be the point intersection of this circle and the curve. Then
be the point intersection of this circle and the curve. Then
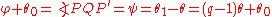
so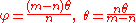 .
.
Applying a Euclidean algorithm a third time gives an angle of , showing that the curve is an (m−n)-sectrix as well.
, showing that the curve is an (m−n)-sectrix as well.
q = 0
This is the curve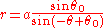
which is line through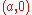
q = 1
This is a circle containing the origin and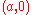 . It has polar equation
. It has polar equation .
.
It is the inverse with respect to the origin of the q = 0 case. The orthogonal trajectories of the family of circles is the family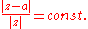 These form the Apollonian circlesApollonian circlesApollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
These form the Apollonian circlesApollonian circlesApollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
with poles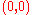 and
and 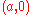 .
.
q = -1
These curves have polar equation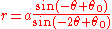 ,
,
complex equation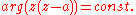 In rectangular coordinates this becomes
In rectangular coordinates this becomes
 which is a conic. From the polar equation it is evident that the curves has asymptotes at
which is a conic. From the polar equation it is evident that the curves has asymptotes at 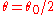 and
and  which are at right angles. So the conics are, in fact, rectangular hyperbolas. The center of the hyperbola is always
which are at right angles. So the conics are, in fact, rectangular hyperbolas. The center of the hyperbola is always 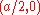 . The orthogonal trajectories of this family are given by
. The orthogonal trajectories of this family are given by
 which is the family of Cassini ovalCassini ovalA Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
which is the family of Cassini ovalCassini ovalA Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
s with foci
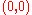 and
and 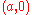 .
.
Trisectrix of Maclaurin
In the case where (or
(or 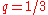 by switching the poles) and
by switching the poles) and  , the equation is
, the equation is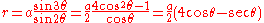 .
.
This is the Trisectrix of MaclaurinTrisectrix of MaclaurinIn geometry, the trisectrix of Maclaurin is a cubic plane curve notable for its trisectrix property, meaning it can be used to trisect an angle. It can be defined as locus of the points of intersection of two lines, each rotating at a uniform rate about separate points, so that the ratio of the...
which is specific case whose generalization is the sectrix of Maclaurin. The construction above gives a method that this curve may be used as a trisectrix.
Limaçon trisectrix
In the case where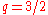 (or
(or 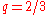 by switching the poles) and
by switching the poles) and  , the equation is
, the equation is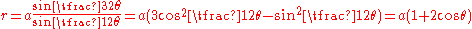 .
.
This is the Limaçon trisectrixLimaçon trisectrixIn geometry, a limaçon trisectrix is a member of the Limaçon family of curves which has the trisectrix, or angle trisection, property...
. The equation with the origin take to be the other pole is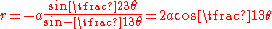 .
.
The 3 in the numerator of q and the construction above give a method that the curve may be used as a trisectrix.
-

