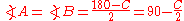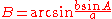
Law of sines
Encyclopedia
In trigonometry
, the law of sines (also known as the sine law, sine formula, or sine rule) is an equation
relating the length
s of the sides of an arbitrary triangle
to the sine
s of its angles. According to the law,

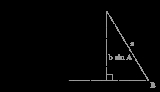
where a, b, and c are the lengths of the sides of a triangle, and A, B, and C are the opposite angles (see the figure to the right). Sometimes the law is stated using the reciprocal
of this equation:
The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation
. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the formula gives two possible values for the enclosed angle, leading to an ambiguous case.
The law of sines is one of two trigonometric equations commonly applied to find lengths and angles in a general triangle, the other being the law of cosines
.
Given: side a = 20, side c = 24, and angle C = 40°
Using the law of sines, we conclude that
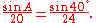

Or another example of how to solve a problem using the law of sines:
If two sides of the triangle are equal to R and the length of the third side, the chord
, is given as 100 feet and the angle C opposite the chord is given in degrees, then
and



Given a general triangle ABC, the following conditions would need to be fulfilled for the case to be ambiguous:
Given all of the above premises are true, the angle B may be acute or obtuse; meaning, one of the following is true:
or

the common value of the three fractions is actually the diameter
of the triangle's circumcircle. It can be shown that this quantity is equal to

where S is the area of the triangle and s is the semiperimeter
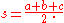
The second equality above is essentially Heron's formula.

Here, α, β, and γ are the angles at the center of the sphere subtended by the three arcs of the spherical surface triangle a, b, and c, respectively. A, B, and C are the surface angles opposite their respective arcs.
when the curvature is −1, the law of sines becomes
In the special case when B is a right angle, one gets
which is the analog of the formula in Euclidean geometry expressing the sine of an angle as the opposite side divided by the hypotenuse.
 :
:
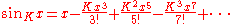
The law of sines in constant curvature reads as
reads as
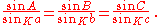
By substituing ,
,  , and
, and  , one obtains respectively the euclidian, spherical, and hyperbolic cases of the law of sines described above.
, one obtains respectively the euclidian, spherical, and hyperbolic cases of the law of sines described above.
Let indicate the circumference of a circle of radius
indicate the circumference of a circle of radius  in a space of constant curvature
in a space of constant curvature  . Then
. Then 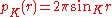 . Therefore the law of sines can also be expressed as:
. Therefore the law of sines can also be expressed as:
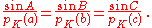
This formulation was discovered by Janos Bolyai
.
and Abu Nasr Mansur
.
Al-Jayyani
's The book of unknown arcs of a sphere in the 11th century introduced the general law of sines. The plane law of sines was later described in the 13th century by Nasīr al-Dīn al-Tūsī
. In his On the Sector Figure, he stated the law of sines for plane and spherical triangles, and provided proofs for this law.
It can be observed that:
Therefore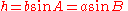
and
Doing the same thing with the line drawn between vertex A and side a will yield:
 of the triangle can be written as any of
of the triangle can be written as any of
Multiplying these by gives
gives
 A corollary of the law of sines as stated above is that in a tetrahedron
A corollary of the law of sines as stated above is that in a tetrahedron
with vertices O, A, B, C, we have
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, the law of sines (also known as the sine law, sine formula, or sine rule) is an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
relating the length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
s of the sides of an arbitrary triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
to the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
s of its angles. According to the law,

where a, b, and c are the lengths of the sides of a triangle, and A, B, and C are the opposite angles (see the figure to the right). Sometimes the law is stated using the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of this equation:
The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation
Triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the formula gives two possible values for the enclosed angle, leading to an ambiguous case.
The law of sines is one of two trigonometric equations commonly applied to find lengths and angles in a general triangle, the other being the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
.
Examples
The following are examples of how to solve a problem using the law of sines:Given: side a = 20, side c = 24, and angle C = 40°
Using the law of sines, we conclude that
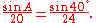

Or another example of how to solve a problem using the law of sines:
If two sides of the triangle are equal to R and the length of the third side, the chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
, is given as 100 feet and the angle C opposite the chord is given in degrees, then
and


Numeric problems
Like the law of cosines, although the law of sines is mathematically true, it has problems for numeric use. Much precision may be lost if an arcsine is computed when the sine of an angle is close to one.Some applications
- The sine law can be used to prove the angle sum identity for sine when α and β are each between 0 and 90 degrees.
- To prove this, make an arbitrary triangle with sides a, b, and c with corresponding arbitrary angles A, B and C. Draw a perpendicular to c from angle C. This will split the angle C into two different angles, α and β, that are less than 90 degrees, where we choose to have α to be on the same side as A and β be on the same side as B. Use the sine law identity that relates side c and side a. Solve this equation for the sine of C. Notice that the perpendicular makes two right angles triangles, also note that sin(A) = cos(α), sin(B) = cos(β) and that c = a sin(β) + b sin(α). After making these substitutions you should have sin(C) =sin(α + β) = sin(β)cos(α) + (b/a)sin(α)cos(α). Now apply the sine law identity that relates sides b and a and make the substitutions noted before. Now substitute this expression for (b/a) into the original equation for sin(α + β) and you will have the angle sum identity for α and β in terms of sine.
- The only thing that was used in the proof that was not a definition was the sine law. Thus the sine law is equivalent to the angle sum identity when the angles sum is between 0 and 180 degrees and when each individual angle is between 0 and 90 degrees.
- The sine law along with the prosthaphaeresisProsthaphaeresisProsthaphaeresis was an algorithm used in the late 16th century and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm in 1614, it was the only known generally-applicable way of approximating...
and shift identities can be used to prove the law of tangentsLaw of tangentsIn trigonometry, the law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposite sides....
and Mollweide's formulas (Dresdin 2009, Plane Trigonometry pg. 76–78 ).
The ambiguous case
When using the law of sines to solve triangles, there exists an ambiguous case where two separate triangles can be constructed (i.e., there are two different possible solutions to the triangle).
Given a general triangle ABC, the following conditions would need to be fulfilled for the case to be ambiguous:
- The only information known about the triangle is the angle A and the sides a and b
- The angle A is acute (i.e., A < 90°).
- The side a is shorter than the side b (i.e., a < b).
- The side a is longer than the altitude of a right angled triangle with angle A and hypotenuse b (i.e., a > b sin A).
Given all of the above premises are true, the angle B may be acute or obtuse; meaning, one of the following is true:
or
Relation to the circumcircle
In the identity
the common value of the three fractions is actually the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the triangle's circumcircle. It can be shown that this quantity is equal to

where S is the area of the triangle and s is the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
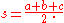
The second equality above is essentially Heron's formula.
Spherical case
In the spherical case, the formula is:
Here, α, β, and γ are the angles at the center of the sphere subtended by the three arcs of the spherical surface triangle a, b, and c, respectively. A, B, and C are the surface angles opposite their respective arcs.
- See also Spherical law of cosines and Half-side formulaHalf-side formulaIn spherical trigonometry, the half side formula relates the angles and lengths of the sides of spherical triangles, which are triangles drawn on the surface of a sphere and so have curved sides and do not obey the formulas for plane triangles....
.
Hyperbolic case
In hyperbolic geometryHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
when the curvature is −1, the law of sines becomes

In the special case when B is a right angle, one gets

which is the analog of the formula in Euclidean geometry expressing the sine of an angle as the opposite side divided by the hypotenuse.
- See also hyperbolic triangleHyperbolic triangleIn mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
.
Unified formulation
Define a generalized sine function, depending also on a real parameter :
: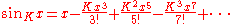
The law of sines in constant curvature
 reads as
reads as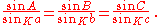
By substituing
 ,
,  , and
, and  , one obtains respectively the euclidian, spherical, and hyperbolic cases of the law of sines described above.
, one obtains respectively the euclidian, spherical, and hyperbolic cases of the law of sines described above.Let
 indicate the circumference of a circle of radius
indicate the circumference of a circle of radius  in a space of constant curvature
in a space of constant curvature  . Then
. Then 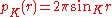 . Therefore the law of sines can also be expressed as:
. Therefore the law of sines can also be expressed as: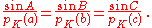
This formulation was discovered by Janos Bolyai
János Bolyai
János Bolyai was a Hungarian mathematician, known for his work in non-Euclidean geometry.Bolyai was born in the Transylvanian town of Kolozsvár , then part of the Habsburg Empire , the son of Zsuzsanna Benkő and the well-known mathematician Farkas Bolyai.-Life:By the age of 13, he had mastered...
.
History
The spherical law of sines was discovered in the 10th century. It is variously attributed to al-Khujandi, Abul Wafa Bozjani, Nasir al-Din al-TusiNasir al-Din al-Tusi
Khawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
and Abu Nasr Mansur
Abu Nasr Mansur
Abu Nasr Mansur ibn Ali ibn Iraq was a Persian Muslim mathematician. He is well known for his work with the spherical sine law....
.
Al-Jayyani
Al-Jayyani
Abū ʿAbd Allāh Muḥammad ibn Muʿādh al-Jayyānī was a mathematician, Islamic scholar, and Qadi from Al-Andalus...
's The book of unknown arcs of a sphere in the 11th century introduced the general law of sines. The plane law of sines was later described in the 13th century by Nasīr al-Dīn al-Tūsī
Nasir al-Din al-Tusi
Khawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
. In his On the Sector Figure, he stated the law of sines for plane and spherical triangles, and provided proofs for this law.
Derivation
Make a triangle with the sides a, b, and c, and angles A, B, and C. Draw the altitude from vertex C to the side across c; by definition it divides the original triangle into two right angle triangles. Mark the length of this line h.It can be observed that:

Therefore
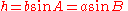
and

Doing the same thing with the line drawn between vertex A and side a will yield:

Alternative derivation
Observe that the area of the triangle can be written as any of
of the triangle can be written as any of
Multiplying these by
 gives
gives
A law of sines for tetrahedra

Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
with vertices O, A, B, C, we have
-

One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface.
Putting any of the four vertices in the role of O yields four such identities, but in a sense at most three of them are independent: If the "clockwise" sides of three of them are multiplied and the product is inferred to be equal to the product of the "counterclockwise" sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity. One reason to be interested in this "independence" relation is this: It is widely known that three angles are the angles of some triangle if and only if their sum is a half-circle. What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be a half-circle. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
is thereby reduced from 12 to 8. The four relations given by this sines law further reduce the number of degrees of freedom, not from 8 down to 4, but only from 8 down to 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional.
See also
- Law of cosinesLaw of cosinesIn trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
- Law of tangentsLaw of tangentsIn trigonometry, the law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposite sides....
- Mollweide's formulaMollweide's formulaIn trigonometry, Mollweide's formula, sometimes referred to in older texts as Mollweide's equations, named after Karl Mollweide, is a set of two relationships between sides and angles in a triangle...
– for checking solutions of triangles - Half-side formulaHalf-side formulaIn spherical trigonometry, the half side formula relates the angles and lengths of the sides of spherical triangles, which are triangles drawn on the surface of a sphere and so have curved sides and do not obey the formulas for plane triangles....
– for solving spherical triangles - SurveyingSurveyingSee Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
- GersonidesGersonidesLevi ben Gershon, better known by his Latinised name as Gersonides or the abbreviation of first letters as RaLBaG , philosopher, Talmudist, mathematician, astronomer/astrologer. He was born at Bagnols in Languedoc, France...
External links
- The Law of Sines at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Degree of Curvature
- Finding the Sine of 1 Degree
- Law of cosines