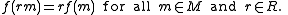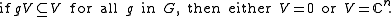Schur's lemma
Encyclopedia
In mathematics
, Schur's lemma is an elementary but extremely useful statement in representation theory
of groups
and algebra
s. In the group case it says that if M and N are two finite-dimensional irreducible representations
of a group G and φ is a linear map from M to N that commutes with the action of the group, then either φ is invertible, or φ = 0. An important special case occurs when M = N and φ is a self-map. The lemma is named after Issai Schur
who used it to prove Schur orthogonality relations
and develop the basics of the representation theory of finite groups
. Schur's lemma admits generalisations to Lie group
s and Lie algebra
s, the most common of which is due to Jacques Dixmier
.
s over a ring R, then any homomorphism
f: M → N of R-modules is either invertible or zero. In particular, the endomorphism ring
of a simple module is a division ring
.
The condition that f is a module homomorphism means that
The group version is a special case of the module version, since any representation of a group G can equivalently be viewed as a module over the group ring
of G.
Schur's lemma is frequently applied in the following particular case. Suppose that R is an algebra
over the field C of complex numbers and M = N is a finite-dimensional simple module over R. Then Schur's lemma says that the endomorphism ring of the module M is a division ring; this division ring contains C in its center, is finite-dimensional over C and is therefore equal to C. Thus the endomorphism ring
of the module M is "as small as possible". More generally, this result holds for algebras over any algebraically closed field and for simple modules that are at most countably-dimensional. When the field is not algebraically closed, the case where the endomorphism ring is as small as possible is of particular interest: A simple module over k-algebra is said to be absolutely simple
if its endomorphism ring is isomorphic to k. This is in general stronger than being irreducible over the field k, and implies the module is irreducible even over the algebraic closure of k.
. This means that G is a set of square matrices of a given order n with complex entries and G is closed under matrix multiplication
and inversion. Further, suppose that G is irreducible: there is no subspace
V other than 0 and the whole space which is invariant under the action of G. In other words,
Schur's lemma, in the special case of a single representation, says the following. If A is a complex matrix of order n that commute
s with all matrices from G then A is a scalar matrix. As a simple corollary, every complex irreducible representation of Abelian group
s is one-dimensional.
See also Schur complement
.
of M.
A module is said to be strongly indecomposable if its endomorphism ring is a local ring
. For the important class of modules of finite length
, the following properties are equivalent :
In general, Schur's lemma cannot be reversed: there exist modules that are not simple, yet their endomorphism algebra is a division ring
. Such modules are necessarily indecomposable, and so cannot exist over semi-simple rings such as the complex group ring of a finite group. However, even over the ring of integer
s, the module of rational number
s has an endomorphism ring that is a division ring, specifically the field of rational numbers. Even for group rings, there are examples when the characteristic of the field divides the order of the group: the Jacobson radical
of the projective cover
of the one-dimensional representation of the alternating group on five points over the field with three elements has the field with three elements as its endomorphism ring.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Schur's lemma is an elementary but extremely useful statement in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
s. In the group case it says that if M and N are two finite-dimensional irreducible representations
of a group G and φ is a linear map from M to N that commutes with the action of the group, then either φ is invertible, or φ = 0. An important special case occurs when M = N and φ is a self-map. The lemma is named after Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
who used it to prove Schur orthogonality relations
Schur orthogonality relations
In mathematics, the Schur orthogonality relations express a central fact about representations of finite groups.They admit a generalization to the case of compact groups in general, and in particular compact Lie groups, such as therotation group SO....
and develop the basics of the representation theory of finite groups
Representation theory of finite groups
In mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
. Schur's lemma admits generalisations to Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, the most common of which is due to Jacques Dixmier
Jacques Dixmier
Jacques Dixmier is a French mathematician. He worked on operator algebras, and wrote several of the standard reference books on them, and introduced the Dixmier trace. He received his Ph.D. in 1949 from the University of Paris, and his students include Alain Connes.-Publications:*J. Dixmier,...
.
Formulation in the language of modules
If M and N are two simple moduleSimple module
In mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
s over a ring R, then any homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
f: M → N of R-modules is either invertible or zero. In particular, the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of a simple module is a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
.
The condition that f is a module homomorphism means that
The group version is a special case of the module version, since any representation of a group G can equivalently be viewed as a module over the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of G.
Schur's lemma is frequently applied in the following particular case. Suppose that R is an algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
over the field C of complex numbers and M = N is a finite-dimensional simple module over R. Then Schur's lemma says that the endomorphism ring of the module M is a division ring; this division ring contains C in its center, is finite-dimensional over C and is therefore equal to C. Thus the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of the module M is "as small as possible". More generally, this result holds for algebras over any algebraically closed field and for simple modules that are at most countably-dimensional. When the field is not algebraically closed, the case where the endomorphism ring is as small as possible is of particular interest: A simple module over k-algebra is said to be absolutely simple
Absolutely irreducible
In mathematics, absolutely irreducible is a term applied to linear representations or algebraic varieties over a field. It means that the object in question remains irreducible, even after any finite extension of the field of coefficients...
if its endomorphism ring is isomorphic to k. This is in general stronger than being irreducible over the field k, and implies the module is irreducible even over the algebraic closure of k.
Matrix form
Let G be a complex matrix groupMatrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
. This means that G is a set of square matrices of a given order n with complex entries and G is closed under matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and inversion. Further, suppose that G is irreducible: there is no subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
V other than 0 and the whole space which is invariant under the action of G. In other words,
Schur's lemma, in the special case of a single representation, says the following. If A is a complex matrix of order n that commute
Commute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
s with all matrices from G then A is a scalar matrix. As a simple corollary, every complex irreducible representation of Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s is one-dimensional.
See also Schur complement
Schur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
.
Generalization to non-simple modules
The one module version of Schur's lemma admits generalizations involving modules M that are not necessarily simple. They express relations between the module-theoretic properties of M and the properties of the endomorphism ringEndomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of M.
A module is said to be strongly indecomposable if its endomorphism ring is a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
. For the important class of modules of finite length
Length of a module
In abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
, the following properties are equivalent :
- A module M is indecomposableIndecomposable moduleIn abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
; - M is strongly indecomposable;
- Every endomorphism of M is either nilpotent or invertible.
In general, Schur's lemma cannot be reversed: there exist modules that are not simple, yet their endomorphism algebra is a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
. Such modules are necessarily indecomposable, and so cannot exist over semi-simple rings such as the complex group ring of a finite group. However, even over the ring of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, the module of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s has an endomorphism ring that is a division ring, specifically the field of rational numbers. Even for group rings, there are examples when the characteristic of the field divides the order of the group: the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of the projective cover
Projective cover
In the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.- Definition :...
of the one-dimensional representation of the alternating group on five points over the field with three elements has the field with three elements as its endomorphism ring.