
Schneider–Lang theorem
Encyclopedia
In mathematics, the Schneider–Lang theorem is a refinement by of a theorem of about the transcendence
of values of meromorphic function
s. The theorem implies both the Hermite–Lindemann and Gelfond–Schneider theorems, and implies the transcendence of some values of elliptic function
s and elliptic modular functions.
s ρ1 and ρ2, and such that if we differentiate any of these functions then the result is a polynomial in all of the functions. Under these hypotheses the theorem states that if there are m distinct complex number
s ω1, ..., ωm such that fi (ωj ) is in K for all combinations of i and j, then m is bounded by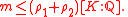
Lang showed how to make F in such a way that it vanished to a high order at the m complex numbers
ω1,...,ωm. Because of this high order vanishing it can be shown that a high-order derivative of F takes a value of small size one of the ωis, "size" here referring to an algebraic property of a number. Using the maximum modulus principle
Lang also found a separate way to estimate the absolute values of derivatives of F, and using standard results comparing the size of a number and its absolute value he showed that these estimates were contradicted unless the claimed bound on m holds.
gave a simpler proof of Bombieri's theorem, with a slightly stronger bound of d(ρ1+...+ρd+1)[K:Q] for the degree, where the ρj are the orders of d+1 algebraically independent functions.
The special case d = 1 gives the Schneider–Lang theorem, with a bound of (ρ1+ρ2)[K:Q] for the number of points.
Example. If p is a polynomial with integer coefficients then the functions z1,...,zn,ep(z1,...,zn) are all algebraic at a dense set of points of the hypersurface p=0.
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
of values of meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s. The theorem implies both the Hermite–Lindemann and Gelfond–Schneider theorems, and implies the transcendence of some values of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s and elliptic modular functions.
Statement
The theorem deals with a number field K and meromorphic functions f1, ..., fN, at least two of which are algebraically independent of orderEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s ρ1 and ρ2, and such that if we differentiate any of these functions then the result is a polynomial in all of the functions. Under these hypotheses the theorem states that if there are m distinct complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s ω1, ..., ωm such that fi (ωj ) is in K for all combinations of i and j, then m is bounded by
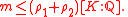
Examples
- If the two functions are f1 = z and f1 = ez then the theorem implies the Hermite–Lindemann theorem that eα is transcendental for any nonzero algebraic α, otherwise α, 2α, 3α,... would be an infinite number of values at which both f1 and f2 are algebraic.
- Similarly taking the two function to be f1 = ez and f1 = eβz for β irrational algebraic implies the Gelfond–Schneider theorem that αβ cannot be algebraic if α is algebraic and not 0 or 1. Otherwise log α, 2 log α, 3 log α would be an infinite number of values at which both f1 and f2 are algebraic.
- Taking the three functions to be z, ℘(αz), ℘'(αz) shows that if g2 and g3 are algebraic then the Weierstrass P function ℘(α), which satisfies the differential equation
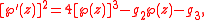
- is transcendental for any algebraic α.
- Taking the functions to be z and ef(z) for a polynomial f of degree ρ shows that the number of points where the functions are all algebraic can grow linearly with the order ρ = deg(f).
Proof
To prove the result Lang took two algebraically independent functions from f1, ..., fN, say f and g, and then created an auxiliary function which was simply a polynomial F in f and g. This auxiliary function could not be explicitly stated since f and g are not explicitly known. But using Siegel's lemmaSiegel's lemma
In transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used Dirichlet's box principle. Carl...
Lang showed how to make F in such a way that it vanished to a high order at the m complex numbers
ω1,...,ωm. Because of this high order vanishing it can be shown that a high-order derivative of F takes a value of small size one of the ωis, "size" here referring to an algebraic property of a number. Using the maximum modulus principle
Maximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
Lang also found a separate way to estimate the absolute values of derivatives of F, and using standard results comparing the size of a number and its absolute value he showed that these estimates were contradicted unless the claimed bound on m holds.
Bombieri's theorem
and generalized the result to functions of several variables. Bombieri showed that if K is an algebraic number field and f1, ..., fN are meromorphic functions of d complex variables of order at most ρ generating a field K( f1, ..., fN) of transcendence degree at least d + 1 that is closed under all partial derivatives, then the set of points where all the functions fn have values in K is contained in an algebraic hypersurface in Cd of degree at most d(d + 1)ρ[K:Q] + dgave a simpler proof of Bombieri's theorem, with a slightly stronger bound of d(ρ1+...+ρd+1)[K:Q] for the degree, where the ρj are the orders of d+1 algebraically independent functions.
The special case d = 1 gives the Schneider–Lang theorem, with a bound of (ρ1+ρ2)[K:Q] for the number of points.
Example. If p is a polynomial with integer coefficients then the functions z1,...,zn,ep(z1,...,zn) are all algebraic at a dense set of points of the hypersurface p=0.

