
Satellite knot
Encyclopedia
In the mathematical theory of knots
, a satellite knot is a knot
that contains an incompressible
, non-boundary parallel
torus
in its complement
. The class of satellite knots include composite
knots, cable knots and Whitehead doubles. (See Basic families, below for definitions of the last two classes.)
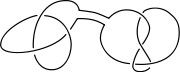 A satellite knot
A satellite knot  can be picturesquely described as follows: start by taking a nontrivial knot
can be picturesquely described as follows: start by taking a nontrivial knot 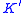 lying inside an unknotted solid torus
lying inside an unknotted solid torus  . Here "nontrivial" means that the knot
. Here "nontrivial" means that the knot 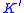 is not allowed to sit inside of a 3-ball in
is not allowed to sit inside of a 3-ball in  and
and 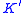 is not allowed to be isotopic to the central core curve of the solid torus. Then tie up the solid torus into a nontrivial knot.
is not allowed to be isotopic to the central core curve of the solid torus. Then tie up the solid torus into a nontrivial knot.  This means there is a non-trivial embedding
This means there is a non-trivial embedding 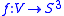 and
and 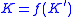 . The central core curve of the solid torus
. The central core curve of the solid torus  is sent to a knot
is sent to a knot  , which is called the "companion knot" and is thought of as the planet around which the "satellite knot"
, which is called the "companion knot" and is thought of as the planet around which the "satellite knot"  orbits.The construction ensures that
orbits.The construction ensures that  is a non-boundary parallel incompressible torus in the complement of
is a non-boundary parallel incompressible torus in the complement of  . Composite knots contain a certain kind of incompressible torus called a swallow-follow torus, which can be visualized as swallowing one summand and following another summand.
. Composite knots contain a certain kind of incompressible torus called a swallow-follow torus, which can be visualized as swallowing one summand and following another summand. 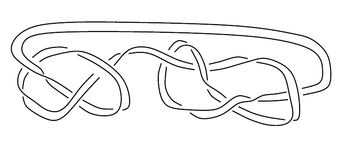 Since
Since  is an unknotted solid torus,
is an unknotted solid torus,  is a tubular neighbourhood of an unknot
is a tubular neighbourhood of an unknot  . The 2-component link
. The 2-component link 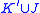 together with the embedding
together with the embedding  is called the pattern associated to the satellite operation.
is called the pattern associated to the satellite operation.
A convention: people usually demand that the embedding is untwisted in the sense that
is untwisted in the sense that 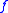 must send the standard longitude of
must send the standard longitude of  to the standard longitude of
to the standard longitude of 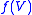 . Said another way, given two disjoint curves
. Said another way, given two disjoint curves 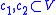 ,
,  must preserve their linking numbers i.e.:
must preserve their linking numbers i.e.:  .
.
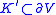 is a torus knot
is a torus knot
, then is called a cable knot. Examples 3 and 4 are cable knots.
is called a cable knot. Examples 3 and 4 are cable knots.
If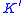 is a non-trivial knot in
is a non-trivial knot in 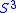 and if a compressing disc for
and if a compressing disc for  intersects
intersects 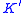 in precisely one point, then
in precisely one point, then  is called a connect-sum. Another way to say this is that the pattern
is called a connect-sum. Another way to say this is that the pattern 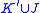 is the connect-sum of a non-trivial knot
is the connect-sum of a non-trivial knot  with a Hopf link.
with a Hopf link.
If the link is the Whitehead link
is the Whitehead link
, is called a Whitehead double. If
is called a Whitehead double. If 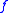 is untwisted,
is untwisted,  is called an untwisted Whitehead double.
is called an untwisted Whitehead double.
Example 2: Untwisted Whitehead double of a figure-8.
Example 3: Cable of a connect-sum.
Example 4: Cable of trefoil.
Examples 5 and 6 are variants on the same construction. They both have two non-parallel, non-boundary-parallel incompressible tori in their complements, splitting the complement into the union of three manifolds. In Example 5 those manifolds are: the Borromean rings
complement, trefoil complement and figure-8 complement. In Example 6 the figure-8 complement is replaced by another trefoil complement.
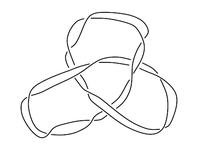
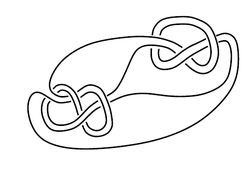
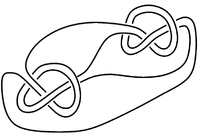
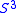 decomposes as a connect-sum of prime knots in a unique way, up to reordering, making the monoid of oriented isotopy-classes of knots in
decomposes as a connect-sum of prime knots in a unique way, up to reordering, making the monoid of oriented isotopy-classes of knots in  a free commutative monoid on countably-infinite many generators. Shortly after, he realized he could give a new proof of his theorem by a close analysis of the incompressible tori present in the complement of a connect-sum. This led him to study general incompressible tori in knot complements in his epic work Knoten und Vollringe, where he defined satellite and companion knots.
a free commutative monoid on countably-infinite many generators. Shortly after, he realized he could give a new proof of his theorem by a close analysis of the incompressible tori present in the complement of a connect-sum. This led him to study general incompressible tori in knot complements in his epic work Knoten und Vollringe, where he defined satellite and companion knots.
of 3-manifolds, which is a decomposition of 3-manifolds along spheres and incompressible tori. This later became a major ingredient in the development of geometrization
, which can be seen as a partial-classification of 3-dimensional manifolds. The ramifications for knot theory were first described in the long-unpublished manuscript of Bonahon and Siebenmann.
gives a proper uniqueness theorem for satellite knots.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a satellite knot is a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
that contains an incompressible
Incompressible surface
In mathematics, an incompressible surface, in intuitive terms, is a surface, embedded in a 3-manifold, which has been simplified as much as possible while remaining "nontrivial" inside the 3-manifold....
, non-boundary parallel
Boundary parallel
In mathematics, a closed n-manifold N embedded in an -manifold M is boundary parallel if there is an isotopy of N onto a boundary component of M.-An example:...
torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
in its complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
. The class of satellite knots include composite
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
knots, cable knots and Whitehead doubles. (See Basic families, below for definitions of the last two classes.)

 can be picturesquely described as follows: start by taking a nontrivial knot
can be picturesquely described as follows: start by taking a nontrivial knot 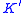 lying inside an unknotted solid torus
lying inside an unknotted solid torus  . Here "nontrivial" means that the knot
. Here "nontrivial" means that the knot 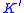 is not allowed to sit inside of a 3-ball in
is not allowed to sit inside of a 3-ball in  and
and 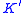 is not allowed to be isotopic to the central core curve of the solid torus. Then tie up the solid torus into a nontrivial knot.
is not allowed to be isotopic to the central core curve of the solid torus. Then tie up the solid torus into a nontrivial knot. 
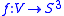 and
and 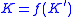 . The central core curve of the solid torus
. The central core curve of the solid torus  is sent to a knot
is sent to a knot  , which is called the "companion knot" and is thought of as the planet around which the "satellite knot"
, which is called the "companion knot" and is thought of as the planet around which the "satellite knot"  orbits.The construction ensures that
orbits.The construction ensures that  is a non-boundary parallel incompressible torus in the complement of
is a non-boundary parallel incompressible torus in the complement of  . Composite knots contain a certain kind of incompressible torus called a swallow-follow torus, which can be visualized as swallowing one summand and following another summand.
. Composite knots contain a certain kind of incompressible torus called a swallow-follow torus, which can be visualized as swallowing one summand and following another summand. 
 is an unknotted solid torus,
is an unknotted solid torus, 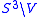 is a tubular neighbourhood of an unknot
is a tubular neighbourhood of an unknot  . The 2-component link
. The 2-component link 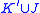 together with the embedding
together with the embedding  is called the pattern associated to the satellite operation.
is called the pattern associated to the satellite operation.A convention: people usually demand that the embedding
 is untwisted in the sense that
is untwisted in the sense that 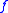 must send the standard longitude of
must send the standard longitude of  to the standard longitude of
to the standard longitude of 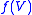 . Said another way, given two disjoint curves
. Said another way, given two disjoint curves 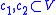 ,
,  must preserve their linking numbers i.e.:
must preserve their linking numbers i.e.:  .
.Basic families
When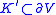 is a torus knot
is a torus knotTorus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
, then
 is called a cable knot. Examples 3 and 4 are cable knots.
is called a cable knot. Examples 3 and 4 are cable knots.If
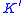 is a non-trivial knot in
is a non-trivial knot in 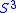 and if a compressing disc for
and if a compressing disc for  intersects
intersects 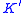 in precisely one point, then
in precisely one point, then  is called a connect-sum. Another way to say this is that the pattern
is called a connect-sum. Another way to say this is that the pattern 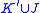 is the connect-sum of a non-trivial knot
is the connect-sum of a non-trivial knot  with a Hopf link.
with a Hopf link.If the link
 is the Whitehead link
is the Whitehead linkWhitehead link
In knot theory, the Whitehead link, discovered by J.H.C. Whitehead, is one of the most basic links.J.H.C. Whitehead spent much of the 1930s looking for a proof of the Poincaré conjecture...
,
 is called a Whitehead double. If
is called a Whitehead double. If 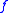 is untwisted,
is untwisted,  is called an untwisted Whitehead double.
is called an untwisted Whitehead double.Examples
Example 1: The connect-sum of a figure-8 knot and trefoil.Example 2: Untwisted Whitehead double of a figure-8.
Example 3: Cable of a connect-sum.
Example 4: Cable of trefoil.
Examples 5 and 6 are variants on the same construction. They both have two non-parallel, non-boundary-parallel incompressible tori in their complements, splitting the complement into the union of three manifolds. In Example 5 those manifolds are: the Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
complement, trefoil complement and figure-8 complement. In Example 6 the figure-8 complement is replaced by another trefoil complement.



Origins
In 1949 Horst Schubert proved that every oriented knot in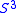 decomposes as a connect-sum of prime knots in a unique way, up to reordering, making the monoid of oriented isotopy-classes of knots in
decomposes as a connect-sum of prime knots in a unique way, up to reordering, making the monoid of oriented isotopy-classes of knots in  a free commutative monoid on countably-infinite many generators. Shortly after, he realized he could give a new proof of his theorem by a close analysis of the incompressible tori present in the complement of a connect-sum. This led him to study general incompressible tori in knot complements in his epic work Knoten und Vollringe, where he defined satellite and companion knots.
a free commutative monoid on countably-infinite many generators. Shortly after, he realized he could give a new proof of his theorem by a close analysis of the incompressible tori present in the complement of a connect-sum. This led him to study general incompressible tori in knot complements in his epic work Knoten und Vollringe, where he defined satellite and companion knots.Follow-up work
Schubert's demonstration that incompressible tori play a major role in knot theory was one several early insights leading to the unification of 3-manifold theory and knot theory. It attracted Waldhausen's attention, who later used incompressible surfaces to show that a large class of 3-manifolds are homeomorphic if and only if their fundamental groups are isomorphic. Waldhausen conjectured what is now the Jaco–Shalen–Johannson-decompositionJSJ decomposition
In mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:The acronym JSJ is for William Jaco, Peter Shalen, and Klaus Johannson...
of 3-manifolds, which is a decomposition of 3-manifolds along spheres and incompressible tori. This later became a major ingredient in the development of geometrization
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
, which can be seen as a partial-classification of 3-dimensional manifolds. The ramifications for knot theory were first described in the long-unpublished manuscript of Bonahon and Siebenmann.
Uniqueness of satellite decomposition
In Knoten und Vollringe, Schubert proved that in some cases, there is essentially a unique way to express a knot as a satellite. But there are also many known examples where the decomposition is not unique. With a suitably enhanced notion of satellite operation called splicing, the JSJ decompositionJSJ decomposition
In mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:The acronym JSJ is for William Jaco, Peter Shalen, and Klaus Johannson...
gives a proper uniqueness theorem for satellite knots.

