Rational mapping
Encyclopedia
In mathematics
, in particular the subfield of algebraic geometry
, a rational map is a kind of partial function
between algebraic varieties. This article uses the convention that varieties are irreducible.
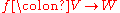between two varieties is an equivalence class of pairs 
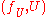in which 
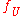is a morphism of varieties from an open set 
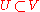to 
, and two such pairs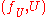 
and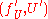 
are considered equivalent if 
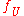and 
coincide on the intersection 
(this is, in particular, vacuously true
if the intersection is empty, but since
is assumed irreducible, this is impossible). The proof that this defines an equivalence relation relies on the following lemma:
is said to be birational if there exists a rational map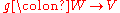 
which is its inverse, where the composition is taken in the above sense.
The importance of rational maps to algebraic geometry is in the connection between such maps and maps between the function field
s of
and 
. Even a cursory examination of the definitions reveals a similarity between that of rational map and that of rational function; in fact, a rational function is just a rational map whose range is the projective line. Composition of functions then allows us to "pull back" rational functions along a rational map, so that a single rational map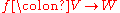 
induces a homomorphism of fields 
. In particular, the following theorem is central: the functor
from the category of projective varieties with dominant rational maps (over a fixed base field, for example
) to the category of field extensions of the base field with reverse inclusion of extensions as morphisms, which associates each variety to its function field and each map to the associated map of function fields, is an equivalence of categories
.
The usual example is that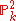
is birational to the variety 
contained in 
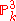consisting of the set of projective points 
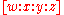such that 
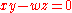, but not isomorphic. Indeed, any two lines in 
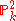intersect, but the lines in 
defined by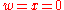 
and 
cannot intersect since their intersection would have all coordinates zero. To compute the function field of 
we pass to an affine subset (which does not change the field, a manifestation of the fact that a rational map depends only on its behavior in any open subset of its domain) in which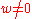 
; in projective space this means we may take 
and therefore identify this subset with the affine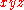 
-plane. There, the coordinate ring of 
is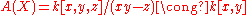
via the map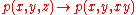
. And the field of fractions
of the latter is just
, isomorphic to that of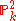 
. Note that at no time did we actually produce a rational map, though tracing through the proof of the theorem it is possible to do so.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular the subfield of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a rational map is a kind of partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
between algebraic varieties. This article uses the convention that varieties are irreducible.
Formal definition
Formally, a rational map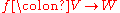 between two varieties is an equivalence class of pairs 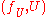in which 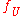is a morphism of varieties from an open set 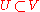to , and two such pairs 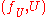and 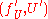are considered equivalent if 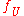and coincide on the intersection (this is, in particular, vacuously trueVacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
if the intersection is empty, but since
is assumed irreducible, this is impossible). The proof that this defines an equivalence relation relies on the following lemma:- If two morphisms of varieties are equal on any open set, then they are equal.
is said to be birational if there exists a rational map 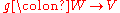which is its inverse, where the composition is taken in the above sense.The importance of rational maps to algebraic geometry is in the connection between such maps and maps between the function field
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
s of
and . Even a cursory examination of the definitions reveals a similarity between that of rational map and that of rational function; in fact, a rational function is just a rational map whose range is the projective line. Composition of functions then allows us to "pull back" rational functions along a rational map, so that a single rational map 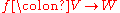induces a homomorphism of fields . In particular, the following theorem is central: the functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of projective varieties with dominant rational maps (over a fixed base field, for example
) to the category of field extensions of the base field with reverse inclusion of extensions as morphisms, which associates each variety to its function field and each map to the associated map of function fields, is an equivalence of categoriesEquivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
.
An example of birational equivalence
Two varieties are said to be birationally equivalent if there exists a birational map between them; this theorem states that birational equivalence of varieties is identical to isomorphism of their function fields as extensions of the base field. This is somewhat more liberal than the notion of isomorphism of varieties (which requires a globally defined morphism to witness the isomorphism, not merely a rational map), in that there exist varieties which are birational but not isomorphic.The usual example is that
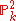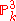is birational to the variety contained in consisting of the set of projective points 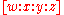such that 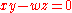, but not isomorphic. Indeed, any two lines in 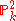intersect, but the lines in defined by 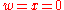and cannot intersect since their intersection would have all coordinates zero. To compute the function field of we pass to an affine subset (which does not change the field, a manifestation of the fact that a rational map depends only on its behavior in any open subset of its domain) in which 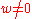; in projective space this means we may take and therefore identify this subset with the affine 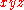-plane. There, the coordinate ring of is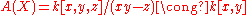via the map
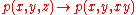. And the field of fractionsField of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the latter is just
, isomorphic to that of 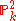. Note that at no time did we actually produce a rational map, though tracing through the proof of the theorem it is possible to do so.