Range criterion
Encyclopedia
In quantum mechanics
, in particular quantum information
, the Range criterion is a necessary condition that a state must satisfy in order to be separable
. In other words, it is a separability criterion.
.
For simplicity we will assume throughout that all relevant state spaces are finite dimensional.
The criterion reads as follows: If ρ is a separable mixed state acting on H, then the range of ρ is spanned by a set of product vectors.
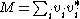, it is obvious that the range of M, Ran(M), is contained in the linear span of 
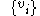. On the other hand, we can also show 
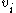lies in Ran(M), for all i. Assume without loss of generality i = 1. We can write
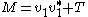, where T is Hermitian and positive semidefinite. There are two possibilities:
1) span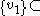
Ker(T). Clearly, in this case, 
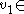Ran(M).
2) Notice 1) is true if and only if Ker(T)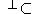
span
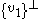, where 
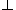denotes orthogonal compliment. By Hermiticity of T, this is the same as Ran(T)
span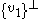
. So if 1) does not hold, the intersection Ran(T) 
span
is nonempty, i.e. there exists some complex number α such that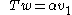 
. So
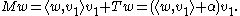
Therefore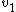
lies in Ran(M).
Thus Ran(M) coincides with the linear span of
. The range criterion is a special case of this fact.
A density matrix ρ acting on H is separable if and only if it can be written as
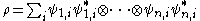
where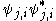
is a (un-normalized) pure state on the j-th subsystem. This is also
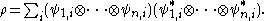
But this is exactly the same form as M from above, with the vectorial product state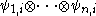
replacing 
. It then immediately follows that the range of ρ is the linear span of these product states. This proves the criterion.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, in particular quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
, the Range criterion is a necessary condition that a state must satisfy in order to be separable
Separable states
In quantum mechanics, separable quantum states are states without quantum entanglement.- Separable pure states :For simplicity, the following assumes all relevant state spaces are finite dimensional...
. In other words, it is a separability criterion.
The result
Consider a quantum mechanical system composed of n subsystems. The state space H of such a system is the tensor product of those of the subsystems, i.e..For simplicity we will assume throughout that all relevant state spaces are finite dimensional.
The criterion reads as follows: If ρ is a separable mixed state acting on H, then the range of ρ is spanned by a set of product vectors.
Proof
In general, if a matrix M is of the form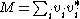, it is obvious that the range of M, Ran(M), is contained in the linear span of 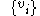. On the other hand, we can also show 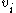lies in Ran(M), for all i. Assume without loss of generality i = 1. We can write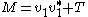, where T is Hermitian and positive semidefinite. There are two possibilities:1) span
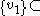Ker(T). Clearly, in this case, 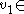Ran(M).2) Notice 1) is true if and only if Ker(T)
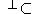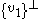span, where 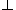denotes orthogonal compliment. By Hermiticity of T, this is the same as Ran(T) span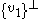. So if 1) does not hold, the intersection Ran(T) span is nonempty, i.e. there exists some complex number α such that 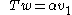. So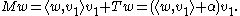Therefore
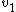lies in Ran(M).Thus Ran(M) coincides with the linear span of
. The range criterion is a special case of this fact.A density matrix ρ acting on H is separable if and only if it can be written as
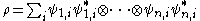
where
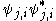is a (un-normalized) pure state on the j-th subsystem. This is also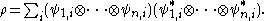But this is exactly the same form as M from above, with the vectorial product state
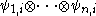replacing . It then immediately follows that the range of ρ is the linear span of these product states. This proves the criterion.