Radon's theorem
Encyclopedia
In geometry
, Radon's theorem on convex set
s, named after Johann Radon
, states that any set of d + 2 points in R
d can be partitioned
into two (disjoint) sets whose convex hull
s intersect. A point in the intersection of these hulls is called a Radon point of the set.
For example, in the case d = 2, any set of four points in the Euclidean plane can be partitioned in one of two ways. It may form a triple and a singleton, where the convex hull of the triple (a triangle) contains the singleton; alternatively, it may form two pairs of points that form the endpoints of two intersecting line segment
s.
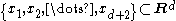of d + 2 points in d-dimensional space. Then there exists a set of multipliers a1, ..., ad + 2, not all of which are zero, solving the system of linear equations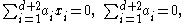
because there are d + 2 unknowns (the multipliers) but only d + 1 equations that they must satisfy (one for each coordinate of the points, together with a final equation requiring the sum of the multipliers to be zero). Fix some particular nonzero solution a1, ..., ad + 2. Let I be the set of points with positive multipliers, and let J be the set of points with multipliers that are negative or zero. Then I and J form the required partition of the points into two subsets with intersecting convex hulls.
The convex hulls of I and J must intersect, because they both contain the point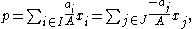
where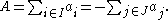
The left hand side of the formula for p expresses this point as a convex combination
of the points in I, and the right hand side expresses it as a convex combination of the points in J. Therefore, p belongs to both convex hulls, completing the proof.
This proof method allows for the efficient construction of a Radon point, in an amount of time that is polynomial in the dimension, by using Gaussian elimination
or other efficient algorithms to solve the system of equations for the multipliers.
generalization of Radon's theorem states that, if ƒ is any continuous function
from a (d + 1)-dimensional simplex
to d-dimensional space, then the simplex has two disjoint faces whose images under ƒ are not disjoint. Radon's theorem itself can be interpreted as the special case in which ƒ is the unique affine map that takes the vertices of the simplex to a given set of d + 2 points in d-dimensional space.
More generally, if K is any (d + 1)-dimensional compact convex set, and ƒ is any continuous function from K to d-dimensional space, then there exists a linear function g such that some point where g achieves its maximum value and some other point where g achieves its minimum value are mapped by ƒ to the same point. In the case where K is a simplex, the two simplex faces formed by the maximum and minimum points of g must then be two disjoint faces whose images have a nonempty intersection. This same general statement, when applied to a hypersphere
instead of a simplex, gives the Borsuk–Ulam theorem
, that ƒ must map two opposite points of the sphere to the same point.
on intersections of convex sets; this proof was the motivation for Radon's original discovery of Radon's theorem.
Radon's theorem can also be used to calculate the VC dimension
of d-dimensional points with respect to linear separations. There exist sets of d + 1 points (for instance, the points of a regular simplex) such that every two nonempty subsets can be separated from each other by a hyperplane. However, no matter which set of d + 2 points is given, the two subsets of a Radon partition cannot be linearly separated. Therefore, the VC dimension of this system is exactly d + 1.
A randomized algorithm
that repeatedly replaces sets of d + 2 points by their Radon point can be used to compute an approximation
to a centerpoint
of any point set, in an amount of time that is polynomial in both the number of points and the dimension.
. The geometric median
of a set of points is the point minimizing the sum of distances to the points in the set; it generalizes the one-dimensional median and has been studied both from the point of view of facility location
and robust statistics
. For sets of four points in the plane, the geometric median coincides with the Radon point.
Another generalization for partition into r sets was given by and is now known as Tverberg's theorem
. It states that for any set of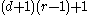
points in Euclidean d-space, there is a partition into r subsets whose convex hulls intersect in at least one common point.
Carathéodory's theorem
states that any point in the convex hull of some set of points is also within the convex hull of a subset of at most d + 1 of the points; that is, that the given point is part of a Radon partition in which it is a singleton. One proof of Carathéodory's theorem uses a technique of examining solutions to systems of linear equations, similar to the proof of Radon's theorem, to eliminate one point at a time until at most d + 1 remain.
Concepts related to Radon's theorem have also been considered for convex geometries
, families of finite sets with the properties that the intersection of any two sets in the family remains in the family, and that the empty set
and the union of all the sets belongs to the family. In this more general context, the convex hull of a set S is the intersection of the family members that contain S, and the Radon number of a space is the smallest r such that any r points have two subsets whose convex hulls intersect. Similarly, one can define the Helly number h and the Carathéodory number c by analogy to their definitions for convex sets in Euclidean spaces, and it can be shown that these numbers satisfy the inequalities h < r ≤ ch + 1.
In an arbitrary undirected graph, one may define a convex set to be a set of vertices that includes every induced path
connecting a pair of vertices in the set. With this definition, every set of ω + 1 vertices in the graph can be partitioned into two subsets whose convex hulls intersect, and ω + 1 is the minimum number for which this is possible, where ω is the clique number of the given graph. For related results involving shortest paths instead of induced paths see and .
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Radon's theorem on convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s, named after Johann Radon
Johann Radon
Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
, states that any set of d + 2 points in R
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
d can be partitioned
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into two (disjoint) sets whose convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
s intersect. A point in the intersection of these hulls is called a Radon point of the set.
For example, in the case d = 2, any set of four points in the Euclidean plane can be partitioned in one of two ways. It may form a triple and a singleton, where the convex hull of the triple (a triangle) contains the singleton; alternatively, it may form two pairs of points that form the endpoints of two intersecting line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s.
Proof and construction
Consider any set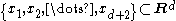 of d + 2 points in d-dimensional space. Then there exists a set of multipliers a1, ..., ad + 2, not all of which are zero, solving the system of linear equations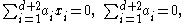because there are d + 2 unknowns (the multipliers) but only d + 1 equations that they must satisfy (one for each coordinate of the points, together with a final equation requiring the sum of the multipliers to be zero). Fix some particular nonzero solution a1, ..., ad + 2. Let I be the set of points with positive multipliers, and let J be the set of points with multipliers that are negative or zero. Then I and J form the required partition of the points into two subsets with intersecting convex hulls.
The convex hulls of I and J must intersect, because they both contain the point
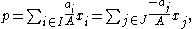
where
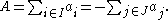
The left hand side of the formula for p expresses this point as a convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of the points in I, and the right hand side expresses it as a convex combination of the points in J. Therefore, p belongs to both convex hulls, completing the proof.
This proof method allows for the efficient construction of a Radon point, in an amount of time that is polynomial in the dimension, by using Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
or other efficient algorithms to solve the system of equations for the multipliers.
Topological Radon theorem
A topologicalTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
generalization of Radon's theorem states that, if ƒ is any continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
from a (d + 1)-dimensional simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
to d-dimensional space, then the simplex has two disjoint faces whose images under ƒ are not disjoint. Radon's theorem itself can be interpreted as the special case in which ƒ is the unique affine map that takes the vertices of the simplex to a given set of d + 2 points in d-dimensional space.
More generally, if K is any (d + 1)-dimensional compact convex set, and ƒ is any continuous function from K to d-dimensional space, then there exists a linear function g such that some point where g achieves its maximum value and some other point where g achieves its minimum value are mapped by ƒ to the same point. In the case where K is a simplex, the two simplex faces formed by the maximum and minimum points of g must then be two disjoint faces whose images have a nonempty intersection. This same general statement, when applied to a hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
instead of a simplex, gives the Borsuk–Ulam theorem
Borsuk–Ulam theorem
In mathematics, the Borsuk–Ulam theorem, named after Stanisław Ulam and Karol Borsuk, states that every continuous function from an n-sphere into Euclidean n-space maps some pair of antipodal points to the same point....
, that ƒ must map two opposite points of the sphere to the same point.
Applications
Radon's theorem forms a key step of a standard proof of Helly's theoremHelly's theorem
Helly's theorem is a basic result in discrete geometry describing the ways that convex sets may intersect each other. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared...
on intersections of convex sets; this proof was the motivation for Radon's original discovery of Radon's theorem.
Radon's theorem can also be used to calculate the VC dimension
VC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
of d-dimensional points with respect to linear separations. There exist sets of d + 1 points (for instance, the points of a regular simplex) such that every two nonempty subsets can be separated from each other by a hyperplane. However, no matter which set of d + 2 points is given, the two subsets of a Radon partition cannot be linearly separated. Therefore, the VC dimension of this system is exactly d + 1.
A randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
that repeatedly replaces sets of d + 2 points by their Radon point can be used to compute an approximation
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
to a centerpoint
Centerpoint
Centerpoint is used in several senses:* Centerpoint , a generalization of the median to two or more dimensions-Organizations:* CenterPoint Energy, an electric and natural gas utility in the US...
of any point set, in an amount of time that is polynomial in both the number of points and the dimension.
Related concepts
The Radon point of three points in a one-dimensional space is just their medianMedian
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
. The geometric median
Geometric median
The geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher...
of a set of points is the point minimizing the sum of distances to the points in the set; it generalizes the one-dimensional median and has been studied both from the point of view of facility location
Facility location
Facility location, also known as location analysis, is a branch of operations research and computational geometry concerning itself with mathematical modeling and solution of problems concerning optimal placement of facilities in order to minimize transportation costs, avoid placing hazardous...
and robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
. For sets of four points in the plane, the geometric median coincides with the Radon point.
Another generalization for partition into r sets was given by and is now known as Tverberg's theorem
Tverberg's theorem
In discrete geometry, Tverberg's theorem, first stated by , is the result that sufficiently many points in d-dimensional Euclidean space can be partitioned into subsets with intersecting convex hulls...
. It states that for any set of
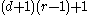
points in Euclidean d-space, there is a partition into r subsets whose convex hulls intersect in at least one common point.
Carathéodory's theorem
Carathéodory's theorem (convex hull)
In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
states that any point in the convex hull of some set of points is also within the convex hull of a subset of at most d + 1 of the points; that is, that the given point is part of a Radon partition in which it is a singleton. One proof of Carathéodory's theorem uses a technique of examining solutions to systems of linear equations, similar to the proof of Radon's theorem, to eliminate one point at a time until at most d + 1 remain.
Concepts related to Radon's theorem have also been considered for convex geometries
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
, families of finite sets with the properties that the intersection of any two sets in the family remains in the family, and that the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and the union of all the sets belongs to the family. In this more general context, the convex hull of a set S is the intersection of the family members that contain S, and the Radon number of a space is the smallest r such that any r points have two subsets whose convex hulls intersect. Similarly, one can define the Helly number h and the Carathéodory number c by analogy to their definitions for convex sets in Euclidean spaces, and it can be shown that these numbers satisfy the inequalities h < r ≤ ch + 1.
In an arbitrary undirected graph, one may define a convex set to be a set of vertices that includes every induced path
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
connecting a pair of vertices in the set. With this definition, every set of ω + 1 vertices in the graph can be partitioned into two subsets whose convex hulls intersect, and ω + 1 is the minimum number for which this is possible, where ω is the clique number of the given graph. For related results involving shortest paths instead of induced paths see and .