Q-difference polynomial
Encyclopedia
In combinatorial
mathematics
, the q-difference polynomials or q-harmonic polynomials are a polynomial sequence
defined in terms of the q-derivative
. They are a type of Brenke polynomial, and generalize the Appell polynomials. See also Sheffer sequence.
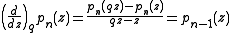
where the derivative symbol on the left is the q-derivative. In the limit of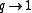
, this becomes the definition of the Appell polynomials:
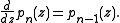
for these polynomials is of the type of generating function for Brenke polynomials, namely
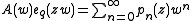
where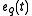
is the q-exponential: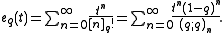
Here,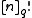
is the q-factorial and
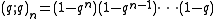
is the q-Pochhammer symbol. The function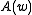
is arbitrary but assumed to have an expansion
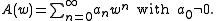
Any such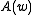
gives a sequence of q-difference polynomials.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the q-difference polynomials or q-harmonic polynomials are a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
defined in terms of the q-derivative
Q-derivative
In mathematics, in the area of combinatorics, the q-derivative, or Jackson derivative, is a q-analog of the ordinary derivative, introduced by Frank Hilton Jackson. It is the inverse of Jackson's q-integration-Definition:...
. They are a type of Brenke polynomial, and generalize the Appell polynomials. See also Sheffer sequence.
Definition
The q-difference polynomials satisfy the relation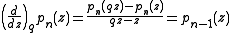where the derivative symbol on the left is the q-derivative. In the limit of
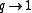, this becomes the definition of the Appell polynomials: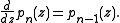Generating function
The generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for these polynomials is of the type of generating function for Brenke polynomials, namely
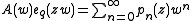
where
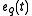is the q-exponential: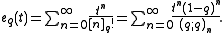Here,
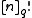is the q-factorial and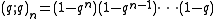is the q-Pochhammer symbol. The function
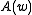is arbitrary but assumed to have an expansion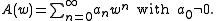Any such
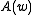gives a sequence of q-difference polynomials.