
Power sum symmetric polynomial
Encyclopedia
In mathematics
, specifically in commutative algebra
, the power sum symmetric polynomials are a type of basic building block for symmetric polynomial
s, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
 variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers
variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers
of the variables. Formally,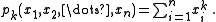
The first few of these polynomials are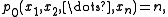
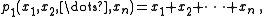

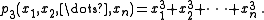
Thus, for each nonnegative integer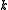 , there exists exactly one power sum symmetric polynomial of degree
, there exists exactly one power sum symmetric polynomial of degree 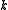 in
in  variables.
variables.
The polynomial ring
formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring
.
 power sum symmetric polynomials of positive degrees up to n for the first three positive values of
power sum symmetric polynomials of positive degrees up to n for the first three positive values of  In every case,
In every case, 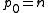 is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
For n = 1: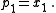
For n = 2: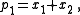
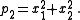
For n = 3: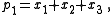
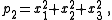
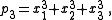
of symmetric polynomial
s in n variables. More specifically:
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial
has the expression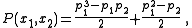
which involves fractions. According to the theorem this is the only way to represent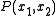 in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring
in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring 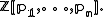
For another example, the elementary symmetric polynomial
s ek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,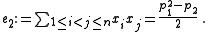
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then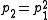 , so p1 and p2 cannot generate e2 = x1x2.
, so p1 and p2 cannot generate e2 = x1x2.
Sketch of a partial proof of the theorem: By Newton's identities
the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence
, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities
):
Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):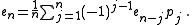
This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n.
Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function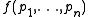 of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, 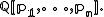 Because every power sum polynomial is symmetric, the two rings are equal.
Because every power sum polynomial is symmetric, the two rings are equal.
(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomial
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the power sum symmetric polynomials are a type of basic building block for symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
Definition
The power sum symmetric polynomial of degree k in variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powers
variables x1, ..., xn, written pk for k = 0, 1, 2, ..., is the sum of all kth powersExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of the variables. Formally,
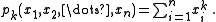
The first few of these polynomials are
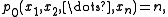
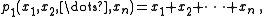

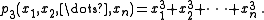
Thus, for each nonnegative integer
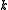 , there exists exactly one power sum symmetric polynomial of degree
, there exists exactly one power sum symmetric polynomial of degree 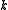 in
in  variables.
variables.The polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
formed by taking all integral linear combinations of products of the power sum symmetric polynomials is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.
Examples
The following lists the power sum symmetric polynomials of positive degrees up to n for the first three positive values of
power sum symmetric polynomials of positive degrees up to n for the first three positive values of  In every case,
In every case, 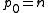 is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.
is one of the polynomials. The list goes up to degree n because the power sum symmetric polynomials of degrees 1 to n are basic in the sense of the Main Theorem stated below.For n = 1:
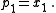
For n = 2:
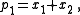
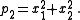
For n = 3:
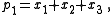
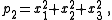
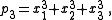
Properties
The set of power sum symmetric polynomials of degrees 1, 2, ..., n in n variables generates the ringPolynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
of symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
s in n variables. More specifically:
- Theorem. The ring of symmetric polynomials with rational coefficients equals the rational polynomial ring
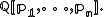 The same is true if the coefficients are taken in any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
The same is true if the coefficients are taken in any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
whose characteristic is 0.
However, this is not true if the coefficients must be integers. For example, for n = 2, the symmetric polynomial

has the expression
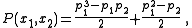
which involves fractions. According to the theorem this is the only way to represent
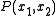 in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring
in terms of p1 and p2. Therefore, P does not belong to the integral polynomial ring 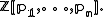
For another example, the elementary symmetric polynomial
Elementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s ek, expressed as polynomials in the power sum polynomials, do not all have integral coefficients. For instance,
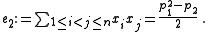
The theorem is also untrue if the field has characteristic different from 0. For example, if the field F has characteristic 2, then
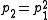 , so p1 and p2 cannot generate e2 = x1x2.
, so p1 and p2 cannot generate e2 = x1x2.Sketch of a partial proof of the theorem: By Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
the power sums are functions of the elementary symmetric polynomials; this is implied by the following recurrence
Recurrence
Recurrence and recurrent may refer to:*Recurrence relation, an equation which defines a sequence recursively*Poincaré recurrence theorem, Henri Poincaré's theorem on dynamical systems...
, though the explicit function that gives the power sums in terms of the ej is complicated (see Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
):

Rewriting the same recurrence, one has the elementary symmetric polynomials in terms of the power sums (also implicitly, the explicit formula being complicated):
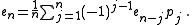
This implies that the elementary polynomials are rational, though not integral, linear combinations of the power sum polynomials of degrees 1, ..., n.
Since the elementary symmetric polynomials are an algebraic basis for all symmetric polynomials with coefficients in a field, it follows that every symmetric polynomial in n variables is a polynomial function
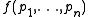 of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums,
of the power sum symmetric polynomials p1, ..., pn. That is, the ring of symmetric polynomials is contained in the ring generated by the power sums, 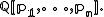 Because every power sum polynomial is symmetric, the two rings are equal.
Because every power sum polynomial is symmetric, the two rings are equal.(This does not show how to prove the polynomial f is unique.)
For another system of symmetric polynomials with similar properties see complete homogeneous symmetric polynomial
Complete homogeneous symmetric polynomial
In mathematics, specifically in algebraic combinatorics and commutative algebra, the complete homogeneous symmetric polynomials are a specific kind of symmetric polynomials...
s.

