Discussion
Ask a question about 'Polynomials on vector spaces' Start a new discussion about 'Polynomials on vector spaces' Answer questions from other users |
In
mathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if
F is a field, a single-variable
F-valued
polynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of
degreeThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
≤
p on a
vector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is a
mapIn mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
P :
V →
F of the form
-
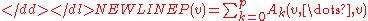
for v ∈ V and Ak ∈ Lksym = the set of all F-valued symmetric k-linear formsIn linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
for k = 0, ..., p. P is called homogeneous of degree p if P = Ap above.
Similarly, one can define an n-variable F-valued polynomial of degree ≤ p on V to be
-
where Ai,j,k ∈ Lpi,j,ksym with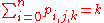 
. In this case P is called homogeneous if we only have the k = p summand in the above expression.