Pointclass
Encyclopedia
In the mathematical field of descriptive set theory
, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space
. In practice, a pointclass is usually characterized by some sort of definability property; for example, the collection of all open set
s in some fixed collection of Polish spaces is a pointclass. (An open set may be seen as in some sense definable because it cannot be a purely arbitrary collection of points; for any point in the set, all points sufficiently close to that point must also be in the set.)
Pointclasses find application in formulating many important principles and theorems from set theory
and real analysis
. Strong set-theoretic principles may be stated in terms of the determinacy
of various pointclasses, which in turn implies that sets in those pointclasses (or sometimes larger ones) have regularity properties such as Lebesgue measurability
(and indeed universal measurability
), the property of Baire, and the perfect set property
.
or sometimes Cantor space
, each of which has the advantage of being zero dimensional, and indeed homeomorphic to its finite or countable powers, so that considerations of dimensionality never arise. Moschovakis
provides greater generality by fixing once and for all a collection of underlying Polish spaces, including the set of all naturals, the set of all reals, Baire space, and Cantor space, and otherwise allowing the reader to throw in any desired perfect Polish space. Then he defines a product space to be any finite Cartesian product
of these underlying spaces. Then, for example, the pointclass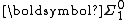
of all open sets means the collection of all open subsets of one of these product spaces. This approach prevents 
from being a proper class, while avoiding excessive specificity as to the particular Polish spaces being considered (given that the focus is on the fact that 
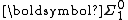is the collection of open sets, not on the spaces themselves).
, and in the more complex projective hierarchy, are represented by sub- and super-scripted Greek letters in boldface fonts; for example,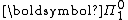
is the pointclass of all closed set
s,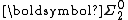
is the pointclass of all Fσ sets, 
is the collection of all sets that are simultaneously Fσ and Gδ
, and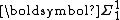
is the pointclass of all analytic set
s.
Sets in such pointclasses need be "definable" only up to a point. For example, every singleton set in a Polish space is closed, and thus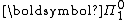
. Therefore it cannot be that every 
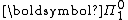set must be "more definable" than an arbitrary element of a Polish space (say, an arbitrary real number, or an arbitrary countable sequence of natural numbers). Boldface pointclasses, however, may (and in practice ordinarily do) require that sets in the class be definable relative to some real number, taken as an oracle
. In that sense, membership in a boldface pointclass is a definability property, even though it is not absolute definability, but only definability with respect to a possibly undefinable real number.
Boldface pointclasses, or at least the ones ordinarily considered, are closed under Wadge reducibility; that is, given a set in the pointclass, its inverse image under a continuous function
(from a product space to the space of which the given set is a subset) is also in the given pointclass. Thus a boldface pointclass is a downward-closed union of Wadge degrees.
in which the definability property is no longer relativized to an oracle, but is made absolute. For example, if one fixes some collection of basic open neighborhoods (say, in Baire space, the set of all sets of the form {x∈ωω|x ⊇s} for any fixed finite sequence s of natural numbers), then the open, or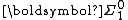
, sets may be characterized as all (arbitrary) unions of basic open neighborhoods. The analogous 
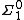sets, with a lightface 
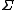, are no longer arbitrary unions of such neighborhoods, but computable unions of them (that is, a set is 
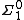if there is a computable set S of finite sequences of naturals such that the given set is the union of all {x∈ωω|x ⊇s} for s in S). A set is lightface 
if it is the complement of a 
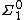set. Thus each 
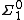set has at least one index, which describes the computable function enumerating the basic open sets from which it is composed; in fact it will have infinitely many such indices. Similarly, an index for a 
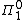set B describes the computable function enumerating the basic open sets in the complement of B.
A set A is lightface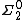
if it is a union of a computable sequence of 
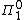sets (that is, there is a computable enumeration of indices of 
sets such that A is the union of these sets). This relationship between lightface sets and their indices is used to extend the lightface Borel hierarchy into the transfinite, via recursive ordinal
s. This produces that hyperarithmetic hierarchy, which is the lightface analog of the Borel hierarchy. (The finite levels of the hyperarithmetic hierarchy
are known as the arithmetical hierarchy
.)
A similar treatment can be applied to the projective hierarchy. Its lightface analog is known as the analytical hierarchy
.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
. In practice, a pointclass is usually characterized by some sort of definability property; for example, the collection of all open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in some fixed collection of Polish spaces is a pointclass. (An open set may be seen as in some sense definable because it cannot be a purely arbitrary collection of points; for any point in the set, all points sufficiently close to that point must also be in the set.)
Pointclasses find application in formulating many important principles and theorems from set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
. Strong set-theoretic principles may be stated in terms of the determinacy
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
of various pointclasses, which in turn implies that sets in those pointclasses (or sometimes larger ones) have regularity properties such as Lebesgue measurability
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
(and indeed universal measurability
Universally measurable set
In mathematics, a subset A of a Polish space X is universally measurable if it is measurable with respect to every complete probability measure on X that measures all Borel subsets of X. In particular, a universally measurable set of reals is necessarily Lebesgue measurable below.Every analytic...
), the property of Baire, and the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
.
Basic framework
In practice, descriptive set theorists often simplify matters by working in a fixed Polish space such as Baire spaceBaire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
or sometimes Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
, each of which has the advantage of being zero dimensional, and indeed homeomorphic to its finite or countable powers, so that considerations of dimensionality never arise. Moschovakis
Yiannis N. Moschovakis
Yiannis Nicholas Moschovakis is a set theorist, descriptive set theorist, and recursion theorist, at UCLA. For many years he has split his time between UCLA and University of Athens . His book Descriptive Set Theory is the primary reference for the subject...
provides greater generality by fixing once and for all a collection of underlying Polish spaces, including the set of all naturals, the set of all reals, Baire space, and Cantor space, and otherwise allowing the reader to throw in any desired perfect Polish space. Then he defines a product space to be any finite Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of these underlying spaces. Then, for example, the pointclass
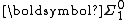of all open sets means the collection of all open subsets of one of these product spaces. This approach prevents from being a proper class, while avoiding excessive specificity as to the particular Polish spaces being considered (given that the focus is on the fact that 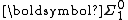is the collection of open sets, not on the spaces themselves).Boldface pointclasses
The pointclasses in the Borel hierarchyBorel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
, and in the more complex projective hierarchy, are represented by sub- and super-scripted Greek letters in boldface fonts; for example,
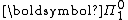is the pointclass of all closed setClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s,
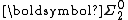is the pointclass of all Fσ sets, is the collection of all sets that are simultaneously Fσ and GδG-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
, and
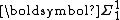is the pointclass of all analytic setAnalytic set
In descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set...
s.
Sets in such pointclasses need be "definable" only up to a point. For example, every singleton set in a Polish space is closed, and thus
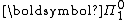. Therefore it cannot be that every 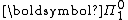set must be "more definable" than an arbitrary element of a Polish space (say, an arbitrary real number, or an arbitrary countable sequence of natural numbers). Boldface pointclasses, however, may (and in practice ordinarily do) require that sets in the class be definable relative to some real number, taken as an oracleOracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
. In that sense, membership in a boldface pointclass is a definability property, even though it is not absolute definability, but only definability with respect to a possibly undefinable real number.
Boldface pointclasses, or at least the ones ordinarily considered, are closed under Wadge reducibility; that is, given a set in the pointclass, its inverse image under a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(from a product space to the space of which the given set is a subset) is also in the given pointclass. Thus a boldface pointclass is a downward-closed union of Wadge degrees.
Lightface pointclasses
The Borel and projective hierarchies have analogs in effective descriptive set theoryEffective descriptive set theory
Effective descriptive set theory is the branch of descriptive set theory dealing with sets of reals having lightface definitions; that is, definitions that do not require an arbitrary real parameter. Thus effective descriptive set theory combines descriptive set theory with recursion theory....
in which the definability property is no longer relativized to an oracle, but is made absolute. For example, if one fixes some collection of basic open neighborhoods (say, in Baire space, the set of all sets of the form {x∈ωω|x ⊇s} for any fixed finite sequence s of natural numbers), then the open, or
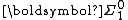, sets may be characterized as all (arbitrary) unions of basic open neighborhoods. The analogous 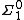sets, with a lightface 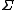, are no longer arbitrary unions of such neighborhoods, but computable unions of them (that is, a set is 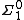if there is a computable set S of finite sequences of naturals such that the given set is the union of all {x∈ωω|x ⊇s} for s in S). 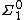A set is lightface if it is the complement of a set. Thus each 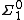set has at least one index, which describes the computable function enumerating the basic open sets from which it is composed; in fact it will have infinitely many such indices. Similarly, an index for a 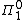set B describes the computable function enumerating the basic open sets in the complement of B.A set A is lightface
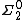if it is a union of a computable sequence of 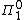sets (that is, there is a computable enumeration of indices of sets such that A is the union of these sets). This relationship between lightface sets and their indices is used to extend the lightface Borel hierarchy into the transfinite, via recursive ordinalRecursive ordinal
In mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
s. This produces that hyperarithmetic hierarchy, which is the lightface analog of the Borel hierarchy. (The finite levels of the hyperarithmetic hierarchy
Hyperarithmetical theory
In recursion theory, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic and with weak systems of set theory such as Kripke–Platek set theory...
are known as the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
.)
A similar treatment can be applied to the projective hierarchy. Its lightface analog is known as the analytical hierarchy
Analytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
.