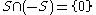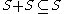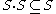Partially-ordered ring
Encyclopedia
In abstract algebra
, a partially-ordered ring is a ring
(A, +, · ), together with a compatible partial order, i.e. a partial order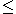 on the underlying set A that is compatible with the ring operations in the sense that it satisfies:
on the underlying set A that is compatible with the ring operations in the sense that it satisfies: implies
implies 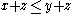
and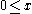 and
and 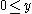 imply that
imply that 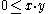
for all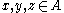 . Various extensions of this definition exist that constrain the ring, the partial order, or both. For example, an Archimedean partially-ordered ring is a partially-ordered ring
. Various extensions of this definition exist that constrain the ring, the partial order, or both. For example, an Archimedean partially-ordered ring is a partially-ordered ring 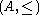 where
where 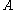 's partially-ordered additive group is Archimedean
's partially-ordered additive group is Archimedean
.
An ordered ring, also called a totally-ordered ring, is a partially-ordered ring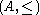 where
where 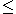 is additionally a total order
is additionally a total order
.
An l-ring, or lattice-ordered ring, is a partially-ordered ring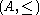 where
where 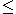 is additionally a lattice order.
is additionally a lattice order.
The set of non-negative elements of a partially ordered ring (the set of elements x for which , also called the positive cone of the ring) is closed under addition and multiplication, i.e., if P is the set of non-negative elements of a partially ordered ring, then
, also called the positive cone of the ring) is closed under addition and multiplication, i.e., if P is the set of non-negative elements of a partially ordered ring, then 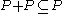 , and
, and 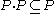 . Furthermore,
. Furthermore,  .
.
The mapping of the compatible partial order on a ring A to the set of its non-negative elements is one-to-one; that is, the compatible partial order uniquely determines the set of non-negative elements, and a set of elements uniquely determines the compatible partial order if one exists.
If S is a subset of a ring A, and:
then the relation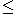 where
where 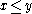 iff
iff
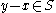 defines a compatible partial order on A (ie.
defines a compatible partial order on A (ie.  is a partially-ordered ring).
is a partially-ordered ring).
In any l-ring, the absolute value of an element x can be defined to be
of an element x can be defined to be 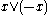 , where
, where 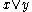 denotes the maximal element
denotes the maximal element
. For any x and y,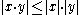
holds.
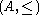 in which
in which 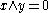 and
and  imply that
imply that 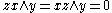 for all
for all 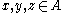 . They were first introduced by Garrett Birkhoff
. They were first introduced by Garrett Birkhoff
and Richard S. Pierce in 1956, in a paper titled "Lattice-ordered rings", in an attempt to restrict the class of l-rings so as to eliminate a number of pathological examples. For example, Birkhoff and Pierce demonstrated an l-ring with 1 in which 1 is negative, even though being a square. The additional hypothesis required of f-rings eliminates this possibility.
, and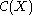 be the space of all continuous
be the space of all continuous
, real
-valued function
s on X.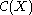 is an Archimedean f-ring with 1 under the following point-wise operations:
is an Archimedean f-ring with 1 under the following point-wise operations: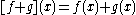
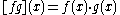
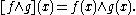
From an algebraic point of view the rings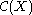
are fairly rigid. For example localisations, residue rings or limits of
rings of the form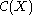 are not of this form in general.
are not of this form in general.
A much more flexible class of f-rings containing all rings of continuous functions
and resembling many of the properties of these rings, is the class of real closed ring
s.
of f-rings is an f-ring, an l-subring of an f-ring is an f-ring, and an l-homomorphic image
of an f-ring is an f-ring.
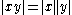 in an f-ring.
in an f-ring.
The category
Arf consists of the Archimedean f-rings with 1 and the l-homomorphisms that preserve the identity.
Every ordered ring is an f-ring, so every subdirect union of ordered rings is also an f-ring. Assuming the axiom of choice, a theorem of Birkhoff shows the converse, and that an l-ring is an f-ring if and only if it is l-isomorphic to a subdirect union of ordered rings. Some mathematicians take this to be the definition of an f-ring.
ordered rings. The results are proved in the ring1 context.
Suppose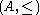 is a commutative ordered ring, and
is a commutative ordered ring, and 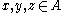 . Then:
. Then:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a partially-ordered ring is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(A, +, · ), together with a compatible partial order, i.e. a partial order
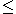 on the underlying set A that is compatible with the ring operations in the sense that it satisfies:
on the underlying set A that is compatible with the ring operations in the sense that it satisfies: implies
implies 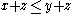
and
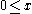 and
and 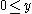 imply that
imply that 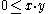
for all
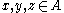 . Various extensions of this definition exist that constrain the ring, the partial order, or both. For example, an Archimedean partially-ordered ring is a partially-ordered ring
. Various extensions of this definition exist that constrain the ring, the partial order, or both. For example, an Archimedean partially-ordered ring is a partially-ordered ring 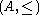 where
where 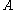 's partially-ordered additive group is Archimedean
's partially-ordered additive group is ArchimedeanArchimedean group
In abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...
.
An ordered ring, also called a totally-ordered ring, is a partially-ordered ring
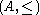 where
where 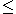 is additionally a total order
is additionally a total orderTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.
An l-ring, or lattice-ordered ring, is a partially-ordered ring
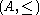 where
where 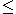 is additionally a lattice order.
is additionally a lattice order.Properties
The additive group of a partially-ordered ring is always a partially-ordered group.The set of non-negative elements of a partially ordered ring (the set of elements x for which
 , also called the positive cone of the ring) is closed under addition and multiplication, i.e., if P is the set of non-negative elements of a partially ordered ring, then
, also called the positive cone of the ring) is closed under addition and multiplication, i.e., if P is the set of non-negative elements of a partially ordered ring, then 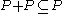 , and
, and 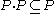 . Furthermore,
. Furthermore,  .
.The mapping of the compatible partial order on a ring A to the set of its non-negative elements is one-to-one; that is, the compatible partial order uniquely determines the set of non-negative elements, and a set of elements uniquely determines the compatible partial order if one exists.
If S is a subset of a ring A, and:
then the relation
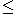 where
where 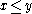 iff
iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
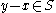 defines a compatible partial order on A (ie.
defines a compatible partial order on A (ie.  is a partially-ordered ring).
is a partially-ordered ring).In any l-ring, the absolute value
 of an element x can be defined to be
of an element x can be defined to be 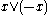 , where
, where 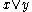 denotes the maximal element
denotes the maximal elementMaximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
. For any x and y,
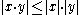
holds.
f-rings
An f-ring, or Pierce–Birkhoff ring, is a lattice-ordered ring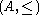 in which
in which 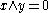 and
and  imply that
imply that 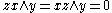 for all
for all 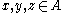 . They were first introduced by Garrett Birkhoff
. They were first introduced by Garrett BirkhoffGarrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
and Richard S. Pierce in 1956, in a paper titled "Lattice-ordered rings", in an attempt to restrict the class of l-rings so as to eliminate a number of pathological examples. For example, Birkhoff and Pierce demonstrated an l-ring with 1 in which 1 is negative, even though being a square. The additional hypothesis required of f-rings eliminates this possibility.
Example
Let X be a Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, and
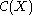 be the space of all continuous
be the space of all continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s on X.
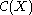 is an Archimedean f-ring with 1 under the following point-wise operations:
is an Archimedean f-ring with 1 under the following point-wise operations: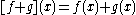
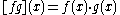
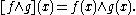
From an algebraic point of view the rings
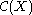
are fairly rigid. For example localisations, residue rings or limits of
rings of the form
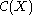 are not of this form in general.
are not of this form in general.A much more flexible class of f-rings containing all rings of continuous functions
and resembling many of the properties of these rings, is the class of real closed ring
Real closed ring
In mathematics, a real closed ring is a commutative ring A thatis a subring of a product of real closed fields, which is closed undercontinuous semi-algebraic functions defined over the integers.- Examples of real closed rings :...
s.
Properties
A direct productDirect product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of f-rings is an f-ring, an l-subring of an f-ring is an f-ring, and an l-homomorphic image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of an f-ring is an f-ring.
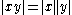 in an f-ring.
in an f-ring.The category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
Arf consists of the Archimedean f-rings with 1 and the l-homomorphisms that preserve the identity.
Every ordered ring is an f-ring, so every subdirect union of ordered rings is also an f-ring. Assuming the axiom of choice, a theorem of Birkhoff shows the converse, and that an l-ring is an f-ring if and only if it is l-isomorphic to a subdirect union of ordered rings. Some mathematicians take this to be the definition of an f-ring.
Formally-verified results for commutative ordered rings
IsarMathLib, a library for the Isabelle theorem prover, has formal verifications of a few fundamental results on commutativeCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
ordered rings. The results are proved in the ring1 context.
Suppose
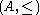 is a commutative ordered ring, and
is a commutative ordered ring, and 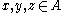 . Then:
. Then:| by | |
|---|---|
| The additive group of A is an ordered group | OrdRing_ZF_1_L4 |
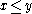 iff iff  |
OrdRing_ZF_1_L7 |
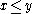 and and 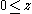 imply imply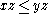 and and 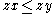 |
OrdRing_ZF_1_L9 |
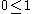 |
ordring_one_is_nonneg |
| OrdRing_ZF_2_L5 | |
| ord_ring_triangle_ineq | |
| x is either in the positive set, equal to 0, or in minus the positive set. | OrdRing_ZF_3_L2 |
The set of positive elements of 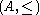 is closed under multiplication iff A has no zero divisor is closed under multiplication iff A has no zero divisorZero divisor In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply... s. |
OrdRing_ZF_3_L3 |
If A is non-trivial (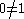 ), then it is infinite. ), then it is infinite. |
ord_ring_infinite |
Further reading
- Gillman, Leonard; Jerison, MeyerMeyer JerisonMeyer Jerison was an American mathematician known for his work in functional analysis and rings, and especially for collaborating with Leonard Gillman on one of the standard texts in the field: Rings of Continuous Functions.-Biography:...
Rings of continuous functions. Reprint of the 1960 edition. Graduate Texts in Mathematics, No. 43. Springer-Verlag, New York-Heidelberg, 1976. xiii+300 pp