
Partial equivalence relation
Encyclopedia
In mathematics
, a partial equivalence relation (often abbreviated as PER) on a set
on a set  is a relation that is symmetric
is a relation that is symmetric
and transitive
. In other words, it holds for all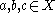 that:
that:
If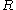 is also reflexive
is also reflexive
, then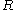 is an equivalence relation
is an equivalence relation
.
In a set-theoretic context, there is a simple structure to the general PER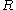 on
on 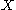 : it is an equivalence relation on the subset
: it is an equivalence relation on the subset 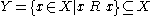 . (
. ( is the subset of
is the subset of 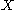 such that in the complement
such that in the complement
of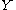 (
(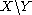 ) no element is related by
) no element is related by 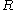 to any other.) By construction,
to any other.) By construction, 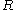 is reflexive on
is reflexive on 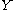 and therefore an equivalence relation on
and therefore an equivalence relation on  . Notice that
. Notice that 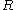 is actually only true on elements of
is actually only true on elements of  : if
: if  , then
, then 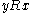 by symmetry, so
by symmetry, so 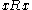 and
and 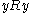 by transitivity. Conversely, given a subset Y of X, any equivalence relation on Y is automatically a PER on X.
by transitivity. Conversely, given a subset Y of X, any equivalence relation on Y is automatically a PER on X.
PERs are therefore used mainly in computer science
, type theory
and constructive mathematics, particularly to define setoid
s, sometimes called partial setoids. The action of forming one from a type and a PER is analogous to the operations of subset and quotient in classical set-theoretic mathematics.
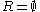 (unless
(unless 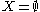 , in which case the empty relation is an equivalence relation (and is the only relation on
, in which case the empty relation is an equivalence relation (and is the only relation on 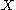 )).
)).
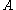 and a partial function
and a partial function  that is defined on some elements of
that is defined on some elements of 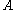 but not all. Then the relation
but not all. Then the relation 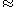 defined by
defined by
is a partial equivalence relation but not an equivalence relation. It possesses the symmetry and transitivity properties, but it is not reflexive since if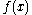 is not defined then
is not defined then 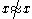 — in fact, for such an
— in fact, for such an  there is no
there is no 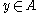 such that
such that 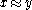 . (It follows immediately that the subset of
. (It follows immediately that the subset of  for which
for which  is an equivalence relation is precisely the subset on which
is an equivalence relation is precisely the subset on which 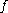 is defined.)
is defined.)
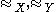 . For
. For 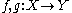 , define
, define 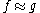 to mean:
to mean:
then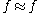 means that f induces a well-defined function of the quotients
means that f induces a well-defined function of the quotients 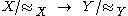 . Thus, the PER
. Thus, the PER 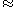 captures both the idea of definedness on the quotients and of two functions inducing the same function on the quotient.
captures both the idea of definedness on the quotients and of two functions inducing the same function on the quotient.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a partial equivalence relation (often abbreviated as PER)
 on a set
on a set  is a relation that is symmetric
is a relation that is symmetricSymmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
. In other words, it holds for all
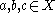 that:
that:- if
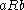 , then
, then 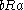 (symmetry)
(symmetry) - if
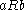 and
and 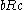 , then
, then 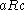 (transitivity)
(transitivity)
If
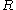 is also reflexive
is also reflexiveReflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, then
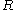 is an equivalence relation
is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
In a set-theoretic context, there is a simple structure to the general PER
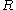 on
on 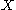 : it is an equivalence relation on the subset
: it is an equivalence relation on the subset 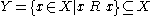 . (
. ( is the subset of
is the subset of 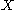 such that in the complement
such that in the complementComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of
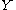 (
(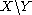 ) no element is related by
) no element is related by 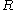 to any other.) By construction,
to any other.) By construction, 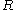 is reflexive on
is reflexive on 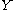 and therefore an equivalence relation on
and therefore an equivalence relation on  . Notice that
. Notice that 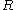 is actually only true on elements of
is actually only true on elements of  : if
: if  , then
, then 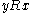 by symmetry, so
by symmetry, so 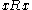 and
and 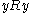 by transitivity. Conversely, given a subset Y of X, any equivalence relation on Y is automatically a PER on X.
by transitivity. Conversely, given a subset Y of X, any equivalence relation on Y is automatically a PER on X.PERs are therefore used mainly in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
and constructive mathematics, particularly to define setoid
Setoid
In mathematics, a setoid is a set equipped with an equivalence relation.Setoids are studied especially in proof theory and in type-theoretic foundations of mathematics. Often in mathematics, when one defines an equivalence relation on a set, one immediately forms the quotient set...
s, sometimes called partial setoids. The action of forming one from a type and a PER is analogous to the operations of subset and quotient in classical set-theoretic mathematics.
Examples
A simple example of a PER that is not an equivalence relation is the empty relation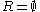 (unless
(unless 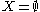 , in which case the empty relation is an equivalence relation (and is the only relation on
, in which case the empty relation is an equivalence relation (and is the only relation on 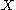 )).
)).Kernels of partial functions
For another example of a PER, consider a set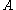 and a partial function
and a partial function  that is defined on some elements of
that is defined on some elements of 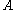 but not all. Then the relation
but not all. Then the relation 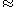 defined by
defined by
-
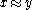 if and only if
if and only if  is defined at
is defined at  ,
, 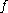 is defined at
is defined at 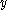 , and
, and 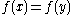
is a partial equivalence relation but not an equivalence relation. It possesses the symmetry and transitivity properties, but it is not reflexive since if
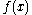 is not defined then
is not defined then 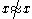 — in fact, for such an
— in fact, for such an  there is no
there is no 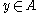 such that
such that 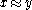 . (It follows immediately that the subset of
. (It follows immediately that the subset of  for which
for which  is an equivalence relation is precisely the subset on which
is an equivalence relation is precisely the subset on which 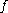 is defined.)
is defined.)Functions respecting equivalence relations
Let X and Y be sets equipped with equivalence relations (or PERs)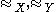 . For
. For 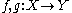 , define
, define 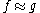 to mean:
to mean:then
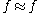 means that f induces a well-defined function of the quotients
means that f induces a well-defined function of the quotients 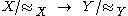 . Thus, the PER
. Thus, the PER 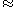 captures both the idea of definedness on the quotients and of two functions inducing the same function on the quotient.
captures both the idea of definedness on the quotients and of two functions inducing the same function on the quotient.Reference
- Mitchell, John C. Foundations of programming languages. MIT Press, 1996.
See also
- Equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
- Binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...


