Opening (morphology)

In mathematical morphology

Mathematical morphology

Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...

, opening is the dilation

Dilation (morphology)

Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...

 of the erosion

Erosion (morphology)

For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...

 of a set A by a structuring element

Structuring element

In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image...

 B:


where and denote erosion and dilation, respectively.

Together with closing

Closing (morphology)

In mathematical morphology, the closing of a set A by a structuring element B is the erosion of the dilation of that set,A\bullet B = \ominus B, \, where \oplus and \ominus denote the dilation and erosion, respectively....

, the opening serves in computer vision

Computer vision

Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...

 and image processing

Image processing

In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...

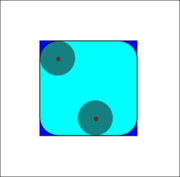
 as a basic workhorse of morphological noise removal. Opening removes small objects from the foreground (usually taken as the dark pixels) of an image, placing them in the background, while closing removes small holes in the foreground, changing small islands of background into foreground. These techniques can also be used to find specific shapes in an image. Opening can be used to find things into which a specific structuring element can fit (edges, corners, ...).

One can think of B sweeping around the inside of the boundary of A, so that it does not extend beyond the boundary, and shaping the A boundary around the boundary of the element.

Properties

• Opening is idempotent, that is, .
• Opening is increasing, that is, if , then .
• Opening is anti-extensive, i.e., .
• Opening is translation invariant.
• Opening and closing satisfy the duality , where denotes closing.

See also

• Mathematical morphology
  Mathematical morphology
  Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
  
  
• Closing
  Closing (morphology)
  In mathematical morphology, the closing of a set A by a structuring element B is the erosion of the dilation of that set,A\bullet B = \ominus B, \, where \oplus and \ominus denote the dilation and erosion, respectively....
  
  
• Dilation
  Dilation (morphology)
  Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...
  
  
• Erosion
  Erosion (morphology)
  For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...