In abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

, a subset of a ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

 is said to be multiplicatively closed if it is closed

Closure (mathematics)

In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...

 under multiplication (i.e., xy is in the set when x and y are in it) and contains 1 but doesn't contain 0. The condition is especially important in commutative algebra

Commutative algebra

Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...

, where multiplicatively closed sets are used to build localization

Localization

Localization or localisation, and represented as a numeronym as L10n, may refer to:* Language localization, the process of translating a product into different languages or adapting a product for a specific country or region...

s of commutative rings.

Examples

Common examples of multiplicatively closed sets include:

1. the se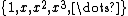t where x is not a nilpotent element;
2. the set of unit
   Unit (ring theory)
   In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
   
   s of the ring;
3. the set of regular element
   Zero divisor
   In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
   
   s of the ring;
4. in a commutative ring, the set-theoretic complement of a prime ideal
   Prime ideal
   In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
   
   .

Properties

For commutative rings, the complement of a prime ideal is an especially important example of a multiplicatively closed set. Clearly an ideal A of a commutative ring R is prime if and only if the complement R\A is multiplicatively closed. In fact, complements of prime ideals enjoy another property: that of being "saturated". A set is said to be saturated if every divisor

Divisibility (ring theory)

In mathematics, the notion of a divisor originally arose within the context of arithmetic of whole numbers. Please see the page about divisors for this simplest example. With the development of abstract rings, of which the integers are the archetype, the original notion of divisor found a natural...

 of x in the set is also in the set (i.e., if xy is in the set, then x and y are in the set). For a commutative ring the converse is not always true: a saturated multiplicative set may not be a complement of a prime ideal. However it is true that a subset S is saturated and multiplicatively closed if and only if S is the set-theoretic complement of a non-empty set-theoretic union of prime ideals, .

The intersection of a family of multiplicative sets is again multiplicative, and the intersection of a family of saturated sets is saturated.

Suppose S is a multiplicatively closed subset of a commutative ring R. A standard lemma due to Krull states that there exists an ideal P of R maximal with respect to having empty intersection with S, and this ideal is a prime ideal. It follows that S is a subset of the complement R\P, which is a saturated multiplicatively closed set. Thus every multiplicatively closed set is a subset of a saturated multiplicatively closed set.