
Morse homology
Encyclopedia
In mathematics
, specifically in the field of differential topology
, Morse homology is a homology theory
defined for any smooth manifold
. It is constructed using the smooth structure
and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to singular homology
. Morse homology also serves as a model for the various infinite-dimensional generalizations known as Floer homology
theories.
vector field. We say that (f, g) is Morse-Smale if the stable
and unstable manifolds associated to all of the critical points
of f intersect each other transversely
.
For any such (f, g), it can be shown that the difference in index
between any two critical points is equal to the dimension of the moduli space
of gradient flows between those points. Thus there is a one-dimensional moduli space of flows between a critical point of index i and one of index i − 1. Each flow can be reparametrized by a one-dimensional translation in the domain. After modding out by these reparametrizations, the quotient space
is zero-dimensional — that is, a collection of oriented
points representing unparametrized flow lines.
A chain complex
 may then be defined as follows. The set of chains is the Z
may then be defined as follows. The set of chains is the Z
-module
generated by the critical points. The differential d of the complex sends a critical point p of index i to a sum of index-(i − 1) critical points, with coefficients corresponding to the (signed) number of unparametrized flow lines from p to those index-(i − 1) critical points.
The fact that this defines a complex (that is, that d2 = 0) follows from an understanding of how the moduli spaces of gradient flows compactify
. Namely, in d2 p the coefficient of an index-(i − 2) critical point q is the (signed) number of broken flows consisting of an index-1 flow from p to some critical point r of index i − 1 and another index-1 flow from r to q. These broken flows exactly constitute the boundary of the moduli space of index-2 flows: The limit of any sequence of unbroken index-2 flows can be shown to be of this form, and all such broken flows arise as limits of unbroken index-2 flows. Unparametrized index-2 flows come in one-dimensional families, which compactify to compact one-manifolds. The fact that the boundary of a compact one-manifold is always zero proves that d2 p = 0.
analysis or by using a continuation map
to define a chain map from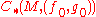 to
to 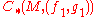 , it can be shown that the two Morse homologies are isomorphic. Analogous arguments using a homotopy of homotopies shows that this isomorphism is canonical.
, it can be shown that the two Morse homologies are isomorphic. Analogous arguments using a homotopy of homotopies shows that this isomorphism is canonical.
Another approach to proving the invariance of Morse homology is to relate it directly to singular homology. One can define a map to singular homology by sending a critical point to the singular chain associated to the unstable manifold associated to that point; inversely, a singular chain is sent to the limiting critical points reached by flowing the chain using the gradient vector field. The cleanest way to do this rigorously is to use the theory of currents
.
The isomorphism with singular homology can also be proved by demonstrating an isomorphism with cellular homology
, by viewing an unstable manifold associated to a critical point of index i as an i-cell, and showing that the boundary maps in the Morse and cellular complexes correspond.
and Stephen Smale
. It is also implicit in John Milnor
's book on the h-cobordism
theorem.
From the fact that the Morse homology is isomorphic to the singular homology, the Morse inequalities follow by considering the number of generators — that is, critical points — necessary to generate the homology groups of the appropriate ranks (and by considering truncations of the Morse complex, to get the stronger inequalities). The existence of Morse homology "explains", in the sense of categorification
, the Morse inequalities.
Edward Witten
came up with a related construction in the early 1980s sometimes known as Morse-Witten theory.
Morse homology can be extended to finite dimensional non-compact or infinite-dimensional manifolds where the index remains finite, the metric is complete and the function satisfies the Palais-Smale condition, such as the energy functional for geodesics on a Riemannian manifold. The generalization to situations in which both index and coindex are infinite, but the relative index of any pair of critical points is finite, is known as Floer homology
.
Sergei Novikov generalized this construction to a homology theory associated to a closed
one-form
on a manifold. Morse homology is a special case for the one-form df. A special case of Novikov's theory is circle-valued Morse theory
, which Michael Hutchings and Yi-Jen Lee have connected to Reidemeister torsion and Seiberg-Witten theory.
To describe the resulting chain complex and its homology, introduce a generic Morse function on each critical submanifold. Chains will consist of paths that begin in a critical manifold at a critical point of the auxiliary Morse function, following a gradient trajectory with respect to some metric, and then leave the submanifold to follow the gradient vector field of the Morse-Bott function until it hits some other critical manifold; it either flows for a while along a gradient trajectory associated to the Morse function on that critical submanifold and then flows to another critical submanifold, etc., or flows to a critical point in the original submanifold and terminates. See (Frauenfelder). This approach to Morse-Bott homology appeared in the context of contact homology in (Bourgeois), in which the critical submanifolds are the sets of Reeb orbits, and the gradient flows between the critical submanifolds are pseudoholomorphic curves in the symplectization of a contact manifold asymptotic to Reeb orbits in the relevant critical manifolds of Reeb orbits.
If we extend each Morse function to a function on the entire manifold supported near the critical submanifolds, we can explicitly write down a Morse-Smale function that perturbs the original Morse-Bott function. Namely, multiply each of the extended functions by some small positive constant, sum them and add the result to the original Morse-Bott function. The broken flows described above will be C0 close to the flow lines of this Morse-Smale function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in the field of differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, Morse homology is a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
defined for any smooth manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. It is constructed using the smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
. Morse homology also serves as a model for the various infinite-dimensional generalizations known as Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
theories.
Formal definition
Given any (compact) smooth manifold, let f be a Morse function and g a Riemannian metric on the manifold. (These are auxiliary; in the end, the Morse homology depends on neither.) The pair (f, g) gives us a gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
vector field. We say that (f, g) is Morse-Smale if the stable
Stable manifold
In mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
and unstable manifolds associated to all of the critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of f intersect each other transversely
Transversality
In mathematics, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency, and plays a role in general position. It formalizes the idea of a generic intersection in differential topology...
.
For any such (f, g), it can be shown that the difference in index
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
between any two critical points is equal to the dimension of the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of gradient flows between those points. Thus there is a one-dimensional moduli space of flows between a critical point of index i and one of index i − 1. Each flow can be reparametrized by a one-dimensional translation in the domain. After modding out by these reparametrizations, the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
is zero-dimensional — that is, a collection of oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
points representing unparametrized flow lines.
A chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
 may then be defined as follows. The set of chains is the Z
may then be defined as follows. The set of chains is the ZInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
generated by the critical points. The differential d of the complex sends a critical point p of index i to a sum of index-(i − 1) critical points, with coefficients corresponding to the (signed) number of unparametrized flow lines from p to those index-(i − 1) critical points.
The fact that this defines a complex (that is, that d2 = 0) follows from an understanding of how the moduli spaces of gradient flows compactify
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
. Namely, in d2 p the coefficient of an index-(i − 2) critical point q is the (signed) number of broken flows consisting of an index-1 flow from p to some critical point r of index i − 1 and another index-1 flow from r to q. These broken flows exactly constitute the boundary of the moduli space of index-2 flows: The limit of any sequence of unbroken index-2 flows can be shown to be of this form, and all such broken flows arise as limits of unbroken index-2 flows. Unparametrized index-2 flows come in one-dimensional families, which compactify to compact one-manifolds. The fact that the boundary of a compact one-manifold is always zero proves that d2 p = 0.
Invariance of Morse homology
It can be shown that the homology of this complex is independent of the Morse-Smale pair (f, g) used to define it. A homotopy of pairs (ft, gt) that interpolates between any two given pairs (f0, g0) and (f1, g1) may always be defined. Either through bifurcationBifurcation
Bifurcation means the splitting of a main body into two parts.Bifurcation or Bifurcated may refer to:*Bifurcation , the division of issues in a trial for example the division of a page into two parts....
analysis or by using a continuation map
Continuation map
In differential topology, given a family of Morse-Smale functions on a smooth manifold X parameterized by a closed interval I, one can construct a Morse-Smale vector field on X × I whose critical points occur only on the boundary. The Morse differential defines a chain map from the Morse...
to define a chain map from
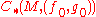 to
to 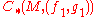 , it can be shown that the two Morse homologies are isomorphic. Analogous arguments using a homotopy of homotopies shows that this isomorphism is canonical.
, it can be shown that the two Morse homologies are isomorphic. Analogous arguments using a homotopy of homotopies shows that this isomorphism is canonical.Another approach to proving the invariance of Morse homology is to relate it directly to singular homology. One can define a map to singular homology by sending a critical point to the singular chain associated to the unstable manifold associated to that point; inversely, a singular chain is sent to the limiting critical points reached by flowing the chain using the gradient vector field. The cleanest way to do this rigorously is to use the theory of currents
Current (mathematics)
In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
.
The isomorphism with singular homology can also be proved by demonstrating an isomorphism with cellular homology
Cellular homology
In mathematics, cellular homology in algebraic topology is a homology theory for CW-complexes. It agrees with singular homology, and can provide an effective means of computing homology modules.- Definition :...
, by viewing an unstable manifold associated to a critical point of index i as an i-cell, and showing that the boundary maps in the Morse and cellular complexes correspond.
Related constructions
This approach to Morse theory was known in some form to René ThomRené Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
and Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
. It is also implicit in John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
's book on the h-cobordism
H-cobordism
A cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
theorem.
From the fact that the Morse homology is isomorphic to the singular homology, the Morse inequalities follow by considering the number of generators — that is, critical points — necessary to generate the homology groups of the appropriate ranks (and by considering truncations of the Morse complex, to get the stronger inequalities). The existence of Morse homology "explains", in the sense of categorification
Categorification
In mathematics, categorification refers to the process of replacing set-theoretic theorems by category-theoretic analogues. Categorification, when done successfully, replaces sets by categories, functions with functors, and equations by natural isomorphisms of functors satisfying additional...
, the Morse inequalities.
Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
came up with a related construction in the early 1980s sometimes known as Morse-Witten theory.
Morse homology can be extended to finite dimensional non-compact or infinite-dimensional manifolds where the index remains finite, the metric is complete and the function satisfies the Palais-Smale condition, such as the energy functional for geodesics on a Riemannian manifold. The generalization to situations in which both index and coindex are infinite, but the relative index of any pair of critical points is finite, is known as Floer homology
Floer homology
Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...
.
Sergei Novikov generalized this construction to a homology theory associated to a closed
Closed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
one-form
One-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
on a manifold. Morse homology is a special case for the one-form df. A special case of Novikov's theory is circle-valued Morse theory
Circle-valued Morse theory
In mathematics, circle-valued Morse theory studies the topology of a smooth manifold by analyzing the critical points of smooth maps from the manifold to the circle, in the framework of Morse homology...
, which Michael Hutchings and Yi-Jen Lee have connected to Reidemeister torsion and Seiberg-Witten theory.
Morse-Bott homology
Morse homology can be carried out in the Morse-Bott setting, i.e. when instead of isolated nondegenerate critical points, a function has critical manifolds whose tangent space at a point coincides with the kernel of the Hessian at the point. This situation will always occur, if the function considered is invariant w.r.t a non-discrete Lie group.To describe the resulting chain complex and its homology, introduce a generic Morse function on each critical submanifold. Chains will consist of paths that begin in a critical manifold at a critical point of the auxiliary Morse function, following a gradient trajectory with respect to some metric, and then leave the submanifold to follow the gradient vector field of the Morse-Bott function until it hits some other critical manifold; it either flows for a while along a gradient trajectory associated to the Morse function on that critical submanifold and then flows to another critical submanifold, etc., or flows to a critical point in the original submanifold and terminates. See (Frauenfelder). This approach to Morse-Bott homology appeared in the context of contact homology in (Bourgeois), in which the critical submanifolds are the sets of Reeb orbits, and the gradient flows between the critical submanifolds are pseudoholomorphic curves in the symplectization of a contact manifold asymptotic to Reeb orbits in the relevant critical manifolds of Reeb orbits.
If we extend each Morse function to a function on the entire manifold supported near the critical submanifolds, we can explicitly write down a Morse-Smale function that perturbs the original Morse-Bott function. Namely, multiply each of the extended functions by some small positive constant, sum them and add the result to the original Morse-Bott function. The broken flows described above will be C0 close to the flow lines of this Morse-Smale function.

