
Modulus (algebraic number theory)
Encyclopedia
In mathematics
, in the field of algebraic number theory
, a modulus (plural moduli) (or cycle, or extended ideal) is a formal product of places of a global field
(i.e. an algebraic number field
or a global function field). It is used to encode ramification
data for abelian extension
s of a global field.
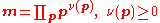
where p runs over all places of K, finite or infinite, the exponents ν(p) are zero except for finitely many p. If K is a number field, ν(p) = 0 or 1 for real places and ν(p) = 0 for complex places. If K is a function field, ν(p) = 0 for all infinite places.
In the function field case, a modulus is the same thing as an effective divisor, and in the number field case, a modulus can be considered as an Arakelov divisor.
The notion of congruence
can be extended to the setting of moduli. If a and b are elements of K×, the definition of a ≡∗b (mod pν) depends on what type of prime p is:
Then, given a modulus m, a ≡∗b (mod m) if a ≡∗b (mod pν(p)) for all p such that ν(p) > 0.
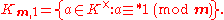
A modulus m can be split into two parts, mf and m∞, the product over the finite and infinite places, respectively. Let Im to be one of the following:
In both case, there is a group homomorphism
i : Km,1 → Im obtained by sending a to the principal ideal
(resp. divisor) (a).
The ray class group modulo m is the quotient Cm = Im / i(Km,1). A coset of i(Km,1) is called a ray class modulo m.
Erich Hecke
's original definition of Hecke character
s may be interpreted in terms of character
s of the ray class group with respect to some modulus m.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, a modulus (plural moduli) (or cycle, or extended ideal) is a formal product of places of a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
(i.e. an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
or a global function field). It is used to encode ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
data for abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
s of a global field.
Definition
Let K be a global field with ring of integers R. A modulus is a formal product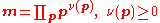
where p runs over all places of K, finite or infinite, the exponents ν(p) are zero except for finitely many p. If K is a number field, ν(p) = 0 or 1 for real places and ν(p) = 0 for complex places. If K is a function field, ν(p) = 0 for all infinite places.
In the function field case, a modulus is the same thing as an effective divisor, and in the number field case, a modulus can be considered as an Arakelov divisor.
The notion of congruence
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
can be extended to the setting of moduli. If a and b are elements of K×, the definition of a ≡∗b (mod pν) depends on what type of prime p is:
- if it is finite, then
-
- where ordp is the normalized valuation associated to p;
- if it is a real place (of a number field), then
- under the real embedding associated to p.
- if it is any other infinite place, there is no condition.
Then, given a modulus m, a ≡∗b (mod m) if a ≡∗b (mod pν(p)) for all p such that ν(p) > 0.
Ray class group
The ray modulo m is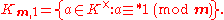
A modulus m can be split into two parts, mf and m∞, the product over the finite and infinite places, respectively. Let Im to be one of the following:
- if K is a number field, the subgroup of the group of fractional ideals generated by ideals coprime to mf;
- if K is a function field of an algebraic curveAlgebraic curveIn algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
over k, the group of divisors, rational over k, with support away from m.
In both case, there is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
i : Km,1 → Im obtained by sending a to the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
(resp. divisor) (a).
The ray class group modulo m is the quotient Cm = Im / i(Km,1). A coset of i(Km,1) is called a ray class modulo m.
Erich Hecke
Erich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
's original definition of Hecke character
Hecke character
In number theory, a Hecke character is a generalisation of a Dirichlet character, introduced by Erich Hecke to construct a class ofL-functions larger than Dirichlet L-functions, and a natural setting for the Dedekind zeta-functions and certain others which have functional equations analogous to...
s may be interpreted in terms of character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
s of the ray class group with respect to some modulus m.
Properties
When K is a number field, the following properties hold.- When m = 1, the ray class group is just the ideal class groupIdeal class groupIn mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
. - The ray class group is finite. Its order is the ray class number.
- The ray class number is divisible by the class number of K.



