
Mittag-Leffler's theorem
Encyclopedia
In complex analysis
, Mittag-Leffler's theorem concerns the existence of meromorphic function
s with prescribed poles. It is sister to the Weierstrass factorization theorem
, which asserts existence of holomorphic function
s with prescribed zeros
. It is named after Gösta Mittag-Leffler.
 be an open set
be an open set
in and
and 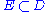 a closed
a closed
discrete subset. For each in
in  , let
, let 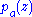 be a polynomial in
be a polynomial in 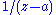 . There is a meromorphic function
. There is a meromorphic function 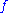 on
on  such that for each
such that for each 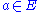 ,
, 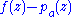 is holomorphic at
is holomorphic at  . In particular, the principal part of
. In particular, the principal part of 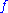 at
at  is
is  .
.
One possible method of proof is as follows. Notice that if is finite, it suffices to take
is finite, it suffices to take 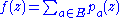 . If
. If  is not finite, consider the finite sum
is not finite, consider the finite sum 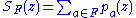 where
where  is a finite subset of
is a finite subset of  . Use Runge's theorem
. Use Runge's theorem
to construct a rational function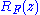 approximating
approximating 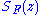 . As
. As  is exhausted by the finite sets
is exhausted by the finite sets 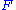 , the approximations
, the approximations 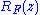 will approach a limit, which is the desired meromorphic function
will approach a limit, which is the desired meromorphic function 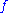 .
.
1 at all positive integers. With notation as above, letting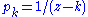 and
and 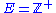 , Mittag-Leffler's theorem asserts (non-constructively) the existence of a meromorphic function
, Mittag-Leffler's theorem asserts (non-constructively) the existence of a meromorphic function 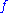 with principal part
with principal part 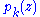 at
at  for each positive integer
for each positive integer 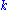 . This
. This  has the desired properties. More constructively we can let
has the desired properties. More constructively we can let 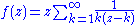 . This series converges normally
. This series converges normally
on (as can be shown using the M-test) to a meromorphic function with the desired properties.
(as can be shown using the M-test) to a meromorphic function with the desired properties.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, Mittag-Leffler's theorem concerns the existence of meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s with prescribed poles. It is sister to the Weierstrass factorization theorem
Weierstrass factorization theorem
In mathematics, the Weierstrass factorization theorem in complex analysis, named after Karl Weierstrass, asserts that entire functions can be represented by a product involving their zeroes...
, which asserts existence of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s with prescribed zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
. It is named after Gösta Mittag-Leffler.
Theorem
Let be an open set
be an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in
 and
and 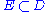 a closed
a closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
discrete subset. For each
 in
in  , let
, let 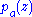 be a polynomial in
be a polynomial in 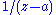 . There is a meromorphic function
. There is a meromorphic function 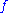 on
on  such that for each
such that for each 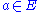 ,
, 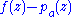 is holomorphic at
is holomorphic at  . In particular, the principal part of
. In particular, the principal part of 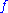 at
at  is
is  .
.One possible method of proof is as follows. Notice that if
 is finite, it suffices to take
is finite, it suffices to take 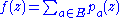 . If
. If  is not finite, consider the finite sum
is not finite, consider the finite sum 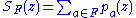 where
where  is a finite subset of
is a finite subset of  . Use Runge's theorem
. Use Runge's theoremRunge's theorem
In complex analysis, Runge's theorem, also known as Runge's approximation theorem, named after the German Mathematician Carl Runge, and put forward by him in the year 1885, states the following: If K is a compact subset of C , A is a set containing at least one complex number from every bounded...
to construct a rational function
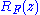 approximating
approximating 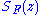 . As
. As  is exhausted by the finite sets
is exhausted by the finite sets 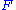 , the approximations
, the approximations 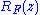 will approach a limit, which is the desired meromorphic function
will approach a limit, which is the desired meromorphic function 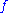 .
.Example
Suppose that we desire a meromorphic function with simple poles of residueResidue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
1 at all positive integers. With notation as above, letting
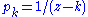 and
and 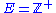 , Mittag-Leffler's theorem asserts (non-constructively) the existence of a meromorphic function
, Mittag-Leffler's theorem asserts (non-constructively) the existence of a meromorphic function 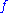 with principal part
with principal part 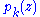 at
at  for each positive integer
for each positive integer 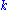 . This
. This  has the desired properties. More constructively we can let
has the desired properties. More constructively we can let 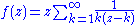 . This series converges normally
. This series converges normallyNormal convergence
In mathematics normal convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved when the order of summation is changed.- History :...
on
 (as can be shown using the M-test) to a meromorphic function with the desired properties.
(as can be shown using the M-test) to a meromorphic function with the desired properties.

