
Malgrange preparation theorem
Encyclopedia
In mathematics, the Malgrange preparation theorem is an analogue of the Weierstrass preparation theorem
for smooth functions. It was conjectured by René Thom
and proved by .
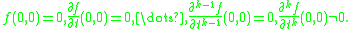
Then one form of the preparation theorem states that near the origin f can be written as the product of a smooth function c that is nonzero at the origin and a smooth function that as a function of t is a polynomial of degree k. In other words,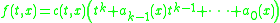
where the functions c and a are smooth and c is nonzero at the origin.
A second form of the theorem, occasionally called the Mather division theorem, is a sort of "division with remainder" theorem: it says that if f and k satisfy the conditions above and g is a smooth function near the origin, then we can write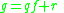
where q and r are smooth, and as a function of t, r is a polynomial of degree less than k. This means that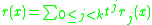
for some smooth functions rj(x).
The two forms of the theorem easily imply each other: the first form is the special case of the "division with remainder" form where g is tk, and the division with remainder form follows from the first form of the theorem as we may assume that f as a function of t is a polynomial of degree k.
If the functions f and g are real, then the functions c, a, q, and r can also be taken to be real. In the case of the Weierstrass preparation theorem these functions are uniquely determined by f and g, but uniqueness no longer holds for the Malgrange preparation theorem.
For a proof along these lines see or
over rings
of smooth, real-valued germs
. If X is a manifold
, with p∈X, let C∞p(X) denote the ring of real-valued germs of smooth functions at p on X. Let Mp(X) denote the unique maximal ideal
of C∞p(X), consisting of germs which vanish at p. Let A be a C∞p(X)-module, and let f:X → Y be a smooth function between manifolds. Let q = f(p). f induces a ring homomorphism f*:C∞q(Y) → C∞p(X) by composition on the right with f. Thus we can view A as a C∞q(Y)-module. Then the Malgrange preparation theorem says that if A is a finitely-generated C∞p(X)-module, then A is a finitely-generated C∞q(Y)-module if and only if A/Mq(Y)A is a finite-dimensional real vector space.
Weierstrass preparation theorem
In mathematics, the Weierstrass preparation theorem is a tool for dealing with analytic functions of several complex variables, at a given point P...
for smooth functions. It was conjectured by René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
and proved by .
Statement of Malgrange preparation theorem
Suppose that f(t,x) is a smooth complex function of t∈R and x∈Rn near the origin, and let k be the smallest integer such that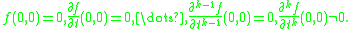
Then one form of the preparation theorem states that near the origin f can be written as the product of a smooth function c that is nonzero at the origin and a smooth function that as a function of t is a polynomial of degree k. In other words,
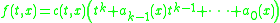
where the functions c and a are smooth and c is nonzero at the origin.
A second form of the theorem, occasionally called the Mather division theorem, is a sort of "division with remainder" theorem: it says that if f and k satisfy the conditions above and g is a smooth function near the origin, then we can write
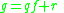
where q and r are smooth, and as a function of t, r is a polynomial of degree less than k. This means that
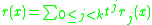
for some smooth functions rj(x).
The two forms of the theorem easily imply each other: the first form is the special case of the "division with remainder" form where g is tk, and the division with remainder form follows from the first form of the theorem as we may assume that f as a function of t is a polynomial of degree k.
If the functions f and g are real, then the functions c, a, q, and r can also be taken to be real. In the case of the Weierstrass preparation theorem these functions are uniquely determined by f and g, but uniqueness no longer holds for the Malgrange preparation theorem.
Proof of Malgrange preparation theorem
The Malgrange preparation theorem can be deduced from the Weierstrass preparation theorem. The obvious way of doing this does not work: although smooth functions have a formal power series expansion at the origin, and the Weierstrass preparation theorem applies to formal power series, the formal power series will not usually converge to smooth functions near the origin. Instead one can use the idea of decomposing a smooth function as a sum of analytic functions by applying a partition of unity to its Fourier transform.For a proof along these lines see or
Algebraic version of the Malgrange preparation theorem
The Malgrange preparation theorem can be restated as a theorem about modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of smooth, real-valued germs
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
. If X is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, with p∈X, let C∞p(X) denote the ring of real-valued germs of smooth functions at p on X. Let Mp(X) denote the unique maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
of C∞p(X), consisting of germs which vanish at p. Let A be a C∞p(X)-module, and let f:X → Y be a smooth function between manifolds. Let q = f(p). f induces a ring homomorphism f*:C∞q(Y) → C∞p(X) by composition on the right with f. Thus we can view A as a C∞q(Y)-module. Then the Malgrange preparation theorem says that if A is a finitely-generated C∞p(X)-module, then A is a finitely-generated C∞q(Y)-module if and only if A/Mq(Y)A is a finite-dimensional real vector space.

