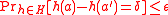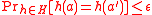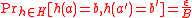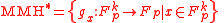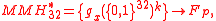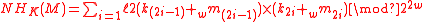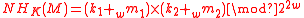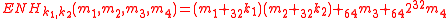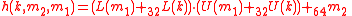MMH-Badger MAC
Encyclopedia
In cryptography
, to guarantee the integrity of a message, one can use either public key digital signatures or use a Message Authentication Code
(MAC). A MAC is one of the possible authentication
techniques involving the use of a secret key to generate a small fixed-size block of data. The basic setting of MAC is as follows. Two parties A and B want to communicate by sending a message . They share a secret key
. They share a secret key  . When A sends a message to B then A calculates the MAC as a function of the message and the key
. When A sends a message to B then A calculates the MAC as a function of the message and the key  . The message and the key are sent to B. Then B uses the same secret key
. The message and the key are sent to B. Then B uses the same secret key  and calculates the MAC on the received message. The received MAC is compared to the new MAC. When it matches then the message is authentic because only the receiver and the sender know the secret key.
and calculates the MAC on the received message. The received MAC is compared to the new MAC. When it matches then the message is authentic because only the receiver and the sender know the secret key.
to construct a message authentication code
s (MACs). Universal hashing
is used to build secure message authentication schemes where the opponent’s ability to fake messages is bounded by the collision probability of the hash family. Proposals such as UMAC
, CRC32, BOB, Poly1305-AES
, and IPSX deal with implementation of universal hashing
as a tool for achieving fast and secure message authentication
. This page discusses MMH and Badger.
was first introduced by Carter and Wegman in 1979 and was studied further by Sarwate, Wegman and Carter and Stinson. Universal hashing
has many important applications in theoretical computer science
and was used by Wegman and Carter in the construction of message authentication codes (MACs) in. Universal hashing
can be defined as a mapping from a finite set A with size a to a finite set B with size b.
The following sections define properties a universal hash function should satisfy.
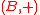 be an Abelian group
be an Abelian group
. A family H of hash functions that maps from a set A to B is said to be ϵ-almost ∆-universal (ϵ-A∆U) w.r.t.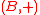 , if for any distinct elements
, if for any distinct elements 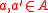 and for all
and for all  :
:
H is ∆-universal (∆U) if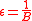 .
.
Let ϵ be any positive real number. An ϵ-almost universal (ϵ-AU) family H of hash functions mapping from a set A to B is a family of functions from A to B, such that for any distinct elements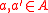 :
:
H is universal (U) if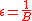 .
.
The definition above states that the probability of a collision is at most ϵ for any two distinct inputs.
Let ϵ be any positive real number. An ϵ-almost strongly-universal (ϵ-ASU) family H of Hash functions maps from a set A to B is a family of functions from A to B, such that for any distinct elements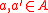 and all
and all 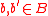 :
:
and
H is strongly universal (SU) if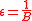 .
.
The first condition states that the probability that a given input a is mapped to a given output b equals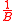 . The second condition implies that if a is mapped to b, then the conditional probability that
. The second condition implies that if a is mapped to b, then the conditional probability that  with
with  is mapped to
is mapped to 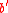 is upper bounded by ϵ.
is upper bounded by ϵ.
are for example to verify the integrity
of an on-line multimedia title. The performance of MMH is based on the improved support of integer scalar
-products in modern microprocessors.
MMH uses single precision scalar-products as its most basic operation. It consists of a (modified) inner product between the message and a key modulo
a prime
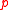 . The construction of MMH works in the finite field
. The construction of MMH works in the finite field
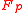 for some prime integer
for some prime integer 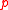 .
.
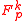 for some positive integer
for some positive integer  . The family MMH* of functions from
. The family MMH* of functions from 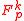 to
to 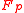 is defined as follows.
is defined as follows.
where x, m are vectors, and the functions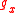 are defined as follows.
are defined as follows.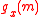 =
=  =
= 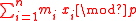
In the case of MAC, is a message and
is a message and  is a key where
is a key where 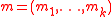 and
and 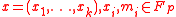 .
.
MMH* should satisfy the security requirements of a MAC, enabling say Ana and Bob to communicate in an authenticated way. They have a secret key . Say Charles listens to the conversation between Ana and Bob and wants to change the message into his own message to Bob which should pass as a message from Ana. So, his message
. Say Charles listens to the conversation between Ana and Bob and wants to change the message into his own message to Bob which should pass as a message from Ana. So, his message  and Ana's message
and Ana's message  will differ in at least one bit (eg.
will differ in at least one bit (eg. 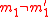 ).
).
Assume that Charles knows that the function is of the form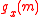 and he knows Ana's message
and he knows Ana's message  but he does not know the key x then the probability that Charles can change the message or send his own message can be explained by the following theorem.
but he does not know the key x then the probability that Charles can change the message or send his own message can be explained by the following theorem.
Theorem 1:The family MMH* is ∆-universal.
Proof:
Take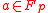 , and let
, and let 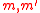 be two different messages. Assume without loss of generality
be two different messages. Assume without loss of generality
that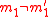 . Then for any choice of
. Then for any choice of  , there is
, there is
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, to guarantee the integrity of a message, one can use either public key digital signatures or use a Message Authentication Code
Message authentication code
In cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...
(MAC). A MAC is one of the possible authentication
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
techniques involving the use of a secret key to generate a small fixed-size block of data. The basic setting of MAC is as follows. Two parties A and B want to communicate by sending a message
 . They share a secret key
. They share a secret key  . When A sends a message to B then A calculates the MAC as a function of the message and the key
. When A sends a message to B then A calculates the MAC as a function of the message and the key  . The message and the key are sent to B. Then B uses the same secret key
. The message and the key are sent to B. Then B uses the same secret key  and calculates the MAC on the received message. The received MAC is compared to the new MAC. When it matches then the message is authentic because only the receiver and the sender know the secret key.
and calculates the MAC on the received message. The received MAC is compared to the new MAC. When it matches then the message is authentic because only the receiver and the sender know the secret key.Introduction
Carter and Wegman introduced universal hashingUniversal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
to construct a message authentication code
Message authentication code
In cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...
s (MACs). Universal hashing
Universal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
is used to build secure message authentication schemes where the opponent’s ability to fake messages is bounded by the collision probability of the hash family. Proposals such as UMAC
UMAC
In cryptography, a message authentication code based on universal hashing, or UMAC, is a type of message authentication code calculated choosing a hash function from a class of hash functions according to some secret process and applying it to the message. The resulting digest or fingerprint is...
, CRC32, BOB, Poly1305-AES
Poly1305-AES
Poly1305-AES is a cryptographic message authentication code written by Daniel J. Bernstein. It can be used to verify the data integrity and the authenticity of a message.-Description:...
, and IPSX deal with implementation of universal hashing
Universal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
as a tool for achieving fast and secure message authentication
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
. This page discusses MMH and Badger.
Universal hash function families
Universal hashingUniversal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
was first introduced by Carter and Wegman in 1979 and was studied further by Sarwate, Wegman and Carter and Stinson. Universal hashing
Universal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
has many important applications in theoretical computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and was used by Wegman and Carter in the construction of message authentication codes (MACs) in. Universal hashing
Universal hashing
Using universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
can be defined as a mapping from a finite set A with size a to a finite set B with size b.
The following sections define properties a universal hash function should satisfy.
ϵ-almost ∆-universal (ϵ-A∆U)
Let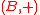 be an Abelian group
be an Abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. A family H of hash functions that maps from a set A to B is said to be ϵ-almost ∆-universal (ϵ-A∆U) w.r.t.
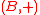 , if for any distinct elements
, if for any distinct elements 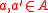 and for all
and for all  :
:H is ∆-universal (∆U) if
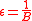 .
.ϵ-almost universal family or (ϵ-AU) family
An ϵ-almost universal family or (ϵ-AU) family is one type of family in the universal hash function. This property is defined as follows:Let ϵ be any positive real number. An ϵ-almost universal (ϵ-AU) family H of hash functions mapping from a set A to B is a family of functions from A to B, such that for any distinct elements
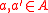 :
:H is universal (U) if
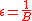 .
.The definition above states that the probability of a collision is at most ϵ for any two distinct inputs.
ϵ-almost strongly-universal family or (ϵ-ASU)family
An ϵ-almost strongly universal family or (ϵ-ASU)family is one type of family in the universal hash function defined as follows:Let ϵ be any positive real number. An ϵ-almost strongly-universal (ϵ-ASU) family H of Hash functions maps from a set A to B is a family of functions from A to B, such that for any distinct elements
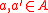 and all
and all 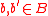 :
:and
H is strongly universal (SU) if
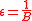 .
.The first condition states that the probability that a given input a is mapped to a given output b equals
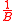 . The second condition implies that if a is mapped to b, then the conditional probability that
. The second condition implies that if a is mapped to b, then the conditional probability that  with
with  is mapped to
is mapped to 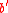 is upper bounded by ϵ.
is upper bounded by ϵ.MMH (Multilinear Modular Hashing)
The name MMH stands for Multilinear-Modular-Hashing. Applications in MultimediaMultimedia
Multimedia is media and content that uses a combination of different content forms. The term can be used as a noun or as an adjective describing a medium as having multiple content forms. The term is used in contrast to media which use only rudimentary computer display such as text-only, or...
are for example to verify the integrity
Integrity
Integrity is a concept of consistency of actions, values, methods, measures, principles, expectations, and outcomes. In ethics, integrity is regarded as the honesty and truthfulness or accuracy of one's actions...
of an on-line multimedia title. The performance of MMH is based on the improved support of integer scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
-products in modern microprocessors.
MMH uses single precision scalar-products as its most basic operation. It consists of a (modified) inner product between the message and a key modulo
Modulo
In the mathematical community, the word modulo is often used informally. Generally, to say "A is the same as B modulo C" means, more-or-less, "A and B are the same except for differences accounted for or explained by C"....
a prime
Prime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
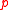 . The construction of MMH works in the finite field
. The construction of MMH works in the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
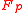 for some prime integer
for some prime integer 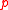 .
.MMH*
MMH* involves a construction of a family of hash functions consisting of multilinear functions on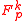 for some positive integer
for some positive integer  . The family MMH* of functions from
. The family MMH* of functions from 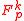 to
to 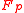 is defined as follows.
is defined as follows.where x, m are vectors, and the functions
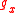 are defined as follows.
are defined as follows.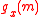 =
=  =
= 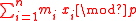
In the case of MAC,
 is a message and
is a message and  is a key where
is a key where 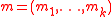 and
and 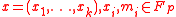 .
.MMH* should satisfy the security requirements of a MAC, enabling say Ana and Bob to communicate in an authenticated way. They have a secret key
 . Say Charles listens to the conversation between Ana and Bob and wants to change the message into his own message to Bob which should pass as a message from Ana. So, his message
. Say Charles listens to the conversation between Ana and Bob and wants to change the message into his own message to Bob which should pass as a message from Ana. So, his message  and Ana's message
and Ana's message  will differ in at least one bit (eg.
will differ in at least one bit (eg. 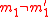 ).
).Assume that Charles knows that the function is of the form
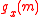 and he knows Ana's message
and he knows Ana's message  but he does not know the key x then the probability that Charles can change the message or send his own message can be explained by the following theorem.
but he does not know the key x then the probability that Charles can change the message or send his own message can be explained by the following theorem.Theorem 1:The family MMH* is ∆-universal.
Proof:
Take
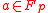 , and let
, and let 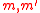 be two different messages. Assume without loss of generality
be two different messages. Assume without loss of generalityWithout loss of generality
Without loss of generality is a frequently used expression in mathematics...
that
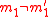 . Then for any choice of
. Then for any choice of  , there is
, there is
-
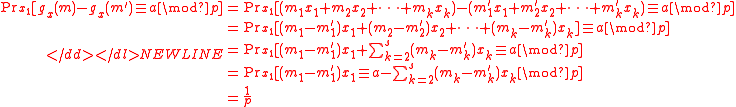
To explain the theorem above, take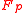 for
for 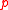 prime represent the field as
prime represent the field as 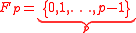 . If one takes an element in
. If one takes an element in 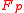 , let say
, let say 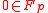 then the probability that
then the probability that 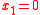 is
is
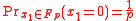
So, what one actually needs to compute is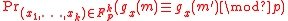
But,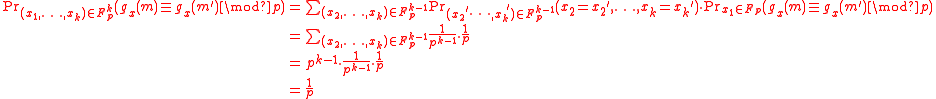
From the proof above, is the collision probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is the collision probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of the attacker in 1 round, so on average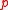 verification queries will suffice to get one message accepted. To reduce the collisionCollisionA collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
verification queries will suffice to get one message accepted. To reduce the collisionCollisionA collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, it is necessary to choose large p or to concatenate such MACs using
such MACs using  independent keys so that the collisionCollisionA collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
independent keys so that the collisionCollisionA collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
becomes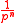 . In this case the number of keys are increased by a factor of
. In this case the number of keys are increased by a factor of  and the output is also increased by
and the output is also increased by  .
.
Halevi and Krawczyk construct a variant called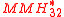
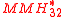 . The construction works with 32-bit integers and with the primePrimeA prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
. The construction works with 32-bit integers and with the primePrimeA prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
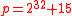 . Actually the primePrimeA prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
. Actually the primePrimeA prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
p can be chosen to be any prime which satisfies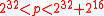 . This idea is adopted from the suggestion by Carter and Wegman to use the primes
. This idea is adopted from the suggestion by Carter and Wegman to use the primes  or
or 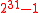 .
.
-
 is defined as follows:
is defined as follows:
where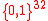 means
means 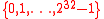 (i.e., binary representation)
(i.e., binary representation)
The functions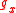 are defined as follows.
are defined as follows.
-
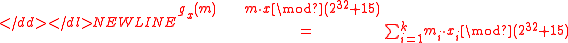
where
-
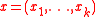 ,
, 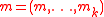
By theorem 1, the collisionCollisionA collision is an isolated event which two or more moving bodies exert forces on each other for a relatively short time.Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies...
probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is about ϵ = , and the family of
, and the family of 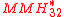 can be defined as ϵ-almost ∆ Universal with ϵ =
can be defined as ϵ-almost ∆ Universal with ϵ =  .
.
The value of k
The value of k that describes the length of the message and key vectorsTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
has several effects:- Since the costly modular reduction over k is multiply and add operations increasing k should decrease the speed.
- Since the key x consist of k 32-bit integers increasing k will results in a longer key.
- The probability of breaking the system is
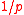 and
and 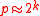 so increasing k makes the system harder to break.
so increasing k makes the system harder to break.
Performance
Below are the timing results for various implementations of MMH in 1997, designed by Halevi and Krawczyk.- A 150 Mhz PowerPCPowerPCPowerPC is a RISC architecture created by the 1991 Apple–IBM–Motorola alliance, known as AIM...
604 RISC machine running AIX150 MHz PowerPC PowerPCPowerPC is a RISC architecture created by the 1991 Apple–IBM–Motorola alliance, known as AIM...
604Message in Memory Message in Cache 64-bit 390 Mbit/second 417 Mbit/second 32-bit output 597 Mbit/second 820 Mbit/second
- A 150 MHz Pentium-Pro machine running Windows NTWindows NTWindows NT is a family of operating systems produced by Microsoft, the first version of which was released in July 1993. It was a powerful high-level-language-based, processor-independent, multiprocessing, multiuser operating system with features comparable to Unix. It was intended to complement...
150 MHz PowerPC 604 Message in Memory Message in Cache 64-bit 296 Mbit/second 356 Mbit/second 32-bit output 556 Mbit/second 813 Mbit/second
- A 200 MHz Pentium-Pro machine running LinuxLinuxLinux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...
150 MHz PowerPC 604 Message in Memory Message in Cache 64-bit 380 Mbit/second 500 Mbit/second 32-bit output 645 Mbit/second 1080 Mbit/second
Badger
Badger is a Message Authentication CodeMessage authentication codeIn cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...
(MAC) based on the idea of universal hashingUniversal hashingUsing universal hashing refers to selecting a hash function at random from a family of hash functions with a certain mathematical property . This guarantees a low number of collisions in expectation, even if the data is chosen by an adversary...
and was developed by Boesgaard, Christensen, and Zenner. It is constructed by strengthening the ∆-universal hash family MMH using an ϵ-almost strongly universal (ASU) hash function family after the application of ENH (see below), where the value of ϵ is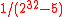 . Since Badger is a MAC function based on the universal hash function approach, the conditions needed for the security of Badger are the same as those for other universal hash functions such as UMACUMACIn cryptography, a message authentication code based on universal hashing, or UMAC, is a type of message authentication code calculated choosing a hash function from a class of hash functions according to some secret process and applying it to the message. The resulting digest or fingerprint is...
. Since Badger is a MAC function based on the universal hash function approach, the conditions needed for the security of Badger are the same as those for other universal hash functions such as UMACUMACIn cryptography, a message authentication code based on universal hashing, or UMAC, is a type of message authentication code calculated choosing a hash function from a class of hash functions according to some secret process and applying it to the message. The resulting digest or fingerprint is...
.
The Badger MAC processes a message of length up to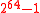 bits and returns an authenticationAuthenticationAuthentication is the act of confirming the truth of an attribute of a datum or entity...
bits and returns an authenticationAuthenticationAuthentication is the act of confirming the truth of an attribute of a datum or entity...
tagTag (metadata)In online computer systems terminology, a tag is a non-hierarchical keyword or term assigned to a piece of information . This kind of metadata helps describe an item and allows it to be found again by browsing or searching...
of length bits, where
bits, where  . According to the securitySecuritySecurity is the degree of protection against danger, damage, loss, and crime. Security as a form of protection are structures and processes that provide or improve security as a condition. The Institute for Security and Open Methodologies in the OSSTMM 3 defines security as "a form of protection...
. According to the securitySecuritySecurity is the degree of protection against danger, damage, loss, and crime. Security as a form of protection are structures and processes that provide or improve security as a condition. The Institute for Security and Open Methodologies in the OSSTMM 3 defines security as "a form of protection...
needs, user can choose the value of , that is the number of parallel hash treeHash treeIn cryptography and computer science Hash trees or Merkle trees are a type of data structure which contains a tree of summary information about a larger piece of data – for instance a file – used to verify its contents. Hash trees are a combination of hash lists and hash chaining, which in turn are...
, that is the number of parallel hash treeHash treeIn cryptography and computer science Hash trees or Merkle trees are a type of data structure which contains a tree of summary information about a larger piece of data – for instance a file – used to verify its contents. Hash trees are a combination of hash lists and hash chaining, which in turn are...
s in Badger. One can choose larger values of u, but those values do not influence further the security of MAC. The algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
uses a 128-bit key and the limited message length to be processed under this key is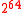 .
.
The key setup has to be run only once per key in order to run the Badger algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
under a given key, since the resulting internal state of the MAC can be saved to be used with any other message that will be processed later.
ENH
Hash families can be combined in order to obtain new hash families. For the ϵ-AU, ϵ-A∆U, and ϵ-ASU families, the latter are contained in the former. For instance, an A∆U family is also an AU family, an ASU is also an A∆U family, and so forth. On the other hand, a stronger family can be reduced to a weaker one, as long as a performance gain can be reached. A method to reduce ∆-universal hash function to universal hash functions will be described in the following.
Theorem 2
Let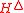 be an ϵ-AΔU hash family from a set A to a set B. Consider a message
be an ϵ-AΔU hash family from a set A to a set B. Consider a message 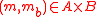 . Then the family H consisting of the functions
. Then the family H consisting of the functions 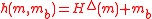 is ϵ-AU.
is ϵ-AU.
If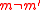 , then the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, then the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that
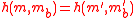 is at most ϵ,
is at most ϵ,
since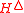 is an ϵ-A∆U family. If
is an ϵ-A∆U family. If 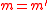 but
but 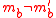 , then the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, then the probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is trivially 0.
The proof for Theorem 2 was described in
The ENH-family is constructed based on the universal hash family NH (which is also used in UMACUMACIn cryptography, a message authentication code based on universal hashing, or UMAC, is a type of message authentication code calculated choosing a hash function from a class of hash functions according to some secret process and applying it to the message. The resulting digest or fingerprint is...
):
Where ‘ ’ means ‘addition modulo
’ means ‘addition modulo 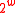 ’, and
’, and  . It is a
. It is a 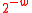 -A∆U hash family.
-A∆U hash family.
Lemma 1
The following version of NH is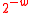 -A∆U:
-A∆U:
Choosing w=32 and applying Theorem 1, one can obtain the -AU function family ENH, which will be the basic building block of the badger MAC:
-AU function family ENH, which will be the basic building block of the badger MAC:
where all arguments are 32-bits long and the output has 64-bits.
Construction
Badger is constructed using the strongly universality hash family and can be described as
where an -AU universal function family H* is used to hash messages of any size onto a fixed size and an
-AU universal function family H* is used to hash messages of any size onto a fixed size and an 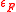 -ASU function family F is used to guarantee the strong universality of the overall construction. NH and ENH are used to construct H*. The maximum input size of the function family H* is
-ASU function family F is used to guarantee the strong universality of the overall construction. NH and ENH are used to construct H*. The maximum input size of the function family H* is 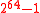 and the output size is 128 bits, split into 64 bits each for the message and the hash. The collsion probability for the H*-function ranges from
and the output size is 128 bits, split into 64 bits each for the message and the hash. The collsion probability for the H*-function ranges from  to
to 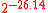 . To construct the strongly universal function family F, the ∆-universal hash family MMH* is transformed into a strongly universal hash family by adding an additional key.
. To construct the strongly universal function family F, the ∆-universal hash family MMH* is transformed into a strongly universal hash family by adding an additional key.
Two steps on Badger
There are two steps that have to be executed for every message: processing phase and finalize phase.
Processing phase
In this phase, the data is hashed to a 64-bit string. A core function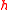 :
: 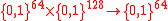 is used in this processing phase, that hashes a 128-bit string
is used in this processing phase, that hashes a 128-bit string 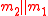 to a 64-bit string
to a 64-bit string 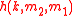 as follows:
as follows:
for any n, means addition modulo
means addition modulo 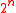 . Given a 2n-bit string x, L(x) means least significant n bits, and U(x) means most significant n bits.
. Given a 2n-bit string x, L(x) means least significant n bits, and U(x) means most significant n bits.
A message can be processed by using this function. Denote level_key [j][i] by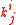 .
.
Pseudo-code of the processing phase is as follow.
L=|M|
if L=0
M^1=⋯=M^u=0
Go to finalization
r=L mod 64
if r≠0:
M=0^(64-r)∥M
for i=1 to u:
M^i=M
v^'=max{1,⌈log_2 L⌉-6}
for j=1 to v^':
divide M^i into 64-bit blocks, M^i=m_t^i∥⋯∥m_1^i
if t is even:
M^i=h(k_j^i,m_t^i,m_(t-1)^i )∥⋯∥h(k_j^i,m_2^i,m_1^i )
else
M^i=m_t^i∥h(k_j^i,m_(t-1)^i,m_(t-2)^i )∥⋯∥h(k_j^i,m_2^i,m_1^i )
Finalize phase
In this phase, the 64-string resulting from the processing phase is transformed into the desired MAC tag. This finalization phase uses the RabbitRabbit (cipher)Rabbit is a high-speed stream cipher first presented in February 2003 at the 10th FSE workshop. In May 2005, it was submitted to the eSTREAM project of the ECRYPT network....
stream cipherStream cipherIn cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
and uses both key setup and IV setup by taking the finalization key final_key[j][i] as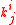 .
.
Pseudo-code of the finalization phase
RabbitKeySetup(K)
RabbitIVSetup(N)
for i=1 to u:
Q^i=0^7∥L∥M^i
divide Q^i into 27-bit blocks, Q^i=q_5^i∥⋯∥q_1^i
S^i=(∑_(j=1)^5 (q_j^i K_j^i))+K_6^i mod p
S=S^u∥⋯∥S^1
S=S ⨁ RabbitNextbit(u∙32)
return S
Notation:
From the pseudocode above, k denotes the key in the Rabbit Key Setup(K) which initializes Rabbit with the 128-bit key k. M denotes the message to be hashed and |M| denotes the length of the message in bits. q_i denotes a message M that is divided into i blocks. For the given 2n-bit string x then L(x) and U(x) respectively denoted its least significant n bits and most significant n bits.
Performance
Boesgard, Christensen and Zenner report the performance of Badger measured on a 1.0 GHz Pentium IIIPentium IIIThe Pentium III brand refers to Intel's 32-bit x86 desktop and mobile microprocessors based on the sixth-generation P6 microarchitecture introduced on February 26, 1999. The brand's initial processors were very similar to the earlier Pentium II-branded microprocessors...
and on a 1.7 Ghz Pentium 4Pentium 4Pentium 4 was a line of single-core desktop and laptop central processing units , introduced by Intel on November 20, 2000 and shipped through August 8, 2008. They had a 7th-generation x86 microarchitecture, called NetBurst, which was the company's first all-new design since the introduction of the...
processor. The speed-optimized versions were programmed in assembly language inlined in C and compiled using the Intel C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
7.1 compiler.
The following table presents Badger's properties for various restricted message lengths. “Memory req.” denotes the amount of memory required to store the internal state including key material and the inner state of the RabbitRabbit (cipher)Rabbit is a high-speed stream cipher first presented in February 2003 at the 10th FSE workshop. In May 2005, it was submitted to the eSTREAM project of the ECRYPT network....
stream cipherStream cipherIn cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
. “Setup” denotes the key setup, and “Fin.” denotes finalization with IV-setup.
Max. Message Size Forgery Bound Memory Reg. Setup Pentium III Fin. Pentium III Setup Pentium III Fin. Pentium III 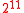 bytes (e.g.IPsec)
bytes (e.g.IPsec)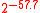
400 bytes 1133 cycles 409 cycles 1774 cycles 776 cycles 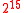 bytes (e.g.TLS)
bytes (e.g.TLS)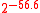
528 bytes 1370 cycles 421 cycles 2100 cycles 778 cycles 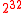 bytes
bytes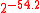
1072 bytes 2376 cycles 421 cycles 3488 cycles 778 cycles 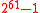 bytes
bytes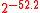
2000 bytes 4093 cycles 433 cycles 5854 cycles 800 cycles -
-