MAXEkSAT
Encyclopedia
MAXEkSAT is a problem in computational complexity theory
that is a maximization version of the Boolean satisfiability problem 3SAT
.
In MAXEkSAT, each clause has exactly k literals, with k ≥ 3, and is in conjunctive normal form
. These formulas are called kCNF formulas.
The problem is to determine the maximum number of clauses that can be satisfied by a truth assignment to the variables in the clauses.
We say that an algorithm A provides an α-approximation
to MAXEkSAT if, for some fixed positive α less than or equal to 1, and every kCNF formula φ, A can find a truth assignment to the variables of φ that will satisfy at least an α-fraction of the maximum number of satisfiable clauses of φ.
Note that since 3SAT is NP-hard
, and since any 1-approximation algorithm for MAXEkSAT could easily be converted into an algorithm for accepting the language 3SAT, 1-approximation of MAXEkSAT is NP-hard.
A natural next question is how big α can be guaranteed to be for an explicit algorithm that runs in polynomial time (P
).
One answer, relying on results in the study of error correcting codes, works for any constant k, providing a polynomial time algorithm for finding such an assignment.
We need one definition and two facts to find the algorithm.
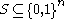is an ℓ-wise independent source if, for a uniformly chosen random (x1, x2, ..., xn) ∈ S, x1, x2, ..., xn are ℓ-wise independent
random variables.
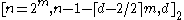linear code.
There exists an ℓ-wise independent source of size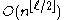
, namely the dual of a BCH2,log n,ℓ+1 code, which is a linear code. Since every BCH code
can be presented as a polynomial-time computable restriction of a related Reed Solomon code, which itself is strongly explicit, there is a polynomial-time algorithm for finding such an assignment to the xi's. The proof of fact 2 can be found at Dual of BCH is an independent source
.
To summarize, generate BCH2,log n,ℓ+1, compute its dual, which as a set is an ℓ-wise independent source, and treat each element (codeword) of that source as a truth assignment to the n variables in φ. At least one of them will satisfy at least 1 − 2−ℓ of the clauses of φ, whenever φ is in kCNF form, k = ℓ.
For ℓ = 3, this derandomizes the initially described algorithm for MAXE3SAT.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
that is a maximization version of the Boolean satisfiability problem 3SAT
3sat
3sat is the name of a public, advertising-free, television network in Central Europe. The programming is in German and is broadcast primarily within Germany, Austria and Switzerland .3sat was established for cultural...
.
In MAXEkSAT, each clause has exactly k literals, with k ≥ 3, and is in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
. These formulas are called kCNF formulas.
The problem is to determine the maximum number of clauses that can be satisfied by a truth assignment to the variables in the clauses.
We say that an algorithm A provides an α-approximation
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
to MAXEkSAT if, for some fixed positive α less than or equal to 1, and every kCNF formula φ, A can find a truth assignment to the variables of φ that will satisfy at least an α-fraction of the maximum number of satisfiable clauses of φ.
Note that since 3SAT is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, and since any 1-approximation algorithm for MAXEkSAT could easily be converted into an algorithm for accepting the language 3SAT, 1-approximation of MAXEkSAT is NP-hard.
A natural next question is how big α can be guaranteed to be for an explicit algorithm that runs in polynomial time (P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
).
Main idea
A simple result is that there is a simple randomized algorithm that provides a 7/8-approximation to MAXE3SAT which runs in polynomial time: For each i, set variable xi in formula φ to be true with probability 1/2, and false with probability 1/2.Proof
In a 3CNF formula, there are three boolean variables; consequently, the number of possible combination of assignments to the three variables is 8. Since there is only one combination of truth assignments to a clause that will render it false, we have a 7/8 probability of stumbling across a valid assignment for any given clause. Thus, the expected fraction of satisfied clauses is 7/8. Because this expectation is over all possible assignments to variables, this guarantees the existence of some assignment that satisfies at least 7/8-fraction of clauses of any 3CNF formula.Main question
But even if we know that there exists such a satisfying assignment, how would we find one? We could cycle through all 2n assignments until we found one, but clearly that approach can't be guaranteed to run in polynomial time.One answer, relying on results in the study of error correcting codes, works for any constant k, providing a polynomial time algorithm for finding such an assignment.
We need one definition and two facts to find the algorithm.
Definition
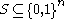is an ℓ-wise independent source if, for a uniformly chosen random (x1, x2, ..., xn) ∈ S, x1, x2, ..., xn are ℓ-wise independentPairwise independence
In probability theory, a pairwise independent collection of random variables is a set of random variables any two of which are independent. Any collection of mutually independent random variables is pairwise independent, but some pairwise independent collections are not mutually independent...
random variables.
Fact 1
Note that such an assignment can be found among elements of any ℓ-wise independent source over n binary variables. This is easier to see once you realize that an ℓ-wise independent source is really just any set of binary vectors over {0, 1}n with the property that all restrictions of those vectors to ℓ co-ordinates must present the 2ℓ possible binary combinations an equal number of times.Fact 2
Recall that BCH2,m,d is an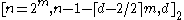 linear code.There exists an ℓ-wise independent source of size
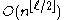, namely the dual of a BCH2,log n,ℓ+1 code, which is a linear code. Since every BCH codeBCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
can be presented as a polynomial-time computable restriction of a related Reed Solomon code, which itself is strongly explicit, there is a polynomial-time algorithm for finding such an assignment to the xi's. The proof of fact 2 can be found at Dual of BCH is an independent source
Dual of BCH is an independent source
A certain family of BCH codes have a particularly useful property, which is thattreated as linear operators, their dual operators turns their input into an \ell-wise independent source. That is, the set of vectors from the input vector space are mapped to an \ell-wise independent source...
.
To summarize, generate BCH2,log n,ℓ+1, compute its dual, which as a set is an ℓ-wise independent source, and treat each element (codeword) of that source as a truth assignment to the n variables in φ. At least one of them will satisfy at least 1 − 2−ℓ of the clauses of φ, whenever φ is in kCNF form, k = ℓ.
For ℓ = 3, this derandomizes the initially described algorithm for MAXE3SAT.