
Lefschetz manifold
Encyclopedia
In mathematics
, a Lefschetz manifold is a particular kind of symplectic manifold
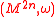 , sharing a certain cohomological property with Kaehler manifolds, that of satisfying the conclusion of the Hard Lefschetz theorem. More precisely, the strong Lefschetz property asks that for
, sharing a certain cohomological property with Kaehler manifolds, that of satisfying the conclusion of the Hard Lefschetz theorem. More precisely, the strong Lefschetz property asks that for 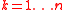 , the cup product
, the cup product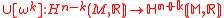
be an isomorphism.
The topology of these symplectic manifolds is severely constrained, for example their odd Betti number
s are even. This remark leads to numerous examples of symplectic manifolds which are not Kähler, the first historical example is due to William Thurston
.
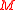 be a (
be a (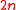 )-dimensional smooth manifold. Each element
)-dimensional smooth manifold. Each element
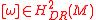
of the second de Rham cohomology
space of induces a map
induces a map
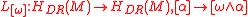
called the Lefschetz map of . Letting
. Letting 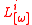 be the
be the  th iteration of
th iteration of 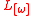 , we have for each
, we have for each 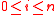 a map
a map
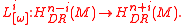
If is compact
is compact
and oriented, then Poincaré duality
tells us that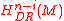 and
and 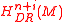 are vector spaces of the same dimension, so in these cases it is natural to ask whether or not the various iterations of Lefschetz maps are isomorphisms.
are vector spaces of the same dimension, so in these cases it is natural to ask whether or not the various iterations of Lefschetz maps are isomorphisms.
The Hard Lefschetz theorem states that this is the case for the symplectic form of a compact Kähler manifold.
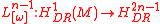
and
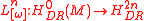
are isomorphisms, then is a Lefschetz element, or Lefschetz class. If
is a Lefschetz element, or Lefschetz class. If
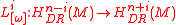
is an isomorphism for all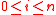 , then
, then  is a strong Lefschetz element, or a strong Lefschetz class.
is a strong Lefschetz element, or a strong Lefschetz class.
Let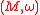 be a
be a 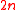 -dimensional symplectic manifold
-dimensional symplectic manifold
.Then it is orientable, but maybe not compact. One says that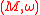 is a Lefschetz manifold if
is a Lefschetz manifold if  is a Lefschetz element, and
is a Lefschetz element, and 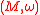 is a strong Lefschetz manifold if
is a strong Lefschetz manifold if  is a strong Lefschetz element.
is a strong Lefschetz element.
is a symplectic manifold. The strong Lefschetz theorem tells us that it is also a strong Lefschetz manifold, and hence a Lefschetz manifold. Therefore we have the following chain of inclusions.
{Kähler manifolds}  {strong Lefschetz manifolds}
{strong Lefschetz manifolds}  {Lefschetz manifolds}
{Lefschetz manifolds}  {symplectic manifolds}
{symplectic manifolds}
In , Chal Benson and Carolyn S. Gordon proved that if a compact nilmanifold
is a Lefschetz manifold, then it is diffeomorphic to a torus
. The fact that there are nilmanifolds that are not diffeomorphic to a torus shows that there is some space between Kähler manifolds and symplectic manifolds, but the class of nilmanifolds fails to show any differences between Kähler manifolds, Lefschetz manifolds, and strong Lefschetz manifolds.
Gordan and Benson conjectured that if a compact complete solvmanifold admits a Kähler structure, then it is diffeomorphic to a torus
. This has been proved. Furthermore, many examples have been found of solvmanifolds that are strong Lefschetz but not Kähler, and solvmanifolds that are Lefschetz but not strong Lefschetz. Such examples can be found in .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lefschetz manifold is a particular kind of symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
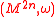 , sharing a certain cohomological property with Kaehler manifolds, that of satisfying the conclusion of the Hard Lefschetz theorem. More precisely, the strong Lefschetz property asks that for
, sharing a certain cohomological property with Kaehler manifolds, that of satisfying the conclusion of the Hard Lefschetz theorem. More precisely, the strong Lefschetz property asks that for 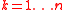 , the cup product
, the cup product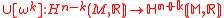
be an isomorphism.
The topology of these symplectic manifolds is severely constrained, for example their odd Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s are even. This remark leads to numerous examples of symplectic manifolds which are not Kähler, the first historical example is due to William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
.
Lefschetz maps
Let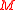 be a (
be a (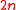 )-dimensional smooth manifold. Each element
)-dimensional smooth manifold. Each element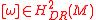
of the second de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
space of
 induces a map
induces a map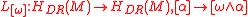
called the Lefschetz map of
 . Letting
. Letting 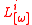 be the
be the  th iteration of
th iteration of 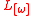 , we have for each
, we have for each 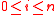 a map
a map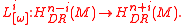
If
 is compact
is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and oriented, then Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
tells us that
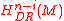 and
and 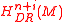 are vector spaces of the same dimension, so in these cases it is natural to ask whether or not the various iterations of Lefschetz maps are isomorphisms.
are vector spaces of the same dimension, so in these cases it is natural to ask whether or not the various iterations of Lefschetz maps are isomorphisms.The Hard Lefschetz theorem states that this is the case for the symplectic form of a compact Kähler manifold.
Definitions
If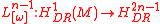
and
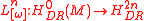
are isomorphisms, then
 is a Lefschetz element, or Lefschetz class. If
is a Lefschetz element, or Lefschetz class. If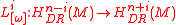
is an isomorphism for all
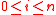 , then
, then  is a strong Lefschetz element, or a strong Lefschetz class.
is a strong Lefschetz element, or a strong Lefschetz class.Let
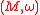 be a
be a 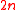 -dimensional symplectic manifold
-dimensional symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
.Then it is orientable, but maybe not compact. One says that
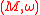 is a Lefschetz manifold if
is a Lefschetz manifold if  is a Lefschetz element, and
is a Lefschetz element, and 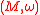 is a strong Lefschetz manifold if
is a strong Lefschetz manifold if  is a strong Lefschetz element.
is a strong Lefschetz element.Where to find Lefschetz manifolds
The real manifold underlying any Kähler manifoldKähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
is a symplectic manifold. The strong Lefschetz theorem tells us that it is also a strong Lefschetz manifold, and hence a Lefschetz manifold. Therefore we have the following chain of inclusions.
 {strong Lefschetz manifolds}
{strong Lefschetz manifolds}  {Lefschetz manifolds}
{Lefschetz manifolds}  {symplectic manifolds}
{symplectic manifolds}In , Chal Benson and Carolyn S. Gordon proved that if a compact nilmanifold
Nilmanifold
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space N/H, the quotient of a nilpotent Lie group N modulo a closed...
is a Lefschetz manifold, then it is diffeomorphic to a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. The fact that there are nilmanifolds that are not diffeomorphic to a torus shows that there is some space between Kähler manifolds and symplectic manifolds, but the class of nilmanifolds fails to show any differences between Kähler manifolds, Lefschetz manifolds, and strong Lefschetz manifolds.
Gordan and Benson conjectured that if a compact complete solvmanifold admits a Kähler structure, then it is diffeomorphic to a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. This has been proved. Furthermore, many examples have been found of solvmanifolds that are strong Lefschetz but not Kähler, and solvmanifolds that are Lefschetz but not strong Lefschetz. Such examples can be found in .

