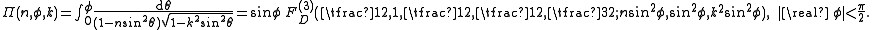Lauricella hypergeometric series
Encyclopedia
In 1893 Giuseppe Lauricella
defined and studied four hypergeometric series
FA, FB, FC, FD of three variables. They are :
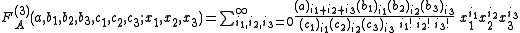
for |x1| + |x2| + |x3| < 1 and
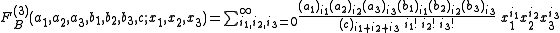
for |x1| < 1, |x2| < 1, |x3| < 1 and
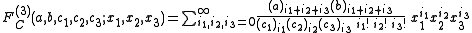
for |x1|½ + |x2|½ + |x3|½ < 1 and
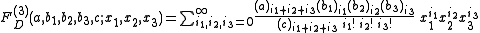
for |x1| < 1, |x2| < 1, |x3| < 1. Here the Pochhammer symbol
(q)i indicates the i-th rising factorial power of q, i.e.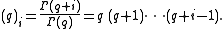
These functions can be extended to other values of the variables x1, x2, x3 by means of analytic continuation
.
Lauricella also indicated the existence of ten other hypergeometric functions of three variables. These were named FE, FF, ..., FT and studied by Shanti Saran in 1954 . There are therefore a total of 14 Lauricella–Saran hypergeometric functions.
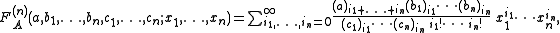
where |x1| + ... + |xn| < 1. These generalized series too are sometimes referred to as Lauricella functions.
When n = 2, the Lauricella functions correspond to the Appell hypergeometric series
of two variables as follows:
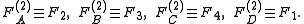
When n = 1, all four functions reduce to the Gauss hypergeometric function,
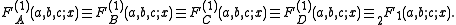
, Lauricella's FD can be written as a one-dimensional Euler
-type integral
for any number n of variables:
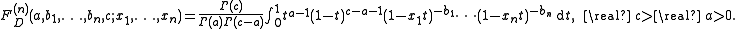
This representation can be easily verified by means of Taylor expansion
of the integrand, followed by termwise integration. The representation implies that the incomplete elliptic integral
Π is a special case of Lauricella's function FD with three variables:
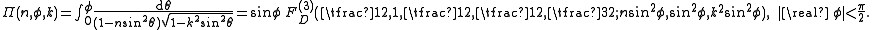
Giuseppe Lauricella
Giuseppe Lauricella was an Italian mathematician who is remembered today for his contributions to analysis and the theory of elasticity....
defined and studied four hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
FA, FB, FC, FD of three variables. They are :
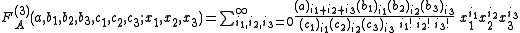
for |x1| + |x2| + |x3| < 1 and
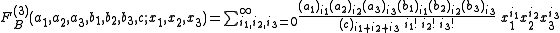
for |x1| < 1, |x2| < 1, |x3| < 1 and
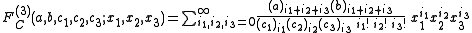
for |x1|½ + |x2|½ + |x3|½ < 1 and
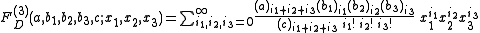
for |x1| < 1, |x2| < 1, |x3| < 1. Here the Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
(q)i indicates the i-th rising factorial power of q, i.e.
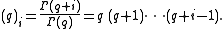
These functions can be extended to other values of the variables x1, x2, x3 by means of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
.
Lauricella also indicated the existence of ten other hypergeometric functions of three variables. These were named FE, FF, ..., FT and studied by Shanti Saran in 1954 . There are therefore a total of 14 Lauricella–Saran hypergeometric functions.
Generalization to n variables
These functions can be straightforwardly extended to n variables. One writes for example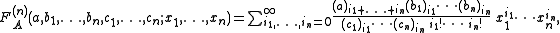
where |x1| + ... + |xn| < 1. These generalized series too are sometimes referred to as Lauricella functions.
When n = 2, the Lauricella functions correspond to the Appell hypergeometric series
Appell series
In mathematics, Appell series are a set of four hypergeometric series F1, F2, F3, F4 of two variables that were introduced by and that generalize Gauss's hypergeometric series 2F1 of one variable...
of two variables as follows:
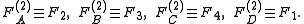
When n = 1, all four functions reduce to the Gauss hypergeometric function,
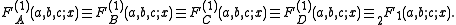
Integral representation of FD
In analogy with Appell's function F1Appell series
In mathematics, Appell series are a set of four hypergeometric series F1, F2, F3, F4 of two variables that were introduced by and that generalize Gauss's hypergeometric series 2F1 of one variable...
, Lauricella's FD can be written as a one-dimensional Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
-type integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
for any number n of variables:
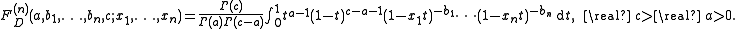
This representation can be easily verified by means of Taylor expansion
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of the integrand, followed by termwise integration. The representation implies that the incomplete elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
Π is a special case of Lauricella's function FD with three variables: