
Krull ring
Encyclopedia
In commutative algebra, a Krull ring or Krull domain is a commutative ring
with a well behaved theory of prime factorization. They were introduced by .
 be an integral domain and let
be an integral domain and let 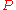 be the set of all prime ideal
be the set of all prime ideal
s of of height one, that is, the set of all prime ideals properly containing no nonzero prime ideal. Then
of height one, that is, the set of all prime ideals properly containing no nonzero prime ideal. Then  is a Krull ring if and only if
is a Krull ring if and only if
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with a well behaved theory of prime factorization. They were introduced by .
Formal definition
Let be an integral domain and let
be an integral domain and let 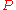 be the set of all prime ideal
be the set of all prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s of
 of height one, that is, the set of all prime ideals properly containing no nonzero prime ideal. Then
of height one, that is, the set of all prime ideals properly containing no nonzero prime ideal. Then  is a Krull ring if and only if
is a Krull ring if and only if
-
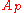 is a discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
is a discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
for all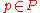 , and
, and - every non-zero principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
is the intersection of a finite number of primary idealPrimary idealIn mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
s of height one.
Properties
A Krull domain is a UFD if and only if every prime ideal of height one is principal.Examples
- Every integrally closed noetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
domain is a Krull ring. In particular, Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
s are Krull rings. Conversely Krull rings are integrally closed, so a Noetherian domain is Krull if and only if it is integrally closed. - If
 is a Krull ring then so is the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
is a Krull ring then so is the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
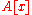 and the formal power series ring
and the formal power series ring 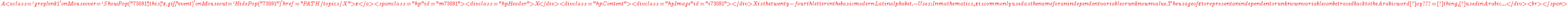 .
. - The polynomial ring
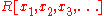 in infinitely many variables over a unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
in infinitely many variables over a unique factorization domainUnique factorization domainIn mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
 is a Krull ring which is not noetherian. In general, any unique factorization domain is a Krull ring.
is a Krull ring which is not noetherian. In general, any unique factorization domain is a Krull ring. - Let
 be a noetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
be a noetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
domain with quotient field , and
, and 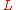 be a finite algebraic extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
be a finite algebraic extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of . Then the integral closure of
. Then the integral closure of  in
in 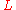 is a Krull ring.
is a Krull ring.

