Krener's theorem
Encyclopedia
In mathematics, Krener's theorem is a result in geometric control theory
about the topological properties of attainable sets of finite-dimensional control systems. It states that any attainable set of a bracket-generating system has nonempty interior or, equivalently, that any attainable set has nonempty interior in the topology of the corresponding orbit. Heuristically, Krener's theorem prohibits attainable sets from being hairy
.
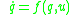
be a smooth control system, where
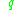
belongs to a finite-dimensional manifold
and 
belongs to a control set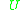 
. Consider the family of vector fields 
.
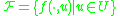Let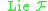
be the Lie algebra
generated by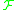
with respect to the Lie bracket of vector fields
.
Given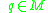
, if the vector space 
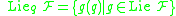is equal to 
,
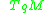then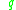
belongs to the closure of the interior of the attainable set from 
.
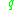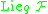is different from 
,
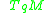the attainable set from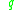
has nonempty interior in the orbit topology,
as it follows from Krener's theorem applied to the control system restricted to the orbit through
.
When all the vector fields in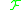
are analytic, 
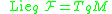if and only if 
belongs to the closure of the interior of the attainable set from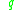 
. This is a consequence of Krener's theorem and of the orbit theorem.
As a corollary of Krener's theorem one can prove that if the system is bracket-generating and if the attainable set from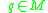
is dense in 
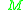, then the attainable set from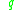 
is actually equal to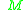
.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
about the topological properties of attainable sets of finite-dimensional control systems. It states that any attainable set of a bracket-generating system has nonempty interior or, equivalently, that any attainable set has nonempty interior in the topology of the corresponding orbit. Heuristically, Krener's theorem prohibits attainable sets from being hairy
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
.
Theorem
Let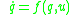be a smooth control system, where
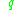
belongs to a finite-dimensional manifold
and belongs to a control set 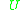. Consider the family of vector fields 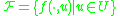.Let
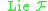be the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
generated by
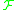with respect to the Lie bracket of vector fieldsLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
.
Given
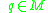, if the vector space 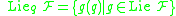is equal to 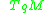,then
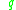belongs to the closure of the interior of the attainable set from 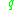.Remarks and consequences
Even if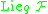 is different from 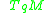,the attainable set from
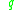has nonempty interior in the orbit topology,as it follows from Krener's theorem applied to the control system restricted to the orbit through
.When all the vector fields in
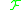are analytic, 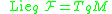if and only if belongs to the closure of the interior of the attainable set from 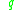. This is a consequence of Krener's theorem and of the orbit theorem.As a corollary of Krener's theorem one can prove that if the system is bracket-generating and if the attainable set from
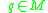is dense in 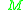, then the attainable set from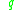 is actually equal to
.
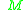