
Krein space
Encyclopedia
In mathematics
, in the field of functional analysis
, an indefinite inner product space
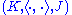
is an infinite-dimensional complex vector space
 equipped with both an indefinite
equipped with both an indefinite
inner product

and a positive semi-definite inner product
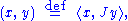
where the metric operator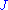 is an endomorphism
is an endomorphism
of obeying
obeying

The indefinite inner product space itself is not necessarily a Hilbert space
; but the existence of a positive semi-definite inner product on implies that one can form a quotient space
implies that one can form a quotient space
on which there is a positive definite inner product. Given a strong enough topology
on this quotient space, it has the structure of a Hilbert space, and many objects of interest in typical applications fall into this quotient space.
An indefinite inner product space is called a Krein space (or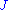 -space) if
-space) if 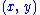 is positive definite and
is positive definite and  possesses a majorant topology. Krein spaces are named in honor of the Ukrainian
possesses a majorant topology. Krein spaces are named in honor of the Ukrainian
mathematician Mark Grigorievich Krein (3 April 1907 – 17 October 1989).
 equipped with an indefinite hermitian form
equipped with an indefinite hermitian form 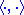 . In the theory of Krein spaces it is common to call such a hermitian form an indefinite inner product. The following subsets are defined in terms of the square norm induced by the indefinite inner product:
. In the theory of Krein spaces it is common to call such a hermitian form an indefinite inner product. The following subsets are defined in terms of the square norm induced by the indefinite inner product:
 ("neutral")
("neutral")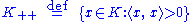 ("positive")
("positive") ("negative")
("negative")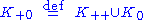 ("non-negative")
("non-negative")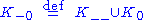 ("non-positive")
("non-positive")
A subspace
 lying within
lying within 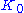 is called a neutral subspace. Similarly, a subspace lying within
is called a neutral subspace. Similarly, a subspace lying within  (
(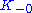 ) is called positive (negative) semi-definite, and a subspace lying within
) is called positive (negative) semi-definite, and a subspace lying within 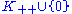 (
(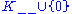 ) is called positive (negative) definite. A subspace in any of the above categories may be called semi-definite, and any subspace that is not semi-definite is called indefinite.
) is called positive (negative) definite. A subspace in any of the above categories may be called semi-definite, and any subspace that is not semi-definite is called indefinite.
Let our indefinite inner product space also be equipped with a decomposition into a pair of subspaces , called the fundamental decomposition, which respects the complex structure on
, called the fundamental decomposition, which respects the complex structure on  . Hence the corresponding linear projection operators
. Hence the corresponding linear projection operators
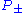 coincide with the identity on
coincide with the identity on  and annihilate
and annihilate 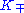 , and they commute with multiplication by the
, and they commute with multiplication by the 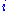 of the complex structure. If this decomposition is such that
of the complex structure. If this decomposition is such that 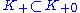 and
and 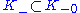 , then
, then  is called an indefinite inner product space; if
is called an indefinite inner product space; if 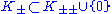 , then
, then  is called a Krein space, subject to the existence of a majorant topology on
is called a Krein space, subject to the existence of a majorant topology on  .
.
The operator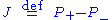 is called the (real phase) metric operator or fundamental symmetry, and may be used to define the Hilbert inner product
is called the (real phase) metric operator or fundamental symmetry, and may be used to define the Hilbert inner product 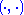 :
:
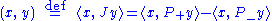
On a Krein space, the Hilbert inner product is positive definite, giving the structure of a Hilbert space (under a suitable topology). Under the weaker constraint
the structure of a Hilbert space (under a suitable topology). Under the weaker constraint 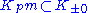 , some elements of the neutral subspace
, some elements of the neutral subspace 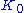 may still be neutral in the Hilbert inner product, but many are not. For instance, the subspaces
may still be neutral in the Hilbert inner product, but many are not. For instance, the subspaces 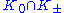 are part of the neutral subspace of the Hilbert inner product, because an element
are part of the neutral subspace of the Hilbert inner product, because an element 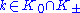 obeys
obeys  . But an element
. But an element 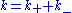 (
(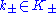 ) which happens to lie in
) which happens to lie in 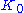 because
because 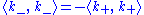 will have a positive square norm under the Hilbert inner product.
will have a positive square norm under the Hilbert inner product.
We note that the definition of the indefinite inner product as a Hermitian form implies that:
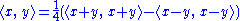
Therefore the indefinite inner product of any two elements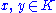 which differ only by an element
which differ only by an element 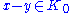 is equal to the square norm of their average
is equal to the square norm of their average  . Consequently, the inner product of any non-zero element
. Consequently, the inner product of any non-zero element 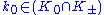 with any other element
with any other element 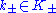 must be zero, lest we should be able to construct some
must be zero, lest we should be able to construct some  whose inner product with
whose inner product with 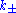 has the wrong sign to be the square norm of
has the wrong sign to be the square norm of 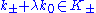 .
.
Similar arguments about the Hilbert inner product (which can be demonstrated to be a Hermitian form, therefore justifying the name "inner product") lead to the conclusion that its neutral space is precisely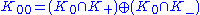 , that elements of this neutral space have zero Hilbert inner product with any element of
, that elements of this neutral space have zero Hilbert inner product with any element of  , and that the Hilbert inner product is positive semi-definite. It therefore induces a positive definite inner product (also denoted
, and that the Hilbert inner product is positive semi-definite. It therefore induces a positive definite inner product (also denoted 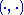 ) on the quotient space
) on the quotient space 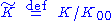 , which is the direct sum of
, which is the direct sum of 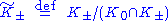 . Thus
. Thus 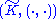 is a Hilbert space
is a Hilbert space
(given a suitable topology).
In many applications the positive semi-definite inner product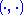 depends on the chosen fundamental decomposition, which is, in general, not unique. But it may be demonstrated (e. g., cf. Proposition 1.1 and 1.2 in the paper of H. Langer below) that any two metric operators
depends on the chosen fundamental decomposition, which is, in general, not unique. But it may be demonstrated (e. g., cf. Proposition 1.1 and 1.2 in the paper of H. Langer below) that any two metric operators 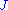 and
and 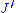 compatible with the same indefinite inner product on
compatible with the same indefinite inner product on  result in Hilbert spaces
result in Hilbert spaces  and
and  whose decompositions
whose decompositions 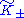 and
and 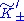 have equal dimensions. Although the Hilbert inner products on these quotient spaces do not generally coincide, they induce identical square norms, in the sense that the square norms of the equivalence classes
have equal dimensions. Although the Hilbert inner products on these quotient spaces do not generally coincide, they induce identical square norms, in the sense that the square norms of the equivalence classes 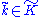 and
and 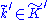 into which a given
into which a given 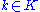 falls are equal. All topological notions in a Krein space, like continuity
falls are equal. All topological notions in a Krein space, like continuity
, closed
-ness of sets, and the spectrum
of an operator on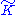 , are understood with respect to this Hilbert space topology
, are understood with respect to this Hilbert space topology
.
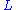 ,
, 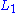 ,
, 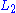 be subspaces of
be subspaces of  . The subspace
. The subspace
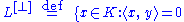 for all
for all 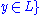 is called the orthogonal companion of
is called the orthogonal companion of 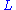 , and
, and 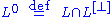 is the isotropic part of
is the isotropic part of 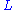 . If
. If  ,
, 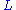 is called non-degenerate; otherwise it is degenerate. If
is called non-degenerate; otherwise it is degenerate. If 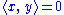 for all
for all 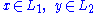 , then the two subspaces are said to be orthogonal, and we write
, then the two subspaces are said to be orthogonal, and we write 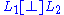 . If
. If 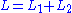 where
where 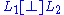 , we write
, we write  . If, in addition, this is a direct sum, we write
. If, in addition, this is a direct sum, we write 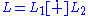 .
.
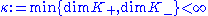 , the Krein space
, the Krein space 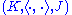 is called a Pontrjagin space or
is called a Pontrjagin space or  -space. (Conventionally, the indefinite inner product is given the sign that makes
-space. (Conventionally, the indefinite inner product is given the sign that makes 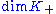 finite.) In this case
finite.) In this case 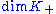 is known as the number of positive squares of
is known as the number of positive squares of 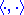 . Pontrjagin spaces are named after Lev Semenovich Pontryagin
. Pontrjagin spaces are named after Lev Semenovich Pontryagin
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, an indefinite inner product space
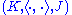
is an infinite-dimensional complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
 equipped with both an indefinite
equipped with both an indefiniteDefinite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
inner product

and a positive semi-definite inner product
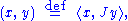
where the metric operator
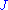 is an endomorphism
is an endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of
 obeying
obeying
The indefinite inner product space itself is not necessarily a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
; but the existence of a positive semi-definite inner product on
 implies that one can form a quotient space
implies that one can form a quotient spaceQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
on which there is a positive definite inner product. Given a strong enough topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on this quotient space, it has the structure of a Hilbert space, and many objects of interest in typical applications fall into this quotient space.
An indefinite inner product space is called a Krein space (or
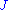 -space) if
-space) if 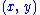 is positive definite and
is positive definite and  possesses a majorant topology. Krein spaces are named in honor of the Ukrainian
possesses a majorant topology. Krein spaces are named in honor of the UkrainianUkraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
mathematician Mark Grigorievich Krein (3 April 1907 – 17 October 1989).
Inner products and the metric operator
Consider a complex vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
 equipped with an indefinite hermitian form
equipped with an indefinite hermitian form 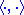 . In the theory of Krein spaces it is common to call such a hermitian form an indefinite inner product. The following subsets are defined in terms of the square norm induced by the indefinite inner product:
. In the theory of Krein spaces it is common to call such a hermitian form an indefinite inner product. The following subsets are defined in terms of the square norm induced by the indefinite inner product: ("neutral")
("neutral")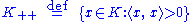 ("positive")
("positive") ("negative")
("negative")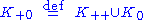 ("non-negative")
("non-negative")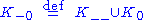 ("non-positive")
("non-positive")A subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
 lying within
lying within 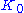 is called a neutral subspace. Similarly, a subspace lying within
is called a neutral subspace. Similarly, a subspace lying within  (
(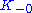 ) is called positive (negative) semi-definite, and a subspace lying within
) is called positive (negative) semi-definite, and a subspace lying within 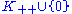 (
(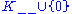 ) is called positive (negative) definite. A subspace in any of the above categories may be called semi-definite, and any subspace that is not semi-definite is called indefinite.
) is called positive (negative) definite. A subspace in any of the above categories may be called semi-definite, and any subspace that is not semi-definite is called indefinite.Let our indefinite inner product space also be equipped with a decomposition into a pair of subspaces
 , called the fundamental decomposition, which respects the complex structure on
, called the fundamental decomposition, which respects the complex structure on  . Hence the corresponding linear projection operators
. Hence the corresponding linear projection operatorsProjection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
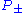 coincide with the identity on
coincide with the identity on  and annihilate
and annihilate 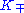 , and they commute with multiplication by the
, and they commute with multiplication by the 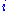 of the complex structure. If this decomposition is such that
of the complex structure. If this decomposition is such that 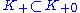 and
and 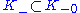 , then
, then  is called an indefinite inner product space; if
is called an indefinite inner product space; if 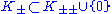 , then
, then  is called a Krein space, subject to the existence of a majorant topology on
is called a Krein space, subject to the existence of a majorant topology on  .
.The operator
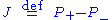 is called the (real phase) metric operator or fundamental symmetry, and may be used to define the Hilbert inner product
is called the (real phase) metric operator or fundamental symmetry, and may be used to define the Hilbert inner product 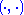 :
: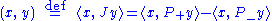
On a Krein space, the Hilbert inner product is positive definite, giving
 the structure of a Hilbert space (under a suitable topology). Under the weaker constraint
the structure of a Hilbert space (under a suitable topology). Under the weaker constraint 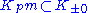 , some elements of the neutral subspace
, some elements of the neutral subspace 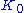 may still be neutral in the Hilbert inner product, but many are not. For instance, the subspaces
may still be neutral in the Hilbert inner product, but many are not. For instance, the subspaces 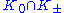 are part of the neutral subspace of the Hilbert inner product, because an element
are part of the neutral subspace of the Hilbert inner product, because an element 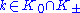 obeys
obeys  . But an element
. But an element 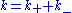 (
(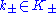 ) which happens to lie in
) which happens to lie in 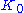 because
because 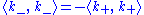 will have a positive square norm under the Hilbert inner product.
will have a positive square norm under the Hilbert inner product.We note that the definition of the indefinite inner product as a Hermitian form implies that:
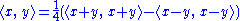
Therefore the indefinite inner product of any two elements
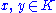 which differ only by an element
which differ only by an element 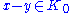 is equal to the square norm of their average
is equal to the square norm of their average  . Consequently, the inner product of any non-zero element
. Consequently, the inner product of any non-zero element 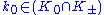 with any other element
with any other element 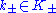 must be zero, lest we should be able to construct some
must be zero, lest we should be able to construct some  whose inner product with
whose inner product with 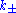 has the wrong sign to be the square norm of
has the wrong sign to be the square norm of 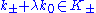 .
.Similar arguments about the Hilbert inner product (which can be demonstrated to be a Hermitian form, therefore justifying the name "inner product") lead to the conclusion that its neutral space is precisely
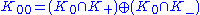 , that elements of this neutral space have zero Hilbert inner product with any element of
, that elements of this neutral space have zero Hilbert inner product with any element of  , and that the Hilbert inner product is positive semi-definite. It therefore induces a positive definite inner product (also denoted
, and that the Hilbert inner product is positive semi-definite. It therefore induces a positive definite inner product (also denoted 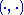 ) on the quotient space
) on the quotient space 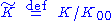 , which is the direct sum of
, which is the direct sum of 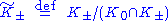 . Thus
. Thus 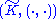 is a Hilbert space
is a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
(given a suitable topology).
Properties and applications
Krein spaces arise naturally in situations where the indefinite inner product has an analytically useful property (such as Lorentz invariance) which the Hilbert inner product lacks. It is also common for one of the two inner products, usually the indefinite one, to be globally defined on a manifold and the other to be coordinate-dependent and therefore defined only on a local section.In many applications the positive semi-definite inner product
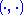 depends on the chosen fundamental decomposition, which is, in general, not unique. But it may be demonstrated (e. g., cf. Proposition 1.1 and 1.2 in the paper of H. Langer below) that any two metric operators
depends on the chosen fundamental decomposition, which is, in general, not unique. But it may be demonstrated (e. g., cf. Proposition 1.1 and 1.2 in the paper of H. Langer below) that any two metric operators 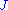 and
and 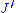 compatible with the same indefinite inner product on
compatible with the same indefinite inner product on  result in Hilbert spaces
result in Hilbert spaces  and
and  whose decompositions
whose decompositions 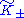 and
and 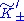 have equal dimensions. Although the Hilbert inner products on these quotient spaces do not generally coincide, they induce identical square norms, in the sense that the square norms of the equivalence classes
have equal dimensions. Although the Hilbert inner products on these quotient spaces do not generally coincide, they induce identical square norms, in the sense that the square norms of the equivalence classes 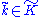 and
and 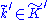 into which a given
into which a given 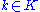 falls are equal. All topological notions in a Krein space, like continuity
falls are equal. All topological notions in a Krein space, like continuityContinuity
Continuity may refer to:In mathematics:* The opposing concept to discreteness; common examples include:** Continuous probability distribution or random variable in probability and statistics...
, closed
Closed
Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
-ness of sets, and the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of an operator on
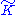 , are understood with respect to this Hilbert space topology
, are understood with respect to this Hilbert space topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Isotropic part and degenerate subspaces
Let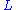 ,
, 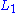 ,
, 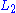 be subspaces of
be subspaces of  . The subspace
. The subspaceSubspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
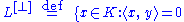 for all
for all 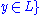 is called the orthogonal companion of
is called the orthogonal companion of 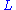 , and
, and 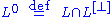 is the isotropic part of
is the isotropic part of 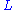 . If
. If  ,
, 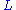 is called non-degenerate; otherwise it is degenerate. If
is called non-degenerate; otherwise it is degenerate. If 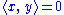 for all
for all 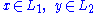 , then the two subspaces are said to be orthogonal, and we write
, then the two subspaces are said to be orthogonal, and we write 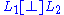 . If
. If 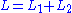 where
where 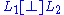 , we write
, we write  . If, in addition, this is a direct sum, we write
. If, in addition, this is a direct sum, we write 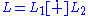 .
.Pontrjagin space
If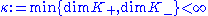 , the Krein space
, the Krein space 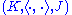 is called a Pontrjagin space or
is called a Pontrjagin space or  -space. (Conventionally, the indefinite inner product is given the sign that makes
-space. (Conventionally, the indefinite inner product is given the sign that makes 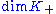 finite.) In this case
finite.) In this case 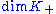 is known as the number of positive squares of
is known as the number of positive squares of 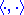 . Pontrjagin spaces are named after Lev Semenovich Pontryagin
. Pontrjagin spaces are named after Lev Semenovich PontryaginLev Semenovich Pontryagin
Lev Semenovich Pontryagin was a Soviet mathematician. He was born in Moscow and lost his eyesight due to a primus stove explosion when he was 14...
.

