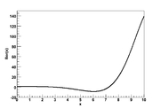
Kelvin functions
Encyclopedia
In applied mathematics, the Kelvin functions Berν(x) and Beiν(x) are the real and imaginary parts, respectively, of
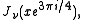
where x is real, and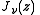
is the νth order Bessel function
of the first kind. Similarly, the functions Kerν(x) and Keiν(x) are the real and imaginary parts, respectively, of
,
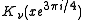where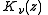
is the νth order modified Bessel function of the second kind.
These functions are named after William Thomson, 1st Baron Kelvin
.
While the Kelvin functions are defined as the real and imaginary parts of Bessel functions with x taken to be real, the functions can be analytically continued for complex arguments x ei φ, φ ∈ [0, 2π). With the exception of Bern(x) and Bein(x) for integral n, the Kelvin functions have a branch point
at x = 0.
For integers n, Bern(x) has the series expansion
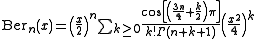
where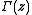
is the Gamma function
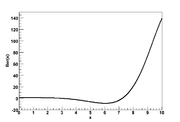
. The special case Ber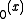
, commonly denoted as just Ber(x), has the series expansion
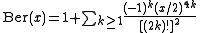
and asymptotic series
,
where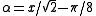
, and
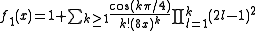
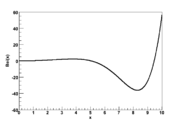
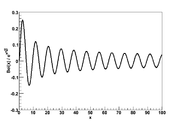For integers 
, Bei
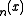has the series expansion
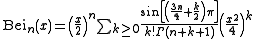
where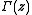
is the Gamma function
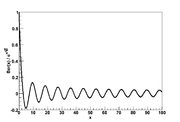
. The special case Bei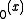
, commonly denoted as just Bei
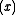, has the series expansion
and asymptotic series
,
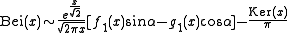where
, 
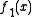, and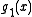 
are defined as for Ber
.
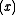where 
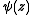is the Digamma function. The special case Ker
, commonly denoted as just Ker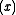
, has the series expansion
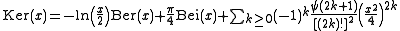
and the asymptotic series
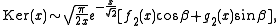
where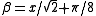
, and
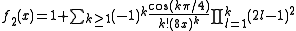
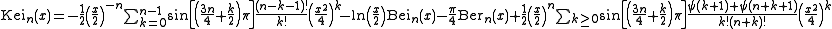
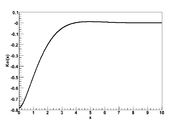
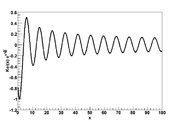where 
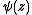is the Digamma function. The special case Kei
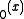, commonly denoted as just Kei
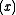, has the series expansion
and the asymptotic series
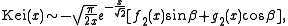
where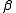
, 
, and 
are defined as for Ker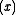
.
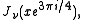
where x is real, and
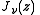
is the νth order Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind. Similarly, the functions Kerν(x) and Keiν(x) are the real and imaginary parts, respectively, of
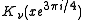, where
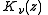is the νth order modified Bessel function of the second kind.These functions are named after William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
.
While the Kelvin functions are defined as the real and imaginary parts of Bessel functions with x taken to be real, the functions can be analytically continued for complex arguments x ei φ, φ ∈ [0, 2π). With the exception of Bern(x) and Bein(x) for integral n, the Kelvin functions have a branch point
Branch point
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...
at x = 0.
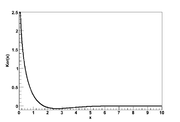
Ber(x)
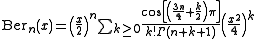
where
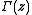is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. The special case Ber
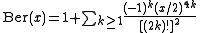
, commonly denoted as just Ber(x), has the series expansionand asymptotic series
,where
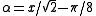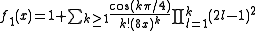
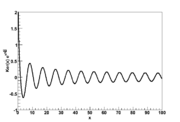
, andBei(x)
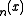, Bei has the series expansion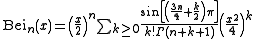where
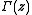is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. The special case Bei
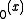, commonly denoted as just Bei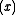, has the series expansionand asymptotic series
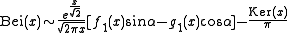,where
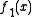, , and 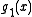are defined as for Ber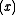.Ker(x)
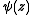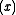For integers n, Kern(x) has the (complicated) series expansion is the Digamma function. The special case Ker, commonly denoted as just Ker, has the series expansion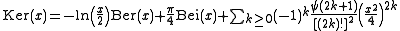and the asymptotic series
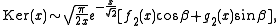
where
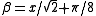, and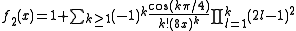Kei(x)
For integers n, Kein(x) has the (complicated) series expansion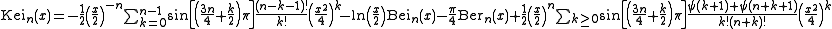 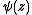is the Digamma function. The special case Kei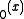, commonly denoted as just Kei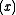, has the series expansionand the asymptotic series
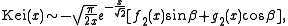
where
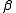, , and are defined as for Ker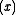.External links
- Weisstein, Eric W. "Kelvin Functions." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/KelvinFunctions.html
- GPL-licensed C/C++ source code for calculating Kelvin functions at codecogs.com: http://www.codecogs.com/d-ox/maths/special/bessel/kelvin.php