K-nearest neighbor algorithm
Overview
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
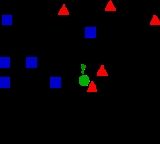
, the k-nearest neighbor algorithm (k-NN) is a method for classifying objects based on closest training examples in the feature space
Feature space
In pattern recognition a feature space is an abstract space where each pattern sample is represented as a point in n-dimensional space. Its dimension is determined by the number of features used to describe the patterns...
. k-NN is a type of instance-based learning
Instance-based learning
In machine learning, instance-based learning or memory-based learning is a family of learning algorithms that, instead of performing explicit generalization, compare new problem instances with instances seen in training, which have been stored in memory...
, or lazy learning
Lazy learning
In artificial intelligence, lazy learning is a learning method in which generalization beyond the training data is delayed until a query is made to the system, as opposed to in eager learning, where the system tries to generalize the training data before receiving queries.The main advantage gained...
where the function is only approximated locally and all computation is deferred until classification. The k-nearest neighbor algorithm is amongst the simplest of all machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
algorithms: an object is classified by a majority vote of its neighbors, with the object being assigned to the class most common amongst its k nearest neighbors (k is a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, typically small).
Discussions

