
Interval exchange transformation
Encyclopedia
In mathematics
, an interval exchange transformation is a kind of dynamical system
that generalises the idea of a circle rotation. The phase space consists of the unit interval
, and the transformation acts by cutting the interval into several subintervals, and then permuting these subintervals.
 and let
and let  be a permutation
be a permutation
on . Consider a vector
. Consider a vector
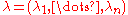
of positive real numbers (the widths of the subintervals), satisfying
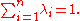
Define a map
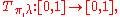
called the interval exchange transformation associated to the pair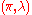 as follows. For
as follows. For
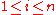
let
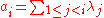 and let
and let
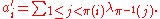
Then for , define
, define

if lies in the subinterval
lies in the subinterval 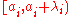 . Thus
. Thus  acts on each subinterval of the form
acts on each subinterval of the form  by an orientation-preserving isometry
by an orientation-preserving isometry
, and it rearranges these subintervals so that the subinterval at position is moved to position
is moved to position  .
.
 is a bijection
is a bijection
of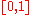 to itself which preserves Lebesgue measure
to itself which preserves Lebesgue measure
and is locally a translation. It is continuous except at a finite number of points.
The inverse
of the interval exchange transformation is again an interval exchange transformation. In fact, it is the transformation
is again an interval exchange transformation. In fact, it is the transformation 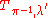 where
where 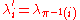 for all
for all 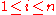 .
.
If and
and 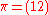 (in cycle notation
(in cycle notation
), and if we join up the ends of the interval to make a circle, then is just a circle rotation. The Weyl equidistribution theorem then asserts that if the length
is just a circle rotation. The Weyl equidistribution theorem then asserts that if the length 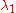 is irrational, then
is irrational, then  is uniquely ergodic. Roughly speaking, this means that the orbits of points of
is uniquely ergodic. Roughly speaking, this means that the orbits of points of 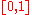 are uniformly evenly distributed. On the other hand, if
are uniformly evenly distributed. On the other hand, if 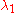 is rational then each point of the interval is periodic
is rational then each point of the interval is periodic
, and the period is the denominator of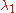 (written in lowest terms).
(written in lowest terms).
If , and provided
, and provided  satisfies certain non-degeneracy conditions, a deep theorem due independently to W.Veech and to H.Masur asserts that for almost all
satisfies certain non-degeneracy conditions, a deep theorem due independently to W.Veech and to H.Masur asserts that for almost all
choices of in the unit simplex
in the unit simplex 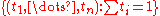 the interval exchange transformation
the interval exchange transformation  is again uniquely ergodic. However, for
is again uniquely ergodic. However, for  there also exist choices of
there also exist choices of 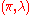 so that
so that  is ergodic but not uniquely ergodic. Even in these cases, the number of ergodic invariant
is ergodic but not uniquely ergodic. Even in these cases, the number of ergodic invariant
measures of is finite, and is at most
is finite, and is at most  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an interval exchange transformation is a kind of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
that generalises the idea of a circle rotation. The phase space consists of the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, and the transformation acts by cutting the interval into several subintervals, and then permuting these subintervals.
Formal definition
Let and let
and let  be a permutation
be a permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
on
 . Consider a vector
. Consider a vector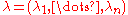
of positive real numbers (the widths of the subintervals), satisfying
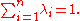
Define a map
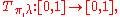
called the interval exchange transformation associated to the pair
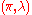 as follows. For
as follows. For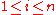
let
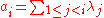 and let
and let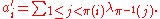
Then for
 , define
, define
if
 lies in the subinterval
lies in the subinterval 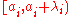 . Thus
. Thus  acts on each subinterval of the form
acts on each subinterval of the form  by an orientation-preserving isometry
by an orientation-preserving isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, and it rearranges these subintervals so that the subinterval at position
 is moved to position
is moved to position  .
.Properties
Any interval exchange transformation is a bijection
is a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
of
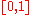 to itself which preserves Lebesgue measure
to itself which preserves Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
and is locally a translation. It is continuous except at a finite number of points.
The inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the interval exchange transformation
 is again an interval exchange transformation. In fact, it is the transformation
is again an interval exchange transformation. In fact, it is the transformation 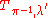 where
where 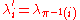 for all
for all 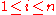 .
.If
 and
and 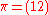 (in cycle notation
(in cycle notationCycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
), and if we join up the ends of the interval to make a circle, then
 is just a circle rotation. The Weyl equidistribution theorem then asserts that if the length
is just a circle rotation. The Weyl equidistribution theorem then asserts that if the length 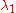 is irrational, then
is irrational, then  is uniquely ergodic. Roughly speaking, this means that the orbits of points of
is uniquely ergodic. Roughly speaking, this means that the orbits of points of 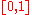 are uniformly evenly distributed. On the other hand, if
are uniformly evenly distributed. On the other hand, if 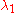 is rational then each point of the interval is periodic
is rational then each point of the interval is periodicFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, and the period is the denominator of
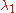 (written in lowest terms).
(written in lowest terms).If
 , and provided
, and provided  satisfies certain non-degeneracy conditions, a deep theorem due independently to W.Veech and to H.Masur asserts that for almost all
satisfies certain non-degeneracy conditions, a deep theorem due independently to W.Veech and to H.Masur asserts that for almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
choices of
 in the unit simplex
in the unit simplex 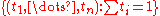 the interval exchange transformation
the interval exchange transformation  is again uniquely ergodic. However, for
is again uniquely ergodic. However, for  there also exist choices of
there also exist choices of 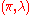 so that
so that  is ergodic but not uniquely ergodic. Even in these cases, the number of ergodic invariant
is ergodic but not uniquely ergodic. Even in these cases, the number of ergodic invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
measures of
 is finite, and is at most
is finite, and is at most  .
.
