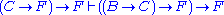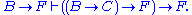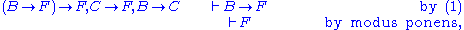Implicational propositional calculus
Encyclopedia
In mathematical logic
, the implicational propositional calculus is a version of classical
propositional calculus
which uses only one connective
, called implication or conditional
. In formula
s, this binary operation
is indicated by "implies", "if ..., then ...", "→", " ", etc..
", etc..
which is known to be false
and uses that as if it were a nullary connective for falsity, then one can define all other truth functions. So implication is virtually complete as an operator. If P,Q, and F are propositions and F is known to be false, then:
More generally, since the above operators are known to be functionally complete, it follows that any truth function can be expressed in terms of "→" and "F", if we have a proposition F which is known to be false.
It is worth noting that F is not definable from → and arbitrary sentence variables: any formula constructed from → and propositional variables must receive the value true when all of its variables are evaluated to true.
It follows as a corollary that {→} is not functionally complete. It cannot, for example, be used to define the two-place truth function that always returns false.
Where in each case
, P, Q, and R may be replaced by any formulas which contain only "→" as a connective. If Γ is a set of formulas and A a formula, then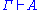 means that A is derivable using the axioms and rules above and formulas from Γ as additional hypotheses.
means that A is derivable using the axioms and rules above and formulas from Γ as additional hypotheses.
:
where σ is any substitution (of formulas using only implication).
The implicational propositional calculus also satisfies the deduction theorem
:
As explained in the deduction theorem
article, this holds for any axiomatic extension of the system consisting of axioms 1 and 2 above and modus ponens.
by Γ, then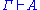 .
.
and the deduction theorem, we may reduce the completeness theorem to its special case with empty Γ, i.e., we only need to show that every tautology is derivable in the system.
The proof is similar to completeness of full propositional logic, but it also uses the following idea to overcome the functional incompleteness of implication. If A and F are formulas, then is equivalent to where A* is the result of replacing in A all, some, or none of the occurrences of F by falsity. Similarly, is equivalent to So under some conditions, one can use them as substitutes for saying A* is false or A* is true respectively.
We first observe some basic facts about derivability:
Let F be an arbitrary fixed formula. For any formula A, we define and Let us consider only formulas in propositional variables p1, ..., pn. We claim that for every formula A in these variables and every truth assignment
e,
We prove (4) by induction on A. The base case A = pi is trivial. Let We distinguish three cases:
Now let A be a tautology in variables p1, ..., pn. We will prove by reverse induction on k = n,...,0 that for every assignment e,
The base case k = n is a special case of (4). Assume that (5) holds for k + 1, we will show it for k. By applying deduction theorem to the induction hypothesis, we obtain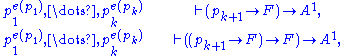
by first setting e(pk+1) = 0 and second setting e(pk+1) = 1. From this we derive (5) using (3).
For k = 0 we obtain that the formula A1, i.e., is provable without assumptions. Recall that F was an arbitrary formula, thus we can choose F = A, which gives us provability of the formula Since is provable by the deduction theorem, we can infer A.
This proof is constructive. That is, given a tautology, one could actually follow the instructions and create a proof of it from the axioms. However, the length of such a proof increases exponentially with the number of propositional variables in the tautology, hence it is not a practical method for any but the very shortest tautologies.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the implicational propositional calculus is a version of classical
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
propositional calculus
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
which uses only one connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
, called implication or conditional
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
. In formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s, this binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
is indicated by "implies", "if ..., then ...", "→", "
 ", etc..
", etc..Virtual completeness as an operator
Implication alone is not functionally complete as a logical operator because one cannot form all other two-valued truth functions from it. However, if one has a propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
which is known to be false
False
False or falsehood may refer to:*False *Lie or falsehood, a type of deception in the form of an untruthful statement*Falsity or falsehood, in law, deceitfulness by one party that results in damage to another...
and uses that as if it were a nullary connective for falsity, then one can define all other truth functions. So implication is virtually complete as an operator. If P,Q, and F are propositions and F is known to be false, then:
- ¬P is equivalentLogical equivalenceIn logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to P → F - P ∧ Q is equivalent to (P → (Q → F)) → F
- P ∨ Q is equivalent to (P → Q) → Q
- P ↔ Q is equivalent to ((P → Q) → ((Q → P) → F)) → F
More generally, since the above operators are known to be functionally complete, it follows that any truth function can be expressed in terms of "→" and "F", if we have a proposition F which is known to be false.
It is worth noting that F is not definable from → and arbitrary sentence variables: any formula constructed from → and propositional variables must receive the value true when all of its variables are evaluated to true.
It follows as a corollary that {→} is not functionally complete. It cannot, for example, be used to define the two-place truth function that always returns false.
Axiom system
- Axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
1 is P → (Q → P). - Axiom schema 2 is (P → (Q → R)) → ((P → Q) → (P → R)).
- Axiom schema 3 (Peirce's lawPeirce's lawIn logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...
) is ((P → Q) → P) → P. - The one non-nullary rule of inferenceRule of inferenceIn logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
(modus ponensModus ponensIn classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
) is: from P and P → Q infer Q.
Where in each case
Case analysis
Case analysis is one of the most general and applicable methods of analytical thinking, depending only on the division of a problem, decision or situation into a sufficient number of separate cases. Analysing each such case individually may be enough to resolve the initial question...
, P, Q, and R may be replaced by any formulas which contain only "→" as a connective. If Γ is a set of formulas and A a formula, then
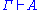 means that A is derivable using the axioms and rules above and formulas from Γ as additional hypotheses.
means that A is derivable using the axioms and rules above and formulas from Γ as additional hypotheses.Basis properties
Since all axioms and rules of the calculus are schemata, derivation is closed under substitutionSubstitution (logic)
Substitution is a fundamental concept in logic. Substitution is a syntactic transformation on strings of symbols of a formal language.In propositional logic, a substitution instance of a propositional formula is a second formula obtained by replacing symbols of the original formula by other formulas...
:
- If
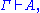 then
then 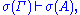
where σ is any substitution (of formulas using only implication).
The implicational propositional calculus also satisfies the deduction theorem
Deduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
:
- If
 , then
, then 
As explained in the deduction theorem
Deduction theorem
In mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
article, this holds for any axiomatic extension of the system consisting of axioms 1 and 2 above and modus ponens.
Completeness
The implicational propositional calculus is semantically complete with respect to the usual two-valued semantics of classical propositional logic. That is, if Γ is a set of implicational formulas, and A is an implicational formula entailedEntailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
by Γ, then
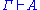 .
.Proof
A proof of the completeness theorem is outlined below. First, using the compactness theoremCompactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
and the deduction theorem, we may reduce the completeness theorem to its special case with empty Γ, i.e., we only need to show that every tautology is derivable in the system.
The proof is similar to completeness of full propositional logic, but it also uses the following idea to overcome the functional incompleteness of implication. If A and F are formulas, then is equivalent to where A* is the result of replacing in A all, some, or none of the occurrences of F by falsity. Similarly, is equivalent to So under some conditions, one can use them as substitutes for saying A* is false or A* is true respectively.
We first observe some basic facts about derivability:
-
- Indeed, we can derive A → (B → C) using Axiom 1, and then derive A → C by modus ponens (twice) from Ax. 2.
-
- This follows from (1) by the deduction theorem.
-
- If we further assume C → B, we can derive using (1), then we derive C by modus ponens. This shows
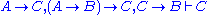 , and the deduction theorem gives
, and the deduction theorem gives 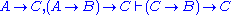 . We apply Ax. 3 to obtain (3).
. We apply Ax. 3 to obtain (3).
- If we further assume C → B, we can derive using (1), then we derive C by modus ponens. This shows
Let F be an arbitrary fixed formula. For any formula A, we define and Let us consider only formulas in propositional variables p1, ..., pn. We claim that for every formula A in these variables and every truth assignment
Valuation (logic)
In logic and model theory, a valuation can be:*In propositional logic, an assignment of truth values to propositional variables, with a corresponding assignment of truth values to all propositional formulas with those variables....
e,
We prove (4) by induction on A. The base case A = pi is trivial. Let We distinguish three cases:
- e(C) = 1. Then also e(A) = 1. We have
-
- by applying (2) twice to the axiom Since we have derived by the induction hypothesis, we can infer
-
- e(B) = 0. Then again e(A) = 1. The deduction theorem applied to (3) gives
-
- Since we have derived by the induction hypothesis, we can infer
-
- e(B) = 1 and e(C) = 0. Then e(A) = 0. We have
-
- thus
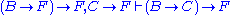 by the deduction theorem. We have derived and by the induction hypothesis, hence we can infer This completes the proof of (4).
by the deduction theorem. We have derived and by the induction hypothesis, hence we can infer This completes the proof of (4).
-
Now let A be a tautology in variables p1, ..., pn. We will prove by reverse induction on k = n,...,0 that for every assignment e,
The base case k = n is a special case of (4). Assume that (5) holds for k + 1, we will show it for k. By applying deduction theorem to the induction hypothesis, we obtain
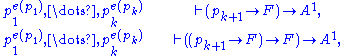
by first setting e(pk+1) = 0 and second setting e(pk+1) = 1. From this we derive (5) using (3).
For k = 0 we obtain that the formula A1, i.e., is provable without assumptions. Recall that F was an arbitrary formula, thus we can choose F = A, which gives us provability of the formula Since is provable by the deduction theorem, we can infer A.
This proof is constructive. That is, given a tautology, one could actually follow the instructions and create a proof of it from the axioms. However, the length of such a proof increases exponentially with the number of propositional variables in the tautology, hence it is not a practical method for any but the very shortest tautologies.
See also
- Propositional calculusPropositional calculusIn mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
- Deduction theoremDeduction theoremIn mathematical logic, the deduction theorem is a metatheorem of first-order logic. It is a formalization of the common proof technique in which an implication A → B is proved by assuming A and then proving B from this assumption. The deduction theorem explains why proofs of conditional...
- List of logic systems#Implicational propositional calculus
- Peirce's lawPeirce's lawIn logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...
- Tautology (logic)Tautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
- Truth tableTruth tableA truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
- Valuation (logic)Valuation (logic)In logic and model theory, a valuation can be:*In propositional logic, an assignment of truth values to propositional variables, with a corresponding assignment of truth values to all propositional formulas with those variables....