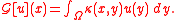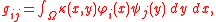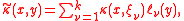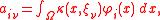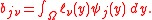Hierarchical matrix
Encyclopedia
In numerical mathematics, hierarchical matrices (H-matrices)
are used as data-sparse approximations of non-sparse matrices.
While a sparse matrix
of dimension can be represented efficiently in
can be represented efficiently in 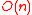 units of storage
units of storage
by storing only its non-zero entries, a non-sparse matrix would require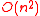 units of storage, and using this type
units of storage, and using this type
of matrices for large problems would therefore be prohibitively expensive in terms of storage and computing time.
Hierarchical matrices provide an approximation requiring only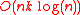 units of storage, where
units of storage, where  is a
is a
parameter controlling the accuracy of the approximation.
In typical applications, e.g., when discretizing integral equations
or solving elliptic partial differential equations
,
a rank proportional to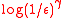 with a small constant
with a small constant  is sufficient to ensure an
is sufficient to ensure an
accuracy of .
.
Compared to many other data-sparse representations of non-sparse matrices, hierarchical matrices offer a major advantage:
the results of matrix arithmetic operations like matrix multiplication, factorization or inversion can be approximated
in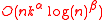 operations, where
operations, where 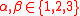
.
let be index sets, and let
be index sets, and let 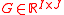 denote the matrix we have to approximate.
denote the matrix we have to approximate.
In many applications (see above), we can find subsets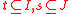 such that
such that 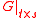
can be approximated by a rank- matrix.
matrix.
This approximation can be represented in factorized form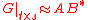 with factors
with factors
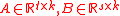 .
.
While the standard representation of the matrix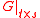 requires
requires  units of storage,
units of storage,
the factorized representation requires only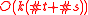 units.
units.
If is not too large, the storage requirements are reduced significantly.
is not too large, the storage requirements are reduced significantly.
In order to approximate the entire matrix , it is split into a family of submatrices.
, it is split into a family of submatrices.
Large submatrices are stored in factorized representation, while small submatrices are stored in standard representation
in order to improve the efficiency.
Low-rank matrices are closely related to degenerate expansions used in panel clustering and the fast multipole method
to approximate integral operators.
In this sense, hierarchical matrices can be considered the algebraic counterparts of these techniques.
appearing in the boundary element method
.
A typical operator has the form
The Galerkin method
leads to matrix entries of the form
where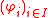 and
and 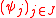 are families of finite element basis functions.
are families of finite element basis functions.
If the kernel function is sufficiently smooth, we can approximate it by polynomial interpolation
is sufficiently smooth, we can approximate it by polynomial interpolation
to obtain
where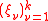 is the family of interpolation points and
is the family of interpolation points and 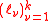
is the corresponding family of lagrange polynomial
s.
Replacing by
by  yields an approximation
yields an approximation
are used as data-sparse approximations of non-sparse matrices.
While a sparse matrix
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
of dimension
 can be represented efficiently in
can be represented efficiently in 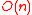 units of storage
units of storageby storing only its non-zero entries, a non-sparse matrix would require
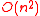 units of storage, and using this type
units of storage, and using this typeof matrices for large problems would therefore be prohibitively expensive in terms of storage and computing time.
Hierarchical matrices provide an approximation requiring only
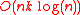 units of storage, where
units of storage, where  is a
is aparameter controlling the accuracy of the approximation.
In typical applications, e.g., when discretizing integral equations
or solving elliptic partial differential equations
,
a rank proportional to
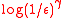 with a small constant
with a small constant  is sufficient to ensure an
is sufficient to ensure anaccuracy of
 .
.Compared to many other data-sparse representations of non-sparse matrices, hierarchical matrices offer a major advantage:
the results of matrix arithmetic operations like matrix multiplication, factorization or inversion can be approximated
in
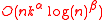 operations, where
operations, where 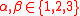
.
Basic idea
Hierarchical matrices rely on local low-rank approximations:let
 be index sets, and let
be index sets, and let 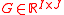 denote the matrix we have to approximate.
denote the matrix we have to approximate.In many applications (see above), we can find subsets
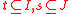 such that
such that 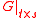
can be approximated by a rank-
 matrix.
matrix.This approximation can be represented in factorized form
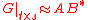 with factors
with factors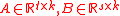 .
.While the standard representation of the matrix
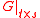 requires
requires  units of storage,
units of storage,the factorized representation requires only
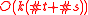 units.
units.If
 is not too large, the storage requirements are reduced significantly.
is not too large, the storage requirements are reduced significantly.In order to approximate the entire matrix
 , it is split into a family of submatrices.
, it is split into a family of submatrices.Large submatrices are stored in factorized representation, while small submatrices are stored in standard representation
in order to improve the efficiency.
Low-rank matrices are closely related to degenerate expansions used in panel clustering and the fast multipole method
Fast Multipole Method
The fast multipole method is a mathematical technique that was developed to speed up the calculation of long-ranged forces in the n-body problem...
to approximate integral operators.
In this sense, hierarchical matrices can be considered the algebraic counterparts of these techniques.
Application to integral operators
Hierarchical matrices are successfully used to treat integral equations, e.g., the single and double layer potential operatorsappearing in the boundary element method
Boundary element method
The boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
.
A typical operator has the form
The Galerkin method
Galerkin method
In mathematics, in the area of numerical analysis, Galerkin methods are a class of methods for converting a continuous operator problem to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a...
leads to matrix entries of the form
where
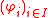 and
and 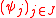 are families of finite element basis functions.
are families of finite element basis functions.If the kernel function
 is sufficiently smooth, we can approximate it by polynomial interpolation
is sufficiently smooth, we can approximate it by polynomial interpolationPolynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
to obtain
where
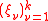 is the family of interpolation points and
is the family of interpolation points and 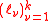
is the corresponding family of lagrange polynomial
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
s.
Replacing
 by
by  yields an approximation
yields an approximation-
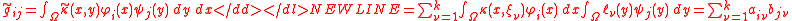
with the coefficients
If we choose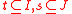 and use the same interpolation points for all
and use the same interpolation points for all  , we obtain
, we obtain
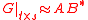 .
.
Obviously, any other approximation separating the variables and
and 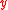 , e.g., the multipole expansion,
, e.g., the multipole expansion,
would also allow us to split the double integral into two single integrals and thus arrive at a similar factorized low-rank matrix.
Of particular interest are cross approximation techniques
that use only the entries of the original matrix to construct a low-rank approximation.
to construct a low-rank approximation.
Application to elliptic partial differential equations
Since the solution operator of an elliptic partial differential equation can be expressed as an integral operator involving
Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
, it is not surprising that the inverse of the stiffness matrix arising from the finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
can be approximated by a hierarchical matrix.
Green's function depends on the shape of the computational domain, therefore it is usually not known.
Nevertheless, approximate arithmetic operations can be employed to compute an approximate inverse without knowing the
function explicitly.
Surprisingly, it is possible to prove that the inverse can be approximated even if
the differential operator involves non-smooth coefficients and Green's function is therefore not smooth.
Arithmetic operations
The most important innovation of the hierarchical matrix method is the development of efficient algorithms for performing
(approximate) matrix arithmetic operations on non-sparse matrices, e.g., to compute approximate inverses, LU decompositionLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
s
and solutions to matrix equations.
The central algorithm is the efficient matrix-matrix multiplication, i.e., the computation of
for hierarchical matrices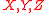 and a scalar factor
and a scalar factor  .
.
The algorithm requires the submatrices of the hierarchical matrices to be organized in a block tree structure and takes
advantage of the properties of factorized low-rank matrices to compute the updated in
in
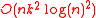 operations.
operations.
Taking advantage of the block structure, the inverse can be computed by using recursion to compute inverses and
Schur complementSchur complementIn linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
s of diagonal blocks and combining both using the matrix-matrix multiplication.
In a similar way, the LU decompositionLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
can be constructed using only recursion and multiplication.
Both operations also require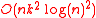 operations.
operations.
H2-matrices
In order to treat very large problems, the structure of hierarchical matrices can be improved:
H2-matrices
replace the general low-rank structure of the blocks by a hierarchical representation closely related to the
fast multipole methodFast Multipole MethodThe fast multipole method is a mathematical technique that was developed to speed up the calculation of long-ranged forces in the n-body problem...
in order to reduce the storage complexity to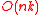 .
.
In the context of boundary integral operators, replacing the fixed rank by block-dependent ranks
by block-dependent ranks
leads to approximations that preserve the rate of convergence of the underlying boundary element method
at a complexity of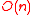
. -