Galerkin method
Encyclopedia
In mathematics
, in the area of numerical analysis
, Galerkin methods are a class of methods for converting a continuous operator problem (such as a differential equation
) to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a weak formulation
. Typically one then applies some constraints on the function space to characterize the space with a finite set of basis functions. Often when using a Galerkin method one also gives the name along with typical approximation methods used, such as Petrov–Galerkin method (after Alexander G. Petrov) or Ritz–Galerkin method (after Walther Ritz).
The approach is credited to the Russian mathematician Boris Galerkin
.
Examples of Galerkin methods are:
on a Hilbert space
,
, namely,
Here,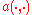
is a bilinear form (the exact requirements on 
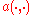will be specified later) and 
is a bounded linear functional on 
.
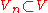of dimension n and solve the projected problem:
We call this the Galerkin equation. Notice that the equation has remained unchanged and only the spaces have changed.
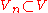, we can use 
as a test vector in the original equation. Subtracting the two, we get the Galerkin orthogonality relation for the error, 
which is the error between the solution of the original problem, 
, and the solution of the Galerkin equation,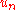 
Let
be a basis
for
. Then, it is sufficient to use these in turn for testing the Galerkin equation, i.e.: find 
such that
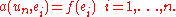
We expand
in respect to this basis,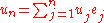 
and insert it into the equation above, to obtain
This previous equation is actually a linear system of equations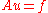
, where
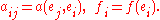
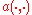is symmetric.
While this is not really a restriction of Galerkin methods, the application of the standard theory becomes much simpler. Furthermore, a Petrov-Galerkin method may be required in the nonsymmetric case.
The analysis of these methods proceeds in two steps. First, we will show that the Galerkin equation is a well-posed problem
in the sense of Hadamard and therefore admits a unique solution. In the second step, we study the quality of approximation of the Galerkin solution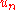
.
The analysis will mostly rest on two properties of the bilinear form, namely
By the Lax-Milgram theorem (see weak formulation
), these two conditions imply well-posedness of the original problem in weak formulation. All norms in the following sections will be norms for which the above inequalities hold (these norms are often called an energy norm).
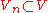, boundedness and ellipticity of the bilinear form apply to 
. Therefore, the well-posedness of the Galerkin problem is actually inherited from the well-posedness of the original problem.
between the original and the Galerkin solution admits the estimate
This means, that up to the constant
, the Galerkin solution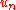 
is as close to the original solution
as any other vector in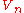 
. In particular, it will be sufficient to study approximation by spaces 
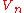, completely forgetting about the equation being solved.
by ellipticity and boundedness of the bilinear form (inequalities) and Galerkin orthogonality (equals sign in the middle), we have for arbitrary
:
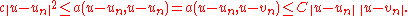
Dividing by
and taking the infimum over all possible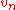 
yields the lemma.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Galerkin methods are a class of methods for converting a continuous operator problem (such as a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
) to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a weak formulation
Weak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
. Typically one then applies some constraints on the function space to characterize the space with a finite set of basis functions. Often when using a Galerkin method one also gives the name along with typical approximation methods used, such as Petrov–Galerkin method (after Alexander G. Petrov) or Ritz–Galerkin method (after Walther Ritz).
The approach is credited to the Russian mathematician Boris Galerkin
Boris Galerkin
Boris Grigoryevich Galerkin , born in Polozk, Belarus, Russian Empire was a Russian/Soviet mathematician and an engineer.-Early days:Galerkin was born on in Polotsk, Russian Empire, now part of Belarus. His parents owned a house in the town, but the homecraft they made did not bring enough money,...
.
Examples of Galerkin methods are:
- The Galerkin method of weighted residuals, the most common method of calculating the global stiffness matrix in the finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, - Boundary element methodBoundary element methodThe boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
for solving integral equations - Krylov subspace methods
A problem in weak formulation
Let us introduce Galerkin's method with an abstract problem posed as a weak formulationWeak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
,
, namely,
- find
such that for all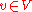 
, 
.
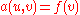Here,
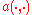is a bilinear form (the exact requirements on 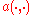will be specified later) and is a bounded linear functional on .Galerkin discretization
Choose a subspace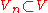 of dimension n and solve the projected problem:
- Find
such that for all 
, 
.
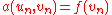We call this the Galerkin equation. Notice that the equation has remained unchanged and only the spaces have changed.
Galerkin orthogonality
The key property of the Galerkin approach is that the error is orthogonal to the chosen subspaces. Since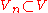, we can use as a test vector in the original equation. Subtracting the two, we get the Galerkin orthogonality relation for the error, which is the error between the solution of the original problem, , and the solution of the Galerkin equation, 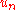Matrix form
Since the aim of Galerkin's method is the production of a linear system of equations, we build its matrix form, which can be used to compute the solution by a computer program.Let
be a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for
. Then, it is sufficient to use these in turn for testing the Galerkin equation, i.e.: find such that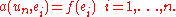We expand
in respect to this basis, 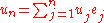and insert it into the equation above, to obtainThis previous equation is actually a linear system of equations
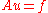, where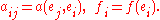Symmetry of the matrix
Due to the definition of the matrix entries, the matrix of the Galerkin equation is symmetric if and only if the bilinear form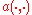 is symmetric.Analysis of Galerkin methods
Here, we will restrict ourselves to symmetric bilinear forms, that isWhile this is not really a restriction of Galerkin methods, the application of the standard theory becomes much simpler. Furthermore, a Petrov-Galerkin method may be required in the nonsymmetric case.
The analysis of these methods proceeds in two steps. First, we will show that the Galerkin equation is a well-posed problem
Well-posed problem
The mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
in the sense of Hadamard and therefore admits a unique solution. In the second step, we study the quality of approximation of the Galerkin solution
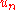.The analysis will mostly rest on two properties of the bilinear form, namely
- Boundedness: for all
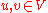holds
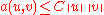for some constant 
- Ellipticity: for all
holds
for some constant 
By the Lax-Milgram theorem (see weak formulation
Weak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
), these two conditions imply well-posedness of the original problem in weak formulation. All norms in the following sections will be norms for which the above inequalities hold (these norms are often called an energy norm).
Well-posedness of the Galerkin equation
Since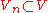, boundedness and ellipticity of the bilinear form apply to . Therefore, the well-posedness of the Galerkin problem is actually inherited from the well-posedness of the original problem.Quasi-best approximation (Céa's lemma)
The error between the original and the Galerkin solution admits the estimateThis means, that up to the constant
, the Galerkin solution 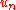is as close to the original solution
as any other vector in 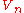. In particular, it will be sufficient to study approximation by spaces 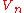, completely forgetting about the equation being solved.Proof
Since the proof is very simple and the basic principle behind all Galerkin methods, we include it here:by ellipticity and boundedness of the bilinear form (inequalities) and Galerkin orthogonality (equals sign in the middle), we have for arbitrary
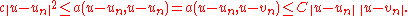
:Dividing by
and taking the infimum over all possible 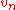yields the lemma.