Hereditarily countable set
Encyclopedia
In set theory
, a set is called hereditarily countable if it is a countable set
of hereditarily
countable sets. This inductive definition is in fact well-founded and can be expressed in the language of first-order
set theory. A set is hereditarily countable if and only if it is countable, and every element of its transitive closure
is countable. If the axiom of countable choice
holds, then a set is hereditarily countable if and only if its transitive closure is countable.
The class of all hereditarily countable sets can be proven to be a set from the axioms of Zermelo-Fraenkel set theory (ZF) without any form of the axiom of choice, and this set is designated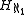
. The hereditarily countable sets form a model of Kripke–Platek set theory
with the axiom of infinity
(KPI), if the axiom of countable choice is assumed in the metatheory
.
If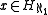
, then 
.
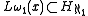More generally, a set is hereditarily of cardinality less than κ if and only it is of cardinality less than κ, and all its elements are hereditarily of cardinality less than κ; the class of all such sets can also be proven to be a set from the axioms of ZF, and is designated
. If the axiom of choice holds, then a set is hereditarily of cardinality less than κ if and only if its transitive closure is of cardinality less than κ.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a set is called hereditarily countable if it is a countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
of hereditarily
Hereditary property
In mathematics, a hereditary property is a property of an object, that inherits to all its subobjects, where the term subobject depends on the context. These properties are particularly considered in topology and graph theory.-In topology:...
countable sets. This inductive definition is in fact well-founded and can be expressed in the language of first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
set theory. A set is hereditarily countable if and only if it is countable, and every element of its transitive closure
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
is countable. If the axiom of countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
holds, then a set is hereditarily countable if and only if its transitive closure is countable.
The class of all hereditarily countable sets can be proven to be a set from the axioms of Zermelo-Fraenkel set theory (ZF) without any form of the axiom of choice, and this set is designated
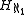. The hereditarily countable sets form a model of Kripke–Platek set theoryKripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
with the axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
(KPI), if the axiom of countable choice is assumed in the metatheory
Metatheory
A metatheory or meta-theory is a theory whose subject matter is some other theory. In other words it is a theory about a theory. Statements made in the metatheory about the theory are called metatheorems....
.
If
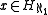, then 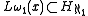.More generally, a set is hereditarily of cardinality less than κ if and only it is of cardinality less than κ, and all its elements are hereditarily of cardinality less than κ; the class of all such sets can also be proven to be a set from the axioms of ZF, and is designated
. If the axiom of choice holds, then a set is hereditarily of cardinality less than κ if and only if its transitive closure is of cardinality less than κ.External links
- "On Hereditarily Countable Sets" by Thomas JechThomas JechThomas J. Jech is a mathematician specializing in set theory who was at Penn State for more than 25 years. He was educated at Charles University and is now at the of the Academy of Sciences of the Czech Republic....